1T 2015 vår LØSNING

Oppgaven

Diskusjon av denne oppgaven

Vurderingsskjema

Sensorveiledning

Løsning laget av mattepratbruker LektorH

Oppgave 1

$$\begin{gathered} \frac{7,5\cdot {10}^{15}}{0,003} \\ =\frac{7,5}{3}\cdot {10}^{15+3} \\ =2,5\cdot {10}^{18} \end{gathered}$$

Oppgave 2

$\left[\begin{array}{r}x+6y=1\\ 2x+4y=-6\end{array}\right]$

$\left[\begin{array}{r}x=1-6y\\ 2(1-6y)+4y=-6\end{array}\right]$

$\left[\begin{array}{r}x=1-6y\\ 2-12y+4y=-6\end{array}\right]$

$\left[\begin{array}{r}y=1\end{array}\right]$

Innsatt i første likning gir det x=-5, dvs:

$x=-5\wedge y=1$

Oppgave 3

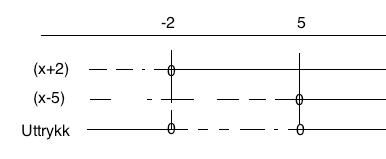
$x^2-3x-10>0$

Løser andregradslikningen: $$\begin{gathered} x^2-3x-10=0 \\ x=\frac{3\pm \sqrt{9+40}}{2} \\ x=\frac{3\pm 7}{2} \\ x=-2\vee x=5 \end{gathered}$$

Vi observerer at uttrykket skulle være større enn null: $x\in <\leftarrow ,-2>\cup <5,\to >$

Oppgave 4

a)

$$\begin{gathered} 4^{\frac{1}{2}}\cdot 8^0\cdot 2^{-1}\cdot \sqrt[4]{16} \\ =2\cdot 1\cdot 0,5\cdot 2 \\ =2 \end{gathered}$$

b)

$$\begin{gathered} \sqrt{18}\cdot \sqrt{2}+\frac{\sqrt{72}}{\sqrt{8}} \\ =\sqrt{18\cdot 2}+\sqrt{\frac{72}{8}} \\ =6+3=9 \end{gathered}$$

Oppgave 5

$$\begin{gathered} lg(x^2-0,9)=-1 \\ {10}^{lg(x^2-0,9)}={10}^{-1} \\ {x}^2-0,9=0,1 \\ {x}^2=1 \\ x=\pm 1 \end{gathered}$$

Vi kan ikke ta logaritmen til et negativt tall, og ma sjekke begge løsningene. I dette tilfellet kan begge løsninger brukes:

$x=-1\vee x=1$

Oppgave 6

$x^2+bx+16$

Vi registrerer at $16=4^2$. Da må b vare lik det dobbelte av 4, i følge 1. kvadratsetning.

$x^2+8x+16=(x+4{)}^2$

b er altså lik 8

Oppgave 7

$$\begin{gathered} 2x(x-2)-(x-2)(2x+1) \\ =2x^2-4x-(2x^2+x-4x-2) \\ =2x^2-4x-2x^2-x+4x+2 \\ =-x+2 \end{gathered}$$

Oppgave 8

$$\begin{gathered} \frac{x^2-12x+36}{2X^2-72} \\ =\frac{(x-6)(x-6)}{2(x+6)(x-6)} \\ =\frac{x-6}{2(x+6)} \end{gathered}$$

Oppgave 9

En rett linje har likningen :

y = ax + b

Stigningstall er: a = $\frac{\mathrm{\Delta }y}{\mathrm{\Delta }x}=\frac{4-2}{3-(-1)}=\frac{1}{2}$

Bruker x og y verdi i første punkt og finner b:

$$\begin{gathered} 2=\frac{1}{2}\cdot -1+b \\ b=\frac{5}{2} \end{gathered}$$

$y=\frac{1}{2}x+\frac{5}{2}$

Oppgave 10

a)

Bruker Pytagoras på trekant ABC og får:

AB = $\sqrt{2^2-1^2}=\sqrt{3}$

Bruker Pytagoras på trekant DEF og får:

DF = $\sqrt{1^2+1^2}=\sqrt{2}$

b)

u	sin u	cos u	tan u
${30}^{\circ }$	$\frac{1}{2}$	$\frac{\sqrt{3}}{2}$	$\frac{1}{\sqrt{3}}$
${45}^{\circ }$	$\frac{\sqrt{2}}{2}$	$\frac{\sqrt{2}}{2}$	1
${60}^{\circ }$	$\frac{\sqrt{3}}{2}$	$\frac{1}{2}$	$\sqrt{3}$

Oppgave 12

$f(x)=-2x^2+4x+6$

Oppgave 13

Jordens radius er r, og omkretsen er O.

$O=2\pi r$

Dersom vi forlenger tauet med 20 meter blir ny omkrets: O + 20. Vi må da finne tillhørende radius.

$r=\frac{O}{2\pi }$

Ny radius blir:

$r_{20}=\frac{O+20}{2\pi }=\frac{O}{2\pi }+\frac{10}{\pi }$

Tauet vil være ca. 3 meter over bakkenivå så det vil være mulig å gå under tauet.