Løsning del 2 utrinn Høst 13

Oppgave 1

a)

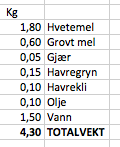
Ingredienser:

De veier 4,3 Kg, eller 4300 gram.

b)

Dersom vi deler alle mengden i oppskriften på 4, finner vi mengden for ett brød. Deretter ganger vi det med 5, siden vi skal lage fem brød. Det er det samme som å gange alle mengdene med $\frac{5}{4}$:

Hvetemel: $\frac{5}{4}\cdot 1,8kg=2,25kg$

Grovt mel:$\frac{5}{4}\cdot 600g=750g$

Havregryn:$\frac{5}{4}\cdot 150g=188g$

Havrekli:$\frac{5}{4}\cdot 100g=125g$

Olje:$\frac{5}{4}\cdot 100g=125g$

Vann$\frac{5}{4}\cdot 1,5liter=1,88liter$

Oppgave 2

a)

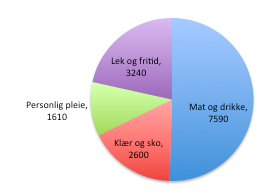
Oversikt over månedlige utgifter:

b)

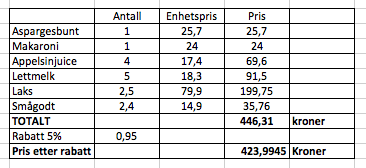
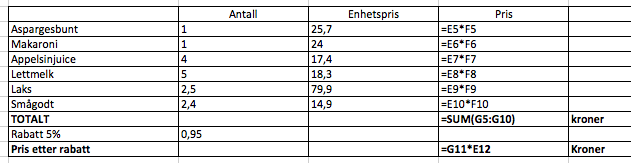
Hun må betale 424 kroner for varene.

Formelbruk:

c)

Merverdiavgiften er på 15%

Oppgave 3

a)

40 liter tilsvarer $40d{m}^3$.

$1m^3=1000d{m}^3$

For å få en kubikkmeter ved trenger man $\frac{1000}{40}=25$ sekker.

Bjørkeved: $25\cdot 75kr=1875$ kroner.

Granved: $25\cdot 60kr=1500$ kroner.

b)

Energi per krone:

Bjørkeved: $\frac{2715kWh}{1875kr}=1,448$ kWh/ krone

Granved: $\frac{2150kWh}{1500kr}=1,433$ kwh/krone

På papiret gir bjørkeveden marginalt mere energi per krone, i praksis vil man neppe merke forskjell.

Oppgave 4

a)

Varmetap gjennom vindu:

$$\begin{gathered} V=10,5\cdot A\cdot T\cdot (I-U) \\ V=10,5\cdot (1,1m\cdot 0,8m)\cdot 24\cdot (20-1) \\ V=4213,44kJ \end{gathered}$$

b)

Det betyr at energien går utenfra og inn. Det skjer dersom U er større enn I.

Oppgave 5

a)

Hver av de fire sideflatene er to rettvinklede trekanter med hypotenus 17,0 cm. Det ene katetet er 5,0 cm, det andre h. Bruker pytagoras:

$h=\sqrt{17,0^2-5,0^2}=16,2$ Høyden h i den likebeinte trekanten er 16,2 cm

Arealet av en trekant blir: $A=\frac{16,2cm\cdot 10,0cm}{2}=81,2c{m}^2$

Pyramiden består av fire slike trekanter: Overflate: $O=4\cdot 81,2c{m}^2=325,0c{m}^2$

Om vi også tar med kvadratet i bunnen blir den totale overflaten $425,0c{m}^2$

b)

For å finne H bruker vi pytagoras en gang til:

$H=\sqrt{16,2^2-5,0^2}=15,4$

Høyden H i pyramiden er 15,4 centimeter.

Volum av pyramide:

$V=\frac{1}{3}\cdot A\cdot H=\frac{1}{3}\cdot 100,0c{m}^2\cdot 15,4cm=513,6c{m}^3$

Volumet av pyramidekortet er $513,6c{m}^3$.

c)

Her kan vi bruke formlikhet. Kaller halve lengden i det kvadratiske hullet for x:

$$\begin{gathered} \frac{15,4}{5,4}=\frac{5}{x} \\ x=1,75 \end{gathered}$$

Sidekantene i det kvadratiske hullet må være 3,5 centimeter, for at "rammen" skal ligge 10 centimeter over grunnflaten.

Oppgave 6

a)

b)

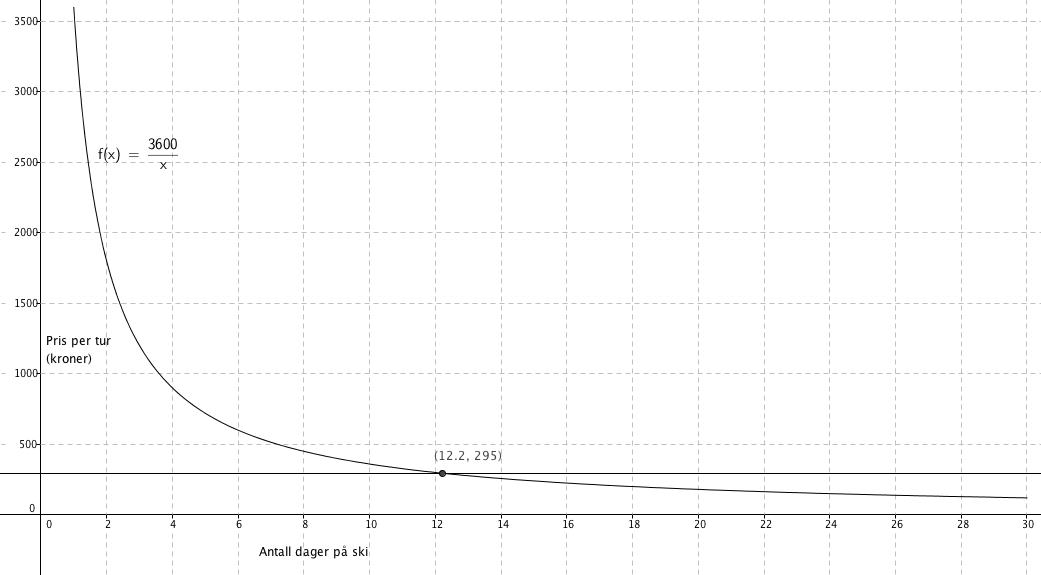
Man ser fra figuren i a, at dersom Kari er på ski 14 dager eller mere vil det lønne seg med sesongkort.

Oppgave 7

a)

Kombinasjoner som gir syv øyner på to terninger er (1,6), (2,5), (3,4), (4,3), (5,2) og (6,1), altså seks utfall.

P(sum øyne syv)=$\frac{6}{36}=\frac{1}{6}$

b)

Mulige primtall er 3, 5, 7 og 11.

Tilsvarende opptelling som i a gir 14 gunstige utfall.

P(primtall)=$\frac{14}{36}=\frac{7}{18}$

Oppgave 8

a)

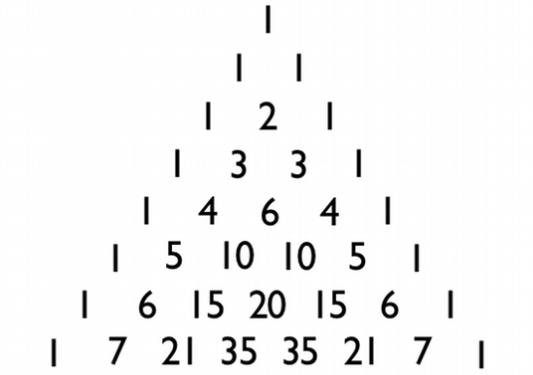
Sum: $$\begin{gathered} 1 \\ 1+1=2 \\ 1+2+1=3 \\ 1+3+3+1=8 \\ 1+4+6+4+1=16 \\ 1+5+10+10+5+1=32 \\ 1+6+15+20+15+6+1=64 \\ 1+7+21+35+35+21+7+1=128 \end{gathered}$$

Som potenser med grunntall 2:

$2{,}^0,2^1,2^2,2^3,2^4,2^5,2^{6}og{2}^7$

b)

$$\left[\begin{array}{c}21+x=y\\ 2x+y=126\end{array}\right]$$

Oppgave 9

a)

$$\begin{gathered} V_1+V_2+V_3+V_4+V_5+V_6+V_7+V_8= \\ {a}^{2}b+a^3+a{b}^2+a^{2}b+a{b}^2+b^3+a^{2}b+a{b}^2= \\ {a}^3+3a^{2}b+3a{b}^2+b^3 \end{gathered}$$

b)

$$\begin{gathered} (a+b{)}^0=1 \\ (a+b{)}^1=a+b \\ (a+b{)}^2=a^2+2ab+b^2 \\ (a+b{)}^3=a^3+3a^{2}b+3a{b}^2+b^3 \end{gathered}$$

Koeffisienten foran variablene a og b er dem man finner på radene i Pascals talltrekant.