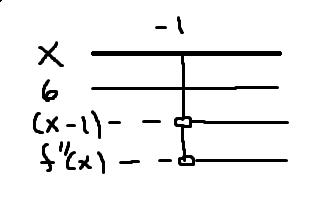S2 2015 høst LØSNING: Forskjell mellom sideversjoner
| Linje 87: | Linje 87: | ||
$\frac{a_n}{n+1}=\frac{n^3+1}{n+1}=\frac{(n+1)(n^2-n+1)}{n+1}=n^2-n+1$ | $\frac{a_n}{n+1}=\frac{n^3+1}{n+1}=\frac{(n+1)(n^2-n+1)}{n+1}=n^2-n+1$ | ||
Alternativt kan du si at $(n+1)$ er en av faktorene til $n^3+1$ siden (-1)^3+1=0$ | Alternativt kan du si at $(n+1)$ er en av faktorene til $n^3+1$ siden $(-1)^3+1=0$ | ||
==Oppgave 7== | ==Oppgave 7== | ||
Sideversjonen fra 9. des. 2015 kl. 14:55
DEL 1
Oppgave 1
a)
$f(x)=x^3+2x \\ f'(x)=3x^2+2$
b)
$g(x)=3e^{2x-1} \\ g'(x)=3e^{2x-1} \cdot (2x-1)'=6e^{2x-1}$
c)
$h(x)=x^2 \cdot e^x \\ h'(x)=2xe^x+x^2e^x=xe^x(2+x)$
Oppgave 2
a)
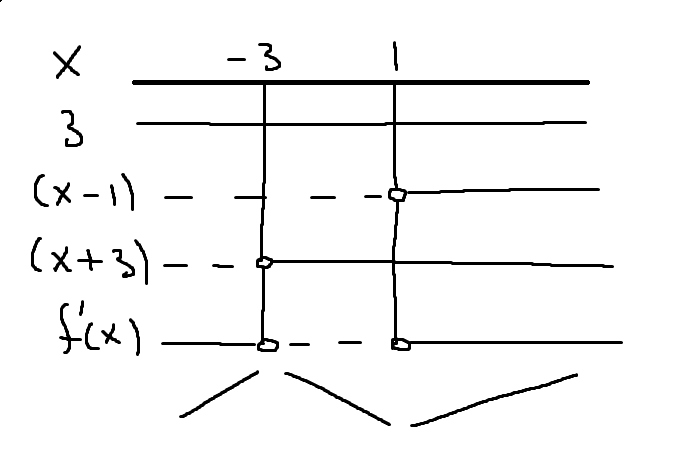
$f(x)=x^3+3x^2-9x \\ f'(x)=3x^2+6x-9=3(x^2+2x-3)=3(x-1)(x+3)$
Alternativt kan $f'(x)$ faktoriseres med ABC-formelen
Toppunkt: $T=(-3,f(-3))=(-3,-27+27+27)=(-3,27)$
Bunnpunkt: $B=(1,f(1))=(1,1+3-9)=(1,-5)$
b)
$ f ' ' (x)=6x+6=6(x+1) $
$6(x+1)=0$
$x=-1$
Vendepunkt: $V=(-1,f(-1))=(-1,-1+3+9)=(-1,11)$
c)
Utifra nullpunkter, ekstremalpunkter, vendepunkt og fortegnslinja til $f'(x)$ skal man kunne klare å lage en god skisse.
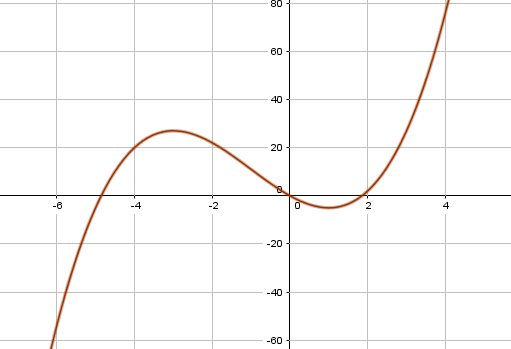
Oppgave 3
a)
$x^3-ax^2+2ax-8$ er alltid delelig med $(x-2)$ siden $2^3-2^2a+4a-8=0$
b)
Forkorter med polynomdivisjon.
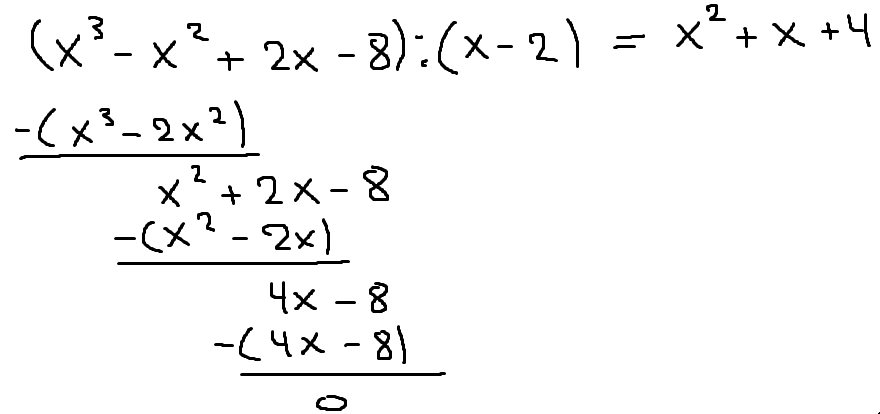
Oppgave 4
$ (1); \ x+2y-z=2 \\ (2); \ 2x-y+z=3 \\ (3); \ 3x-2y+2z=2 $
Her kan man bruke innsetingsmetoden eller adderingsmetoden. Jeg bruker adderingsmetoden. Fra $(1)$ og $(2)$.
$(4); \ (x+2y-z)+(2x-y+z)=3x+y=5$
Fra $(2)$ og $(3)$.
$-2(2x-y+z)+(3x-2y+2z)=-x=-2\cdot3+2=-4$
$x=4$
Fra (4). $y=5-3 \cdot 4=-7$
Fra (1). $z=x+2y-2=4+2\cdot-7-2=-12 $
$x=4 \ , \ y=-7 \ \ , \ z=-12 $
Oppgave 5
a)
$1+\frac{1}{2}+\frac{1}{4}+...+\frac{1}{2^{n-1}}$
Dette er en geometrisk rekke siden den følger mønsteret $a_n=(\frac{1}{2})^{n-1}$
b)
$S_n=1+\frac{1}{2}+\frac{1}{4}+...+\frac{1}{2^{n-1}}$
$S_n=\frac{a_1}{1-k}=\frac{1}{1-\frac{1}{2}}=2$
Oppgave 6
a)
$a_n=n^3+1 \\ a_1=2 \\ a_2=9 \\ a_3=28 \\ a_4=65$
b)
$\frac{a_1}{2}=1 \\ \frac{a_2}{3}=3 \\ \frac{a_3}{4}=7 \\ \frac{a_4}{5}=13$
c)
$\frac{a_n}{n+1}=\frac{n^3+1}{n+1}=\frac{(n+1)(n^2-n+1)}{n+1}=n^2-n+1$
Alternativt kan du si at $(n+1)$ er en av faktorene til $n^3+1$ siden $(-1)^3+1=0$