S1 2015 høst LØSNING: Forskjell mellom sideversjoner
| Linje 103: | Linje 103: | ||
===b)=== | ===b)=== | ||
[[File:s1-h2015-6b.png]] | |||
==Oppgave 7== | ==Oppgave 7== | ||
Sideversjonen fra 23. des. 2015 kl. 17:06
DEL EN
Oppgave 1
a)
$2x^2-3x=0 \\x(2x-3)= 0 \\ x=0 \vee x = \frac 32$
b)
$2^{3x+1} = 4^{17} \\ 2^{3x+1} = 2^{34} \\ 3x+1 = 34 \\ x = 11$
c)
$lg(2x+2) = 3 + lg2 \\ lg(2x+2) = lg(1000\cdot 2) \\ 2x= 1998 \\ x= 999$
Oppgave 2
a)
$\frac{8a^3(a^{-1}b)^2}{(2ab)^2}= \\ \frac{2^3a^3a^{-2}b^2}{2^2a^2b^2} = \\ 2^{3-2}a^{3-2-2}b^{2-2} = \\ 2a^{-1} = \\ \frac2a$
b)
$(x+y)(x-y) + (y+x) (y-x) - (x+y)(x-y)= \\ y^2-x^2$
Oppgave 3
<math> \left[ \begin{align*} 2x^2+x+y=7\\ 3x+y=-5 \end{align*}\right] </math>
<math> \left[ \begin{align*} 2x^2+x+y=7\\ y=-5 -3x \end{align*}\right] </math>
<math> \left[ \begin{align*} 2x^2+x+(-5-3x)=7\\ y=-5 - 3x \end{align*}\right] </math>
Løser første likning og får to x verdier:
$2x^2-2x- 12 =0 \\ x= \frac{2 \pm \sqrt{4+96}}{4} \\ x=-2 \vee x= 3$
Det gir følgende y verdier:
x =-2: y= - 5+6 =1
x = 3: y = - 14
Løsning; $(-2,1) \wedge (3, -14)$
Oppgave 4
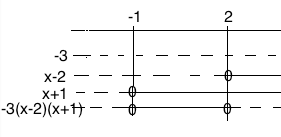
$-3(x-2)(x+1)<0$
Fortegnsskjema:
$x \in < \leftarrow, -1 > \cup <2, \rightarrow>$
Oppgave 5
a)
$f(x)=x^3-x^2-x+3 \\ f(0)= 3 \\ f(2)= 8-4-2+3= 5$
Gjennomsnittlig vekstfart i intervallet blir da $\frac{f(2)-f(0)}{2} = 1$
b)
$f´(x) =3x^2-2x-1 \\ f´(0) = -1$
Siden den deriverte er negativ for x = 0, synker grafen til f.
c)
$f´(x)=0 \\ 3x^2-2x-1=0 \\ x= \frac{2 \pm \sqrt{4+12}}{6} \\ x= 1 \vee x= - \frac 13$
Fra b har vi at grafen synker for x = 0
X=1 gir da et minimum og x= $-\frac13$ gir maksimum.
$f(1) =1 -1 -1 +3= 2\\ f(-\frac 13)= 3,19$
Oppgave 6
a)
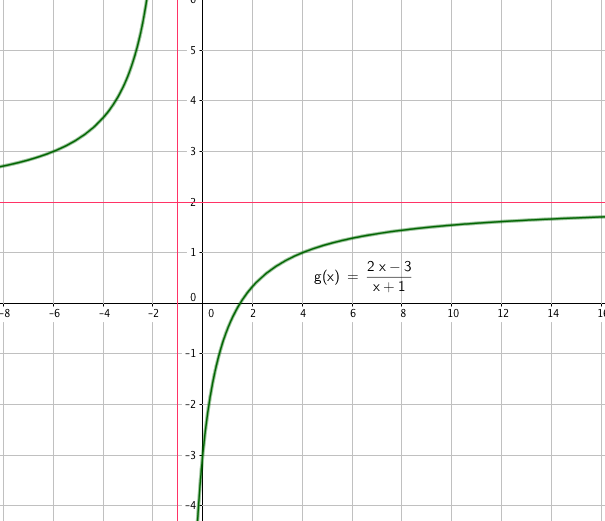
Skjæring med y akse:
$g(0) = -3$
Skjæring med y aksen er i -3, altså (0, -3).
Skjæring med x akse:
$g(x)= 0 \\ 2x-3 = 0 \\ x= \frac 32$,
altså $(\frac32,0)$
b)
Oppgave 7
a)
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
b)
Fra a gir det 10 mulige kombinasjoner.