1P 2015 høst LØSNING

• Diskusjon av denne oppgaven på matteprat
• mer diskusjon av denne oppgaven på matteprat
• Løsningsforslag del 1 av jøgge

• oppgaven (bedre versjon kommer snart)
• oppgaven (bedre versjon)

Løsningsforslag (pdf) fra bruker joes. Send gjerne en melding hvis du har kommentarer til løsningsforslaget. På forhånd, takk.

Oppgave 1

a)

$$\begin{gathered} \frac{0,4}{1,0}=\frac{2,4}{x} \\ 0,4x=2,4 \\ x=\frac{2,4}{0,4} \\ x=6 \end{gathered}$$

Man bør ikke spise mere enn 6 gram salt daglig.

b)

Dersom 100g inneholder 0,8g vil 300g inneholde tre ganger så mye:

$0,8g\cdot 3=2,4g$ salt

En porsjon pizza inneholder 2,4 gram salt.

c)

$2,4\cdot 0,4g=0,96g$ natrium.

$$\begin{gathered} 0,96:2,4= \\ 9,6:24=0,4 \end{gathered}$$

Dvs 40% av dagsbehovet.

Oppgave 2

a)

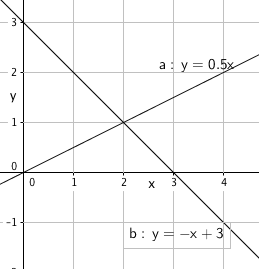
Ved avlesning: skjæringspunkt i (2, 1).

b)

$$\begin{gathered} f(x)=g(x) \\ \frac{1}{2}x=-x+3 \\ x=-2x+6 \\ 3x=6 \\ x=2 \end{gathered}$$

f(2)= 1

Skjæringspunkt mellom f og g : (2,1)

Oppgave 3

Reallønn = nominell lønn $\cdot \frac{100}{indeks}$

$$\begin{gathered} 360000=450000\cdot \frac{100}{x} \\ x=\frac{45000000}{360000}=125 \end{gathered}$$

Konsumprisindeksen var på 125 det året.

Oppgave 4

Dersom omvendt proporsjonale størrelser: $$\begin{gathered} y=\frac{k}{x} \\ xy=k \end{gathered}$$

20kr / is $\cdot$ 200 is = 4000 kr

25kr / is $\cdot$ 160 is = 4000 kr

40kr / is $\cdot$ 100 is = 4000 kr

Pris og antall er omvendt proporsjonale størrelser.