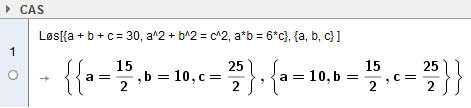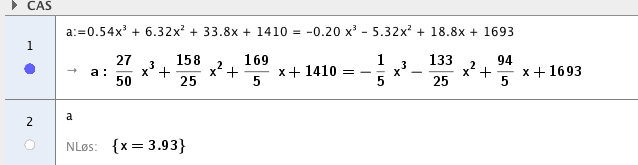1T eksempeloppgave 2015 vår LØSNING

Oppgave 1

a)

$$\begin{gathered} 8,20\cdot {10}^9\cdot 1,50\cdot {10}^{-3}= \\ 12,30\cdot {10}^{9-3}= \\ 1,23\cdot {10}^7 \end{gathered}$$

b)

$\frac{(a^2{)}^4\cdot (\frac{b}{a}{)}^2}{a^3\cdot b^{-2}}=\frac{a^8\cdot \frac{b^2}{a^2}}{a^3{b}^{-2}}=a^{8-5}{b}^4=a^3{b}^4$

Oppgave 2

a)

$$\begin{gathered} (a+b{)}^2-(a-b{)}^2= \\ {a}^2+2ab+b^2-(a^2-2ab+b^2)= \\ {a}^2+2ab+b^2-a^2+2ab-b^2= \\ 4ab \end{gathered}$$

b)

$$\begin{gathered} \frac{2x+6}{2x^2-18} \\ =\frac{2(x+3)}{2(x+3)(x-3) \\ =\frac{1}{x-3}} \end{gathered}$$

Oppgave 3

a)

$$\begin{gathered} g(x)=\frac{1}{3}{x}^3-x^2-3x+4D_g=\text{R} \\ {g}^{\prime }(x)=x^2-2x-3 \\ {g}^{\prime }(1)=1-2-3=-4 \end{gathered}$$

Den momentane vekstfarten i x = 1 er -4.

b)

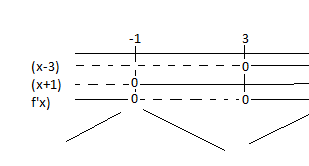
$$\begin{gathered} g^{\prime }(x)=0 \\ {x}^2-2x-3=0 \\ x=-1\vee x=3 \end{gathered}$$

Fortegnsskjema:

$$\begin{gathered} g(-1)=-\frac{1}{3}-1+3+4=5\frac{2}{3} \\ g(3)=9-9-9+4=-5 \end{gathered}$$

Maksimumspunkt i $(-1,\frac{17}{3})$

Minimumspunkt i $(3,-5)$

Oppgave 4

a)

Et kvadrat med omkrets 16 har sider lik 4 og et areal på 16.

En sirkel med omkrets 16 har radius $\frac{8}{\pi }$. Arealet blir da

$$\begin{gathered} A=\pi r^2 \\ A=\pi (\frac{8}{\pi }{)}^2 \\ A=\frac{64}{\pi } \end{gathered}$$

som er et større areal enn 16. Sirkelen har størst areal.

b)

$$\begin{gathered} A=\frac{(a+b)}{2}\cdot h \\ h=\frac{2A}{(a+b)} \end{gathered}$$

c)

De parallelle sidene er x og x + 2 cm. lange.

$$\begin{gathered} 18=\frac{x+x+2}{2}\cdot 3 \\ 3x+3=18 \\ x=5 \end{gathered}$$

Den ene siden er 5 cm lang, den andre 7 cm lang.

Oppgave 5

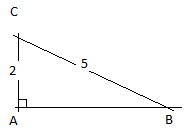
a)

b)

$$\begin{gathered} A=\frac{1}{2}abSinC \\ sin{140}^{\circ }>sin{30}^{\circ } \end{gathered}$$

$\mathrm{△}ABC$ har størst areal.

Oppgave 6

a)

$$\begin{gathered} y=ax+b \\ a=\frac{\mathrm{\Delta }y}{\mathrm{\Delta }x}=\frac{4-2}{2-1}=2 \\ y=2x+b \\ 2=2\cdot 1+b \\ b=0 \\ y=2x \end{gathered}$$

b)

$$\begin{gathered} f(x)=x^2+4 \\ {f}^{\prime }x)=\underset{\mathrm{\Delta }x\to 0}{lim}\frac{f(x+\mathrm{\Delta }x)-f(x)}{\mathrm{\Delta }x} \\ =\underset{\mathrm{\Delta }x\to 0}{lim}\frac{(x+\mathrm{\Delta }x{)}^2+4-x^2-4}{\mathrm{\Delta }x} \\ =\underset{\mathrm{\Delta }x\to 0}{lim}\frac{x^2+2x\mathrm{\Delta }x+(\mathrm{\Delta }x{)}^2+4-x^2-4}{\mathrm{\Delta }x} \\ =\underset{\mathrm{\Delta }x\to 0}{lim}\frac{\mathrm{\Delta }x(2x+\mathrm{\Delta }x)}{\mathrm{\Delta }x} \\ =\underset{\mathrm{\Delta }x\to 0}{lim}2x+\mathrm{\Delta }x=2x \end{gathered}$$

Oppgave 7

a)

Sannsynlighet for to rosa sokker:

$P(to-rosa)=\frac{2}{10}\cdot \frac{1}{9}=\frac{1}{45}$

Det er 1/45 dels sjanse for at hun trekker to rosa sokker.

b)

Sannsynligheten for en rosa og en i en annen farge:

$P(enrosaogenannenfarge)=\frac{2}{10}\cdot \frac{8}{9}+\frac{8}{10}\cdot \frac{2}{9}=\frac{16}{45}$

Det er 16/45 sjanse for å trekke en rosa sokk, i kombinasjon med en annen.

Oppgave 8

a)

$$\begin{gathered} -\frac{1}{4}x+2=2x-\frac{5}{2} \\ -x+8=8x-10 \\ -9x=-18 \\ x=2 \end{gathered}$$

b)

$\left[\begin{array}{r}x+y=7\\ 3x-2y=-4\end{array}\right]$

$\left[\begin{array}{r}x=7-y\\ 3(7-y)-2y=-4\end{array}\right]$

$$\begin{gathered} 21-3y-2y=-4 \\ -5y=-25 \\ y=5 \end{gathered}$$

Innsatt i likning en gir det x = 2, dvs: $x=2\wedge y=5$

c)

$-2x^2+9x+5\le 0$

Løser

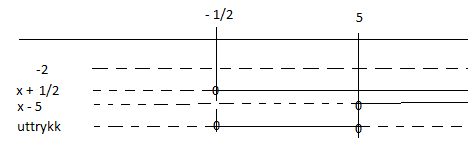
$$\begin{gathered} -2x^2+9x+5=0 \\ x=-\frac{1}{2}\vee x=5 \end{gathered}$$

Uttrykk: $-2x^2+9x+5=-2(x+\frac{1}{2})(x-5)$

I følge ulikheten skal uttrykket være mindre eller lik null, dvs:

$x\in <\leftarrow ,-\frac{1}{2}]\cup [5,\to >$

Oppgave 9

Skjærer y- aksen i (0. 1)

f(0) = 1, dvs c = 1

Ett nullpunkt betyr at uttrykket under rottegnet i ABC formelen er null:

$$\begin{gathered} b^2-4\cdot 4\cdot 1=0 \\ b=\pm 4 \end{gathered}$$

To funksjoner oppfyller kravene:

$f(x)=4x^2+4x+1\wedge f(x)=4x^2-4x+1$

Oppgave 10

a)

Finner arealet av OAB og trekker fra arealet av de mindre trekantene OQP, QBM og MAP.

Areal $trianglePQM$ $$\begin{gathered} A=16-(\frac{x^2}{2}+\frac{(8-x)2}{2}+\frac{(4-x)4}{2}) \\ A=16-\frac{x^2}{2}-8+x-8+2x \\ A=-\frac{x^2}{2}+3x \end{gathered}$$

Som skulle vises. (x kan ikke være mindre enn null, eller større enn fire).

b)

$$\begin{gathered} T^{\prime }(x)=-x+3 \\ {T}^{\prime }(x)=0 \\ x=3 \end{gathered}$$

Vi ser av fortegnet til andregradsleddet i T at x = 3 gir et maksimumspunkt. Arealtet av trekanten PQM er altså størst når x = 3.

T(3) = 4,5

Oppgave 1

a)

a + b + c = 30 : Sidene er a, b og c. Summen av disse er omkretsen, som er 30.

$a^2+b^2=c^2$: Trekanten er rettvinklet og vi kan anvende Pytagoras.

ab er det dobbelte av trekantens areal. gh = 6c, er også det dobbelte av trekantens areal. Derfor er ab = 6c.

b)

Oppgave 2

a)

	Gjør lekser	Gjør ikke lekser	Totalt
Fornøyd med karakter	16	4	20
Ikke fornøyd med karakter	1	9	10
Totalt	17	13	30

b)

P (gjør lekser til hver time) = $\frac{17}{30}$

c)

P( fornøyd | gjør lekser) = $\frac{16}{17}$

Oppgave 3

Vinkel B er:

${180}^{\circ }-94,9^{\circ }-69,7^{\circ }=15,4^{\circ }$

Bruker så sinussettningen i cas:

Avstanden mellom A og B er 94,1 meter.

Oppgave 4

Vi lar CAS gjøre utregningene, men her er framgangsmåten: Vi bruker cosinussetningen og tar for eksempel ${24}^2={20}^2+{14}^2-2\ast 20\ast 14\ast CosA$ Da vil vi finne $CosA=\frac{{20}^2+{14}^2-{24}^2}{2\ast 20\ast 14}$ og da er $\mathrm{\angle }A\approx 87,7^{\circ }$ Og til sist bruker vi arealsetningen $T_{\mathrm{△}ABC}=\frac{1}{2}\ast 20\ast 14\ast SinA\approx 140m^2$

Oppgave 5

Først lager vi en funksjon for arealet av ABC. Da kombinerer vi f(x) som gir oss høyden i trekanten, og som er punktet C på grafen, med x som er distansen fra A = Origio til B.

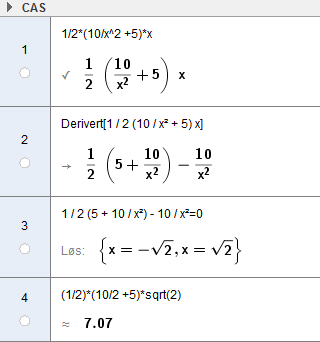
$T_{\mathrm{△}ABC}=\frac{1}{2}\ast (\frac{10}{x^2}+5)\ast x$

Dette gjør vi i CAS. Så lar vi CAS derivere den nye funksjonen vår, og så lar vi CAS finne nullpunktene til den deriverte. $-\sqrt{2}$ kan vi stryke ut, fordi den originale funksjonen vår kun er definert for x>0. Da må $\sqrt{2}$ være løsningen.

Da finner vi at arealet må være 7,07.

Oppgave 6

a)

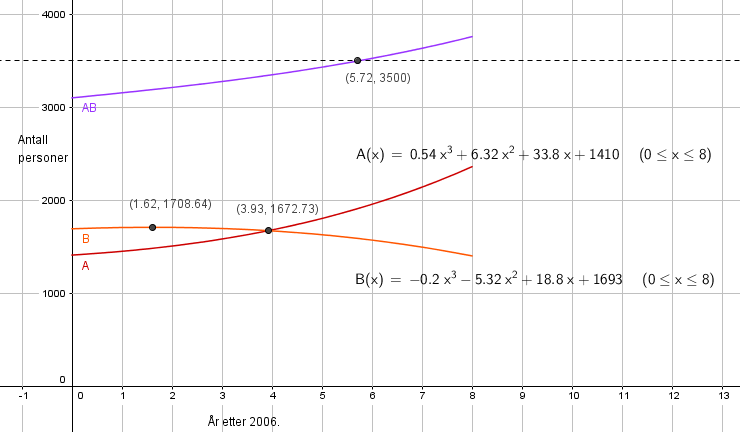
Tolker det slik at 1 på x-aksen er 31.12.2007, altså ett år etter at 2006 var slutt.

1): Bruker komandoen "Ekstremalpunkt" og finner maksimum for 1,62, det vil si andre halvdel av 2008.

2): Folketallet var likt i A og B i slutten av 2010. Da var det ca 1635 innbyggere hvert av stedene.

3):Fra Figuren ser man at det skjer i tredje kvartal i 2012 (5,72).

b)

c)

$$\begin{gathered} B´(x)=-0,60x^2-10,64x+18,8x\in [0,8] \\ B´(0)=1,62 \end{gathered}$$

Folketallet er størst i andre halvdel av 2007.

Oppgave 7

$$\begin{gathered} 8=2h+2r+\pi r \\ h=\frac{8-2r-\pi r}{2} \\ A=2rh+\frac{1}{2}\pi r^2 \\ A=8r-2r^2-\frac{1}{2}\pi r^2 \end{gathered}$$

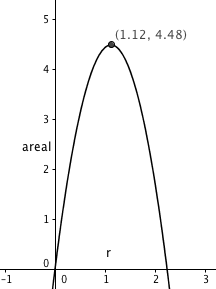
Setter uttrykket for A inn i graftegneren:

Arealet er størst, 4,5 $m^2$ når r = 1,1 m.