2P 2016 høst LØSNING

Oppgave 1

26,3 millioner = 26 300 000 = $2,63\cdot {10}^7$

$16,5\cdot {10}^{-8}=1,65\cdot {10}^{-9}$

Oppgave 2

$\frac{3,5\cdot {10}^8}{7,0\cdot {10}^5\cdot 0,5\cdot {10}^6}=\frac{3,5}{7\cdot 0,5}\cdot {10}^{8-5-6}=1,0\cdot {10}^{-3}$

Oppgave 3

$\frac{135}{135+115}=\frac{135}{250}=\frac{270}{500}=\frac{540}{1000}=\frac{54}{100}=54$ %.

Det er 54% jenter på skolen.

Oppgave 4

Butikk A: $1,1\cdot 0,9$

Butikk B: $0,9\cdot 1,1$

Prisen er den samme i begge butikkene ( Rekkefølgen av faktorene har ikke betydning).

Oppgave 5

$1024=2^{10}$

$\frac{2^{10}}{2^7}=2^{10-7}=2^3=8$

Etter 7 uker har du 8 kroner igjen.

Oppgave 6

a)

Synker med ca. 2500 dyr på 5 år dvs et stigningstall på -500.

$f(t)=-500t+8500$

b)

$f(8)=-500\cdot 8+8500=4500$

I 2018 vil det være ca 4500 dyr igjen, i følge modellen.

c)

$$\begin{gathered} f(t)=0 \\ -500t+8500=0 \\ -500t=-8500 \\ t=17 \end{gathered}$$

I følge modellen vil det ikke være flere dyr igjen i 2017.

Oppgave 7

a)

Klasse (ant. kunder)	Frekvens	Relativ frekvens	Kumulativ frekvens
[0,50>	1	0,05	1
[50, 100>	5	0,25	6
[100, 150>	8	0,40	14
[150, 200>	6	0,30	20

Siden den relative frekvensen i første interval er 0,05, er det det samme som 1 av 20. Derfor frekvens 1 i første interval. Kummulativ i andre interval er 6, da må frekvensen i dette intervallet være 5. 8/20 er 0,40 og kummulativ frekv. i interval tre blir da 14.

b)

Det mangler en verdi i intervallet [ 0, 50>. Dette kan for eksempel være 42.

Det mangler to verdier i intervallet [ 150, 200>, Disse kan begge være 170.

Oppgave 8

a)

$V(x)=250000\cdot 0,9^x$

250000 - kjøpesum bil

0,9 - vekstfaktor som forteller at den taper seg i verdi med 10% per år (1 - 0,1 = 0,9).

b)

$V(1)=250000\cdot 0,9=225000$

Bilen vil i følge modellen ha en verdi på ca. 225 000 kroner.

Oppgave 9

a)

Forutsetter at datamateriealet fordeler seg jevnt innen hver klasse.

Gjennomsnitt: $\frac{2,5\cdot 4+7,7\cdot 12+12,5\cdot 10+22,5\cdot 4}{30}=10,5$

Gjennomsnittet er 10,5 poeng.

b)

Går man etter gjennomsnittet var han i den nedre halvdelen.

Median er nr. 15 og 16. Vi ser at begge disse verdiene befinner seg i mengden [ 5, 10>. Så Per bør holde seg til medianen når han legger fram sin påstand.

Oppgave 10

A = 3 Hun går, dvs. fjerner seg sakte fra hjemmet.

B = 2 Løper, gir brattere stigningstall enn A. Venter. Går tilbake. Nærmer seg saktere enn Eline i A som løper tilbake

C = 4 Padling i motvind gir konstant fart. vinden stillner, farten og derved også avstanden til hjemmet øker raskere. Hun kom aldri tilbake....

D = 1 Beveger seg fram og tilbake uten pause.

Oppgave 3

a)

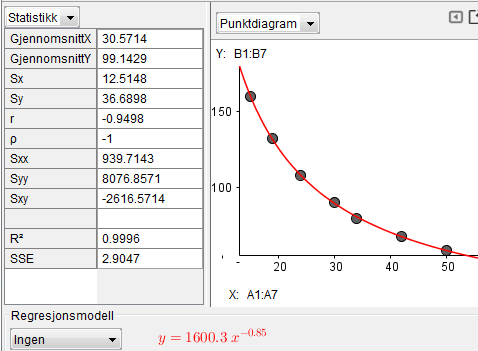
Kvadratet av regresjonskoefisienten: $R^2=0,9996$, altså nesten 1,0 betyr at tilnærmingen er god. Du kan også se at punktene ligger på grafen.

b)

c)

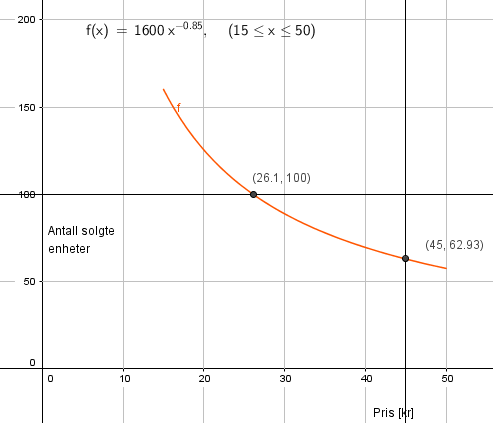
Dersom prisen er 45 kroner selges det 63 enheter. Se graf i b.

d)

Når det selges 100 enheter er prisen 26 kroner. Se graf i b.

e)

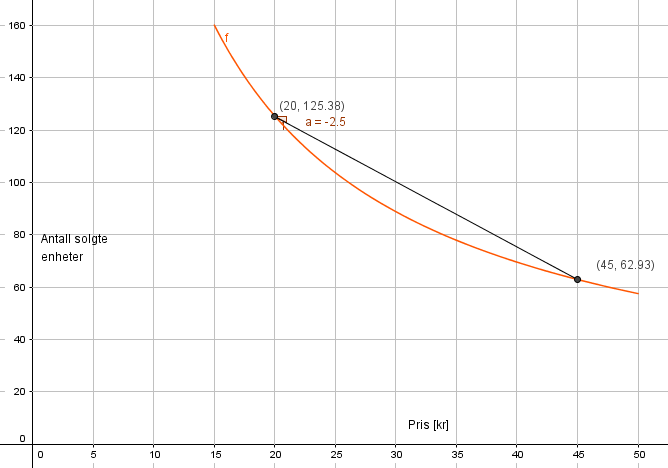
Dersom man øker prisen fra 20 til maks 45 kroner, vil antall solgte enheter i gjennomsnitt minke med 2,5 enheter for hver krone man øker prisen.

Oppgave 7

b)

Figuren består av et "hode" med to "ører". Hodet har høyde n og bredde n+1. Antall klosser i hodet blir da $n(n+1)=n^2+n$. Ørene er kvadrater med sider (n-1). V får da $n^2+n+2(n-1{)}^2=n^2+n+2(n^2-2n+1)=3n^2-3n+3$.

Dersom du synes at det er vannskelig å finne denne sammenhengen legger du figurnummer og tilhørende antall ruter inn i regnearket på geogebra og utfører regresjon.