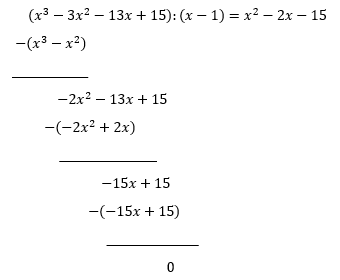S2 2018 vår LØSNING

oppgave som pdf

Diskusjon av denne oppgaven på matteprat

Løsning laget av mattepratbruker Tommy O.

DEL 1

Oppgave 1

a)

$$\begin{gathered} f(x)=2x^3-4x+1 \\ {f}^{\prime }(x)=6x^2-4 \end{gathered}$$

b)

$g(x)=\frac{x}{e^x}$

$g^{\prime }(x)=\frac{1\cdot e^x-x\cdot e^x}{(e^x{)}^2}=\frac{e^x(1-x)}{(e^x)(e^x)}=\frac{1-x}{e^x}$

c)

$$\begin{gathered} h(x)=ln(x^2+4x) \\ g(u)=ln(u),u=x^2+4x \\ {h}^{\prime }(x)=g^{\prime }(u)\cdot u^{\prime }(x)=\frac{1}{u}\cdot u^{\prime }=\frac{2x+4}{x^2+4x} \end{gathered}$$

Oppgave 2

$$\begin{gathered} I5x+y+2z=0 \\ II2x+3y+z=3 \\ III3x+2y-z=-3 \end{gathered}$$

Legger sammen likning II og III.

$$\begin{gathered} 2x+3x+3y+2y+z-z=3-3 \\ 5x+5y=0 \\ x+y=0 \\ x=-y \end{gathered}$$

Setter inn $x=-y$ i likning I.

$$\begin{gathered} 5\cdot (-y)+y+2z=0 \\ -4y+2z=0 \\ 2z=4y \\ z=2y \end{gathered}$$

Setter inn $z=2y$ og $x=-y$ i likning II.

$$\begin{gathered} 2\cdot (-y)+3y+2y=3 \\ 3y=3 \\ y=1 \end{gathered}$$

$x=-y=-1$

$z=2y=2\cdot 1=2$

Løsning: $x=-1,y=1,z=2$

Oppgave 3

a)

$P(x)=x^3-3x^2-13x+15$

$P(1)=1^3-3\cdot 1^2-13\cdot 1+15=1-3-13+15=0$

x=1 er et nullpunkt, så P(x) er delelig med (x-1).

b)

Utfører polynomdivisjon for å faktorisere P(x)

Resten faktoriseres: $x^2-2x-15=(x^2-5x+3x+(-5)\cdot 3)=(x-5)(x+3)$. Bruk andregradsformelen ved behov.

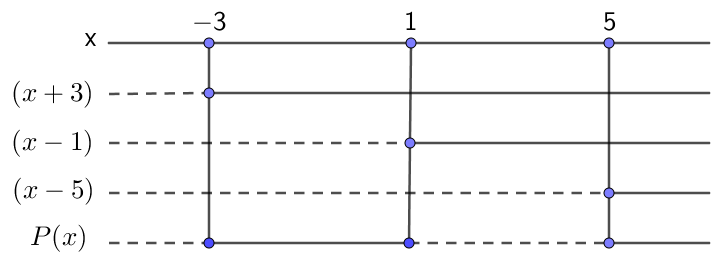
Vi har $P(x)=(x-5)(x-1)(x+3)$. Bruker fortegnsskjema for å løse ulikheten.

$P(x)>0$ når $-3<x<1$ og $x>5$.

Løsningen kan også skrives som $x\in ⟨-3,1⟩$ og $x\in ⟨5,\to ⟩$

Oppgave 4

a)

Differansen, d, mellom to ledd i en aritmetisk rekke er konstant. Finner d:

$$\begin{gathered} a_4=a_1+d+d+d \\ 14=2+3d \\ 3d=12 \\ d=4 \end{gathered}$$

n	1	2	3	4	n
$a_n$	2	6	10	14
Formel	$2+4\cdot 0$	$2+4\cdot 1$	$2+4\cdot 2$	$2+4\cdot 3$	$2+4\cdot (n-1)=4n-2$

$a_n=4n-2$

b)

Summen av en aritmetisk rekke er gitt ved:

$S_n=\frac{a_1+a_n}{2}\cdot n$

Finner $a_{100}$:

$a_{100}=4\cdot 100-2=398$

Regner ut summen av de 100 første leddene i vår rekke:

$S_{100}=\frac{2+398}{2}\cdot 100=200\cdot 100=20000$

Oppgave 5

a)

Dersom $-1<k<1$ i en geometrisk tallfølge $a_n=a_1{k}^{n-1}$ sier vi at den konvergerer. I slike tilfeller er $S_n=\frac{a_1}{1-k}$ når n går mot uendelig.

Her har vi $a_n=3\cdot (\frac{1}{4}{)}^{n-1}$. Siden $-1<k<1$, så konvergerer rekken.

Regner ut summen av rekken når n går mot uendelig:

$S_n=\frac{3}{1-(\frac{1}{4})}=\frac{3}{\frac{3}{4}}=\frac{3\cdot 4}{3}=4$

b)

$0,242424...=0,24+0,0024+0,000024+...=\frac{24}{100}+\frac{24}{{100}^2}+\frac{24}{{100}^3}+...$

Dette er en geometrisk rekke hvor

$a_n=\frac{24}{100}\cdot (\frac{1}{100}{)}^{n-1}$

Siden $-1<k<1$, konvergerer rekken. Summen av denne rekken når n går mot uendelig er:

$S_n=\frac{\frac{24}{100}}{1-\frac{1}{100}}=\frac{\frac{24}{100}}{\frac{99}{100}}=\frac{24}{99}$

Det betyr at $0,242424...$ kan skrives som $\frac{24}{99}$

Oppgave 6

a)

$f(x)=\frac{6}{1+e^{-x}}$

$f^{\prime }(x)=\frac{0\cdot (1+e^{-x})-6\cdot (-e^{-x})}{(1+e^{-x}{)}^2}=\frac{6e^{-x}}{1+2e^{-x}+e^{-2x}}$

Alle potenser av $e$ er positive (og større enn 0). Både telleren og nevneren til $f^{\prime }(x)$ er altså positive. En brøk med positiv teller og nevner har alltid positiv verdi. Altså er den deriverte positiv (og større enn 0) for alle verdier av x. Det vil si at $f(x)$ er strengt voksende.

DEL 2

Oppgave 1

a)

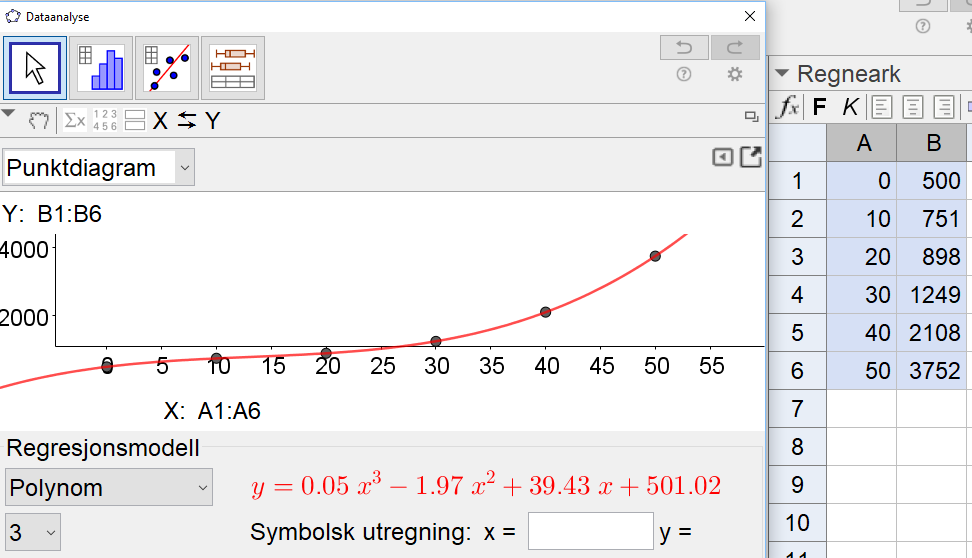
Bruker Geogebra til å utføre en regresjonsanalyse på punktene i tabellen. Velger polynomfunksjon av 3. grad som modell for kostnadene, h(x). Se skjermbildet under.

Jeg har funnet en modell for kostnaden, $h(x)=0,05x^3-1.97x^2+39,43x+501,02$

Inntekten er 80 kroner per enhet, og kan uttrykkes som $I(x)=80x$.

For å finne en modell for overskuddet, O(x), bruker jeg CAS i Geogebra, og regner ut O(x)=I(x)-h(x). Se skjermbildet under.

Jeg har dermed vist at funksjonen $O(x)=-0,05x^2+2,0x^2+41x-501$ (noe avrundet) er en god modell for det daglig overskuddet til bedriften ved produksjon av x enheter.