1T 2019 vår LØSNING

oppgaven som pdf

Diskusjon av oppgaven på matteprat

Løsningsforslag laget av Marius Nilsen ved Bergen Private Gymnas

Løsningsforslag laget av Ole Henrik Morgenstierne

DEL EN

Oppgave 1

$\frac{4,5\cdot {10}^{12}}{900}=\frac{4,5}{9}\cdot \frac{{10}^{12}}{{10}^2}=0,5\cdot {10}^{10}=5,0\cdot {10}^9$

Oppgave 3

$$\begin{gathered} \frac{x^2}{x^2-4}+\frac{3}{x-2}+\frac{1}{x+2} \\ =\frac{x^2}{(x+2)(x-2)}+\frac{3(x+2)}{(x+2)(x-2)}+\frac{1(x-2)}{(x+2)(x-2)} \\ =\frac{x^2+3x+6+x-2}{(x+2)(x-2)} \\ =\frac{x^2+4x+4}{(x+2)(x-2)} \\ =\frac{(x+2)(x+2)}{(x+2)(x-2)} \\ =\frac{x+2}{x-2} \end{gathered}$$

Oppgave 4

I denne type oppgave kan det lønne seg å prøve å faktorisere grunntallene for å minimalisere antallet grunntall. $16=2^4,9=3^2$ osv.

$$\begin{gathered} 4^2\cdot 2^{-3}\cdot {27}^{\frac{1}{3}}\cdot {64}^{-\frac{2}{3}} \\ =(2^2{)}^2\cdot 2^{-3}\cdot (3^3{)}^{\frac{1}{3}}\cdot (2^6{)}^{-\frac{2}{3}} \\ =2^4\cdot 2^{-3}\cdot 2^{-4}\cdot 3^1 \\ =3\cdot 2^{-3} \\ =\frac{3}{2^3}=\frac{3}{8} \end{gathered}$$

Oppgave 5

Dette er en likebeint trekant. Normalen fra vinkelen dannet av sidene som begge er 5 vil dele grunnlinja i to like store linjestykker som hver har lengde 3. Bruker Pytagoras og ser at høyden i trekanten er 4, ($5^2-3^2=h^2$).

Definisjonen på tangens til en vinke er motstående katet dividert på hosliggende katet, altså:

$\tan v=\frac{4}{3}$

Oppgave 6

Det hjelper å huske at $lg1=0$ og at $lg10=1$

$$\begin{gathered} lg100+lg1+lg\sqrt{10}+lg0,001 \\ =lg{10}^2+0+lg{10}^{\frac{1}{2}}+lg{10}^{-3} \\ =2lg10+\frac{1}{2}lg10-3lg10 \\ =2+\frac{1}{2}-3 \\ =-\frac{1}{2} \end{gathered}$$

Oppgave 7

$$\begin{gathered} lg({10}^x\cdot {10}^{2x}=6 \\ lg({10}^{(x+2x)}=6 \\ lg({10}^{3x})=6 \\ 3x\cdot lg10=6 \\ 3x\cdot 1=6 \\ x=2 \end{gathered}$$

a)

1) $\sqrt{48}=\sqrt{2\cdot 2\cdot 2\cdot 2\cdot 3}=\sqrt{16}\sqrt{3}=4\sqrt{3}$

2) $\sqrt{75}=\sqrt{3\cdot 5\cdot 5}=5\sqrt{3}$

b)

Vi vet at definisjonen på cosinus i en rettvinklet trekant er hosliggende katet delt på hypotenus. Fra ungdomskolen vet vi at i en 30 - 60 - 90 trekant er det korteste katetet halvparten så lang som hypotenusen. Dersom vi lager en 30-60-90 trekant med hypotenusene lengde lik 1 får vi:

$cos60=\frac{\frac{1}{2}}{1}=\frac{1}{2}$

c)

Vi bruker Cosinussetningen for å finne BC:

$$\begin{gathered} B{C}^2=(\sqrt{75}{)}^2+(\sqrt{48}{)}^2-2\cdot \sqrt{75}\cdot \sqrt{48}\cdot \cos 60 \\ B{C}^2=75+48-2\cdot \frac{1}{2}\cdot \sqrt{75}\cdot \sqrt{48} \end{gathered}$$

Så benytter vi resultatene fra oppgave a:

$$\begin{gathered} B{C}^2=123-5\sqrt{3}\cdot 4\sqrt{3} \\ B{C}^2=123-60 \\ B{C}^2=63 \\ BC=\sqrt{63} \\ BC=\sqrt{9\cdot 7} \\ BC=3\sqrt{7} \end{gathered}$$

Oppgave 12

Arealet er gitt: A = 12. Arealsetningen gir $$\begin{gathered} A=\frac{1}{2}\cdot a\cdot b\cdot \sin c \\ \sin c=\frac{2A}{a\cdot b} \\ \sin {120}^{\circ }=\frac{2\cdot 12}{2\sqrt{3}\cdot 8}=\frac{24}{16\sqrt{3}} \\ {120}^{\circ }=\frac{24\sqrt{3}}{16\sqrt{3}\sqrt{3}}=\frac{24\sqrt{3}}{48}=\frac{\sqrt{3}}{2} \end{gathered}$$

Oppgave 13

Vi deler figuren opp.

Vi har tre fjerdedeler av en sirkel med radius 3a

Vi har en linje med lengden 2a og en linje med lengden 3a. For å finne lengden av den tredje linjen, den som går på skrå i koordinatsystemet, bruker vi Pytagoras. Den endrer seg 3a i x retning og 4a i y retning:

$\sqrt{(3a{)}^2+(4a{)}^2}=\sqrt{25a^2}=5a$

Omkretsen blir da:

Oppgave 14

Den deriverte av p i null lik null stemmer for A og D. Den deriverte av p i -1 skal vare negativ, stemmer bare for A. Derfor er A grafen til p.

Vi ser at graf E har en konstant stigning lik -2 (altså synker den med to for hver enhet av x) og er den eneste som passer til betingelsene til q. Altså viser E grafen til funksjonen q.

Når vi beveger oss fra -2 til 0 på x aksen har vi beveget oss to enheter. Dersom den gjennomsnittlige veksten skal bli 3 må endringen på y aksen være 6 ( $\frac{\mathrm{\Delta }y}{\mathrm{\Delta }x}=\frac{6}{2}=3$ ). Den eneste grafen som passer til kravene er F. Altså viser F grafen til r.

Begge tangentene har stigningstall -8 når x=-2 og x=2. Det betyr at funksjonen avtar. Det passer kun med B. B er grafen til s.

DEL TO

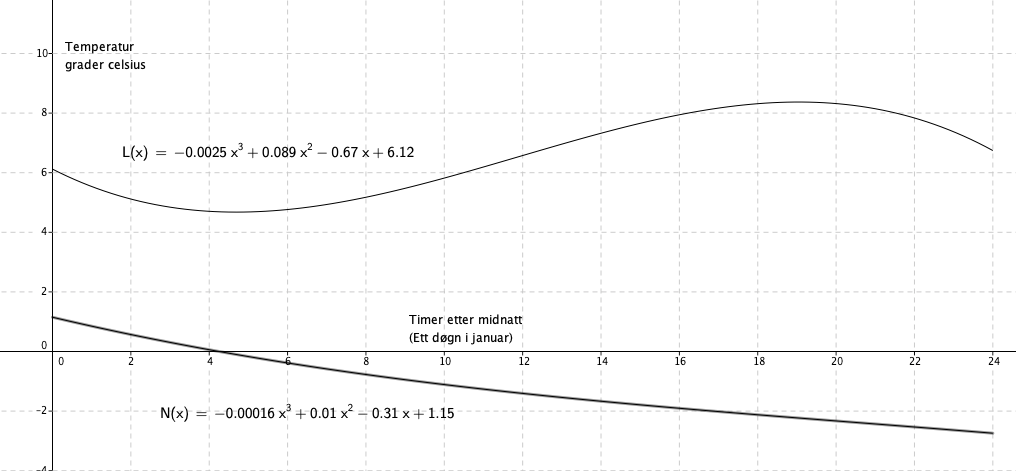
a)

L er temperatur på Lindesnes

N er temperatur på Nordkapp

b)

[[File:1t-v19-2-1-b.png]

Når klokken er 8 på morgen øker temperaturen på Lindesnes med 0,27 grader per time. På Nordkapp synker den med