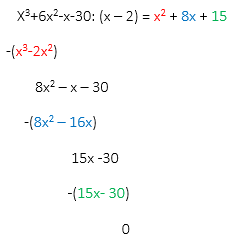R1 2019 høst LØSNING: Forskjell mellom sideversjoner
| Linje 63: | Linje 63: | ||
Areal av skravert område blir da | Areal av skravert område blir da | ||
$A_{skravert} = \frac 14 \pi \cdot2^2$ | $A_{skravert} = \frac 14 \pi \cdot2^2 - x \cdot \sqrt{4-x^2} = \pi - x \sqrt{4-x^2}$ | ||
===b)=== | ===b)=== | ||
Sideversjonen fra 23. des. 2019 kl. 06:17
Diskusjon av oppgaven på matteprat
Løsningsforslag del 2 fra Kristian Saug
Løsningsforslag (pdf) fra joes
Løsningsforslag fra Svein Arneson
DEL EN
Oppgave 1
a)
$ f(x)=x^4-2x+ln(x) \\ f'(x)= 4x^3-2+ \frac 1x$
b)
$ g(x)= x^7e^x \\ g'(x) = 7x^6e^x + x^7e^x = e^xx^6(7+x) $
c)
$h(x)= \frac{ln(2x)}{x^2} \\ h'(x) = \frac{\frac{1}{2x} \cdot 2 \cdot x^2-2 \cdot x \cdot ln(2x)}{x^4} \\ h'(x)= \frac{1- 2 ln(2x)}{x^3}$
Oppgave 2
$4(ln(a \cdot b^3))-3(ln(a\cdot b^2))-ln(\frac ab) \\ 4 ln(a) + 12 ln(b) - 3ln(a) - 6 ln(b) - ln (a) + ln(b) = 7 ln (b)$
Oppgave 3
a)
Dersom P(x) skal deles på (x-2) og gå opp. må P(x) = 0, dvs. P(2) = 0
$P(2) = 0 \\ 2^3+ 6 \cdot 2^2 + k\cdot 2 -30 =0 \\ 8+24+2k-30=0 \\ k=-1$
b)
Bruker så ABC formel på svaret og får:
$ x^2 + 8x + 15 = 0 \\ x = \frac{-8 \pm \sqrt{64-4 \cdot 1 \cdot 15}}{2} \\ x = \frac{-8 \pm 2}{2} \\ x = -5 \vee x =-3$
Faktorisert form:
$x^3 +6x^2 - x -30 = (x-2)(x+3)(x+5)$
c)
Oppgave 4
Oppgave 5
Oppgave 6
a)
Diagonal i rektangelet er alltid 2. Arealet er alltid $ A = x \cdot \sqrt{4-x^2} $. Brukte pytagoras for å finne lengden av OC.
Areal av skravert område blir da
$A_{skravert} = \frac 14 \pi \cdot2^2 - x \cdot \sqrt{4-x^2} = \pi - x \sqrt{4-x^2}$
b)
Oppgave 7
a)
CB er like lang som EB fordi begge linjestykker tangerer samme sirkelsektor ( i C og E).
b)
Begge trekantene har en felles vinkel i A. Begge trekanten har en vinkel på 90 grader (i C og E). Trekantene er derfor formlike.
Bruker formlikhet:
$\frac{c-a}{r} = \frac{b}{c} \\ r = \frac{a(c-a)}{b} $
c)
Trekanten ABC har areal: $A= \frac {a \cdot b}{2}$
Fra figuren ser vi at trekantene CDB og ADB utgjør trekanten ABC
Areal CDB: $\frac{r \cdot a}{2}$
Areal: ADB: $\frac{c \cdot r}{2}$
Kombinerer:
$\frac{r \cdot a}{2}+ \frac{c \cdot r}{2}=\frac {a \cdot b}{2} \\ra + rc = ab \\ r(a+c) =ab$
d)
$a \cdot b = (a+c) \cdot r \\ ab =(a+c) \cdot \frac{a(c+a)}{b} \\ ab^2 = (a^2+ac)(c-a) \\ ab^2= a^2c - a^3 + ac^2- a^2c \\ ab^2 = - a^3+ ac^2 \\ a^2 + b^2 = c^2$