S1 2020 høst LØSNING: Forskjell mellom sideversjoner
| Linje 69: | Linje 69: | ||
Setter $P(to\,ulike) < \frac{1}{2}$ | Setter $P(to\,ulike) < \frac{1}{2}$ | ||
$\frac{4x}{x^2+3x+2} < \frac{1}{2} \\ 8x < x^2+3x+2 \\ -x^2+5x-2 < 0 \\ x^2-5x+2 > 0 \\ x>\frac{5\pm\sqrt{25-4\cdot 1 \cdot 2}}{2} \\ x_1> \frac{5+\sqrt{17}}{2} \vee x_2>\frac{5 | $\frac{4x}{x^2+3x+2} < \frac{1}{2} \\ 8x < x^2+3x+2 \\ -x^2+5x-2 < 0 \\ x^2-5x+2 > 0 \\ x>\frac{5\pm\sqrt{25-4\cdot 1 \cdot 2}}{2} \\ x_1> \frac{5+\sqrt{17}}{2} \vee x_2>\frac{5-\sqrt{17}}{2}$ | ||
Velger den positive løsningen, $x_1$. Vi vet at $\sqrt{17} > 4$, siden $\sqrt{16}=4$. | Velger den positive løsningen, $x_1$. Vi vet at $\sqrt{17} > 4$, siden $\sqrt{16}=4$. | ||
Sideversjonen fra 5. des. 2020 kl. 17:40
Diskusjon av denne oppgaven på matteprat
Løsningsforslag laget av Marius Nilsen ved Bergen Private Gymnas
DEL 1
Oppgave 1
a)
$2(3x+2)=2x(x+2)+4 \\ 6x+4 = 2x^2+4x+4 \\ -2x^2+2x=0 \quad |:(-2)\\ x^2-x = 0 \\ x(x-1)=0 \\ x=0 \vee x=1 $
b)
$3^x\cdot 3^2=\frac{1}{3^5} \\ 3^{x+2}=3^{-5} \\ x+2=-5 \\ x=-7$
c)
$lg(3x-2)=2lgx \\ lg(3x-2)=lg(x^2) \\ 10^{lg(3x-2)}=10^{lg(x^2)} \\ 3x-2 = x^2 \\ -x^2+3x-2=0 \quad | :(-1)\\ x^2-3x+2=0 \\ (x-1)(x-2)=0 \\ x=1 \vee x=2$
Oppgave 2
a)
$\frac{4a^3(a^{-2}b^3)^2}{(2^{-1})^{-2}ab^4} \\ =\frac{4a^3\cdot a^{-4}\cdot b^6}{2^2\cdot ab^4} \\ = a^{3-4-1}\cdot b^{6-4} \\ = a^{-2}\cdot b^{2} \\ = (\frac{b}{a})^2 $
b)
$\frac{1}{x-1}-\frac{2x}{x^2-1}+1 \\ = \frac{x+1}{(x+1)(x-1)}-\frac{2x}{(x+1)(x-1)}+\frac{(x+1)(x-1)}{(x+1)(x-1)} \\ = \frac{x+1-2x+(x^2-1)}{(x+1)(x-1)} \\ = \frac{x^2-x}{(x+1)(x-1)} \\ = \frac{x(x-1)}{(x+1)(x-1)} \\ = \frac{x}{x+1}$
Oppgave 3
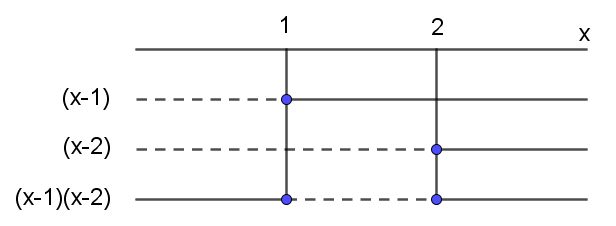
$x^2-3x+2\leq 0 \\ (x-1)(x-2)\leq 0$
Nullpunkter: $x=1$ og $x=2$
$x^2-3x+2\leq 0$ når $x\in [1,2]$
Oppgave 4
Vi lar $x$ være antall gullmedaljer, og $y$ være antall sølvmedaljer.
$I \quad x+y=16 \\ II \quad 7x+5y=102$
$I \quad y=16-x$
$II \quad 7x+5(16-x)=102 \\ \quad \quad 7x+80-5x=102 \\ \quad \quad 2x=102-80 \\ \quad \quad x=\frac{22}{2}=11$
Norge tok 11 gullmedaljer i vinter-OL i 2014.
Oppgave 5
a)
$P(to \, like)=P((B\cap B)\cup(R\cap R))= \frac{2}{4}\cdot \frac{1}{3}+\frac{2}{4}\cdot \frac{1}{3} = \frac{2}{12}+\frac{2}{12}=\frac{4}{12}=\frac{1}{3}$
Sannsynligheten for at Mia må ta oppvasken dersom de følger dette forslaget er $\frac{1}{3}$.
b)
La $x$ være antall røde kuler.
$P(to\, ulike)=P((B\cap R)\cup(R\cap B)) \\ = \frac{2}{2+x}\cdot \frac{x}{2+x-1} + \frac{x}{2+x} \cdot \frac{2}{2+x-1} \\ = \frac{2x}{(2+x)(1+x)}\cdot 2 \\ = \frac{4x}{x^2+2x+x+2} \\ = \frac{4x}{x^2+3x+2}$
Setter $P(to\,ulike) < \frac{1}{2}$
$\frac{4x}{x^2+3x+2} < \frac{1}{2} \\ 8x < x^2+3x+2 \\ -x^2+5x-2 < 0 \\ x^2-5x+2 > 0 \\ x>\frac{5\pm\sqrt{25-4\cdot 1 \cdot 2}}{2} \\ x_1> \frac{5+\sqrt{17}}{2} \vee x_2>\frac{5-\sqrt{17}}{2}$
Velger den positive løsningen, $x_1$. Vi vet at $\sqrt{17} > 4$, siden $\sqrt{16}=4$.
$x_1 > \frac{5+4}{2} \\ x_1 > 4,5$
Det må ligge flere enn 5 røde kuler i krukken, dersom sannsynligheten for at de to kulene som trekkes har ulik farge, er mindre enn 50 %.