1T 2021 høst LK20 LØSNING

Diskusjon av denne oppgaven på matteprat

DEL 1

Oppgave 1

Vet at stigningstallet for begge linjene er det samme, nemlig -2, siden linjene er parallelle.

Bruker ettpunktsformelen, hvor $x_1=5,y_1=-6,a=-2$

$y-y_1=a(x-x_1)$

$y-(-6)=-2(x-5)$

$y+6=-2x+10$

$y=-2x+10-6$

$y=-2x+4$ er likningen for linjen m.

Oppgave 2

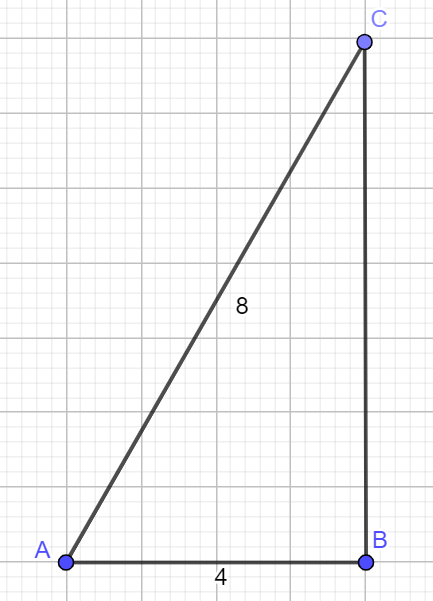
Tegner en hjelpetrekant.

Vet at $cosA=sinA=\frac{AB}{AC}=\frac{1}{2}$ og siden $AB=4$, har vi $AC=8$

Oppgave 3

Skal løse likningen $x^3+2x^2-7x+4=0$

Ser at x=1 er en løsning til likningen. Sjekker at det stemmer:

$1^3+2\cdot 1^2-7\cdot 1+4=1+2-7+4=0$

Det stemmer at x=1 er en løsning, og dermed er (x-1) en faktor. Bruker polynomdivisjon for å faktorisere resten av uttrykket.

$(x^3+2x^2-7x+4):(x-1)=x^2+3x-4$

$-(x^3-x^2)$

_____________________________

$3x^2-7x+4$

$-(3x^2-3x)$

_____________________________

$-4x+4$

$-(-4x+4)$

_____________________________

$0$

Faktoriserer $x^2+3x-4=(x+4)(x-1)$

Faktoriserer hele uttrykket $x^3+2x^2-7x+4=(x+4)(x-1)(x-1)$

Tredjegradslikningen har to løsninger: $x=-4$ og $x=1$

Oppgave 4

Fra likning II har vi at $y=-2-x$

Setter dette inn i likning I:

$x^2+2x-(-2-x)=-1$

$x^2+2x+2+x=-1$

$x^2+3x+3=0$

Bruker andregradsformelen:

$x=\frac{-3\pm \sqrt{3^2-4\cdot 1\cdot 3}}{2\cdot 1}$

$x=\frac{-3\pm \sqrt{-3}}{2}$

Vi får et negativt tall under kvadratroten, så denne likningen har ingen løsning. Derfor har heller ikke likningssystemet noen løsning.