2P 2022 vår K06 LØSNING: Forskjell mellom sideversjoner
| Linje 183: | Linje 183: | ||
===a)=== | ===a)=== | ||
[[File: | Jeg tegner figur 5 ved å følge mønsteret, og finner 65 prikker i figur nr. 5. | ||
[[File: 2P_V22_LK06_del1_6a2.png | 800 px]] | |||
===b)=== | ===b)=== | ||
| Linje 201: | Linje 205: | ||
| 8 | | 8 | ||
| 21 | | 21 | ||
| | | 40 | ||
| | | 65 | ||
| | | | ||
|- | |- | ||
Sideversjonen fra 26. mai 2022 kl. 11:55
Diskusjon av denne oppgaven på matteprat
DEL 1
Oppgave 1
a)
Skriver tallene i stigende rekkefølge:
2 2 4 4 5 5 5 6 6 10
Medianen gjennomsnittet av de to midterste tallene, som begge er 5. Medianen er altså $5$.
Gjennomsnitt: $\frac{2+2+4+4+5+5+5+6+6+10}{10}=\frac{49}{10}=4,9$
Typetallet er det tallet som forekommer flest ganger, nemlig $5$.
Variasjonsbredden er differansen mellom det høyeste og det laveste tallet: $10-2 = 8$
b)
For å finne relativ frekvens for fem fjellturer, tar vi antall forekomster av 5 fjellturer, og deler på antall år med fjellturer:
$\frac{3}{10}=0,3$.
Det forteller oss at 30% av årene, har Sebastian gått 5 fjellturer.
For å finne kumulativ frekvens, legger vi sammen antall forekomster av 5 eller færre fjellturer i året:
$2+2+3 = 7$
Det forteller oss at 7 av årene, har Sebastian gått 5 eller færre fjellturer i året.
Oppgave 2
$\frac{5\cdot 10^6+1,5\cdot 10^7}{2,5\cdot 10^{-6}}$
$ = \frac{5\cdot 10^6+15\cdot 10^6}{2,5\cdot 10^{-6}}$
$ = \frac{20\cdot 10^6}{2,5\cdot 10^{-6}}$
$ = 8\cdot 10^{6-(-6)}$
$ = 8\cdot 10^{12}$
Oppgave 3
a)
Finner 5 % av 600 000 kr:
10 % av 600 000 kr er 60 000 kr. 5 % av 600 000 kr er derfor 30 000 kr.
Verdien av båten om ett år vil være:
600 000 kr - 30 000 kr = 570 000 kr.
b)
Eirik tror at båtens verdi synker lineært med 30 000 kr per år. Til sammen 30 000 kr * 5 = 150 000 kr, som ville gi båten en pris på 450 000 kr om 5 år.
Det kan ikke stemme at båtens verdi synker like mye hvert år, fordi båtens verdi synker eksponentielt (det er en prosentvis nedgang). Det første året synker båtens verdi med 5 % av 600 000 kr, som er 30 000 kr. Det andre året er båten verdt 570 000 kr, og båtens verdi vi synke med 5 % av 570 000 kr, som er mindre enn 30 000 kr. Båtens verdi synker altså med et mindre beløp for verdt år.
Oppgave 4
a)
$K(x)=ax+b$
Vi har punktene (8,54) og (16,58) på grafen.
Finner stigningstallet a: $\frac{58-54}{16-8}=\frac{4}{8}=\frac{1}{2}$
Stigningstallet forteller oss at kartlaven vokser med en halv mm i diameter per år. Jeg antar at det er snakk om ett individ av kartlav.
Finner konstantleddet b: $54-\frac{1}{2}\cdot 8 = 54 - 4 = 50$
Konstantleddet forteller oss at den observerte kartlaven hadde en diameter på 50 mm ved første observasjon.
b)
I løpet av 200 år øker diameteren med kartlaven med $\frac{1}{2} mm/ år \cdot 200\, år = 100 \, mm$, det vil si $10\, cm$.
Oppgave 5
| Antall krabber | Klassemidtpunkt (m) | Antall dager (f) | m*f |
|---|---|---|---|
| [0,20> | 10 | 5 | 50 |
| [20,30> | 25 | 10 | 250 |
| [30,40> | 35 | 10 | 350 |
| [40,60> | 50 | 15 | 750 |
| [60,100> | 80 | 20 | 1600 |
| Sum | 60 | 3000 |
Gjennomsnitt: $\frac{3000}{60} = 50$
Det var i gjennomsnitt 50 krabber per dag i teinene.
b)
Den 30. dagen (av 60) ligger 5 dager "inn" i klassen [40,60> krabber. Vi antar at antall krabber funnet de 15 dagene i klassen [40,60> er jevnt fordelt i klassen. Tar klassebredden delt på antall dager i klassen, ganger 5:
Medianen vi være $\frac{20}{15}\cdot 5 = 20\cdot \frac{1}{3} \approx 7$ krabber "inn" i klassen, altså 47. Stian kan altså ha rett.
c)
Det er ikke sikkert at antall krabber funnet de 15 dagene i klassen [40,60> er helt jevnt fordelt. Det kan like gjerne være at de fant 59 krabber i 15 dager. Dette vet vi ikke, men kanskje Sebastian har en formening om det? Han kan altså ha rett, men vi vet det ikke sikkert.
d)
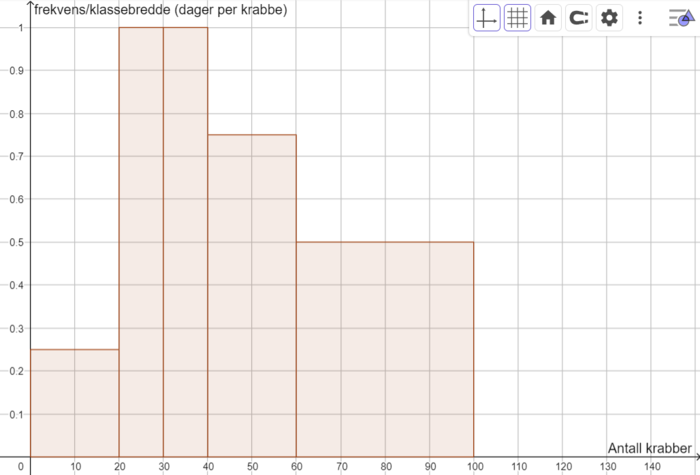
| Antall krabber | Klassebredde (b) | Antall dager (f) | Histogramhøyde (f/b) |
|---|---|---|---|
| [0,20> | 20 | 5 | 0,25 |
| [20,30> | 10 | 10 | 1 |
| [30,40> | 10 | 10 | 1 |
| [40,60> | 20 | 15 | 0,75 |
| [60,100> | 40 | 20 | 0,5 |
Siden dette er del 1, må du tegne histogrammet for hånd.
Oppgave 6
a)
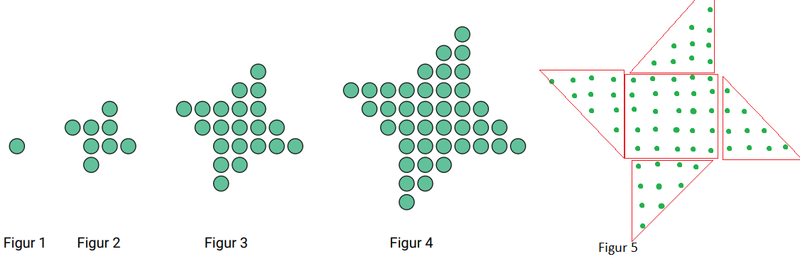
Jeg tegner figur 5 ved å følge mønsteret, og finner 65 prikker i figur nr. 5.
b)
| Figur nr. | 1 | 2 | 3 | 4 | 5 | n |
|---|---|---|---|---|---|---|
| Antall prikker | 1 | 8 | 21 | 40 | 65 | |
| Utregning |