1T 2024 vår LK20 LØSNING

Oppgaven som pdf

Diskusjon av oppgaven på matteprat

Løsning laget av Sindre Sogge Heggen

Del 1

Oppgave 1

a)

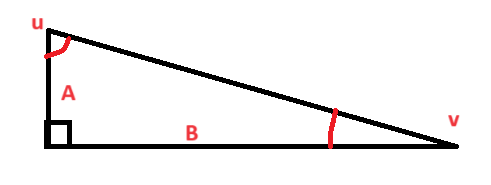
Tangens til vinkelen er definert som motstående katet, delt på hosliggende katet.

$\tan (u)\cdot \tan (v)=\frac{6}{8}\cdot \frac{8}{6}=1$

Dette betyr at Tom sin påstand er riktig.

b)

I denne oppgaven skal vi avgjøre om påstanden stemmer for alle rettvinklete trekanter.

Oppgave 2

Guri kan ha utført polynomdivisjon på to måter for å vise at faktoriseringen er riktig. Her er de to mulige polynomdivisjonene:

Divisjon av det opprinnelige polynomet med en av faktorene: Vi kan dele det opprinnelige polynomet

$2x^3+3x^2-11x-6$

med en av faktorene, for eksempel

$x-2$

Hvis vi får den andre faktoren som kvotient, bekrefter det at faktoriseringen er riktig.

Divisjon av det opprinnelige polynomet med kvotienten:

Vi kan også dele det opprinnelige polynomet

$2x^3+3x^2-11x-6$

med kvotienten

$2x^2+7x+3$

Hvis vi får

$x-2$

som resultat, bekrefter det også at faktoriseringen er riktig.