1T 2024 høst LØSNING

Oppgaven som pdf

Diskusjon av oppgaven på matteprat

DEL EN

Oppgave 1

$u={30}^{\circ }$

$2\cdot \sin (u)\cdot \cos (u)=2\cdot \frac{1}{2}\cdot \frac{\sqrt{3}}{2}=\frac{\sqrt{3}}{2}$

2u blir 60 grader og fra figuren ser vi at $\sin (2u)=\sin ({60}^{\circ })=\frac{\sqrt{3}}{2}$ så formelen stemmer.

Oppgave 2

Vi ser at dette er en andregradsfunksjon med nullpunkter for x= -3 og x = 1. Vi har symmetri så funksjonen vil ha sin laveste verdi når x = -1.

$f(-1)=(-1-1)(-1+3)=-2\cdot 2=-4$

Bunnpunkt (-1, 4)

Oppgave 3

Vi utfører en polynom divisjon for å faktorisere uttrykket.

Vi observerer at f(1) = 0, da er f delelig med (x-1).

$(x^3+7x^2+4x-12):(x-1)=x^2+8x+12$

$-(x^3-x^2)$

$8x^2+4x-12$

$-(8x^2-8x)$

$12x-12$

$-(12x-12)$

$0$

Så faktoriserer vi andregradsuttrykket:

Bruker ABC formelen og finner at $x_1=-6\vee x_2=-2$

Da har vi at $x^3+7x^2+4x-12=(x-1)(x+2)(x+6)$

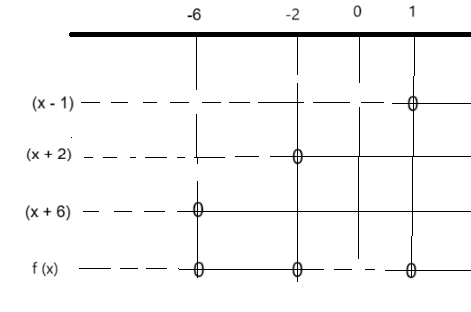
Så lager vi et fortegnsskjema for å finne ut for hvile verdier f(x) er negativ, null og positiv:

Da har vi et fortegnsskjema som viser når f er positiv og negativ. Dette stemmer med grafen nedenfor.

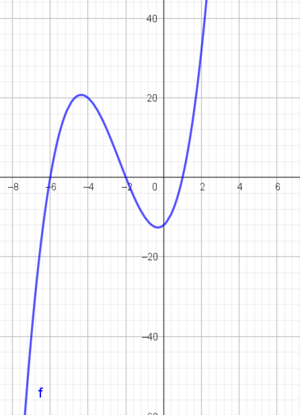
Da gjennstår det bare å se på $f(x)<0:$

f skal være mindre enn null. Det er den i området fra minus uendelig til -6 og mellom -2 og 1.

$x\in <\leftarrow ,-6>\cup <-2,1>$

Oppgave 4

a)

Tangens er sinus delt på cosinus. Tangens til 50 grader er større enn en fordi $\frac{0,77}{0,64}$ er større enn 1.

b)

Vinkelen befinner seg i andre kvadrant der cosinus er negativ og sinus positiv. Da er tangens negativ, altså mindre enn null.

Oppgave 5

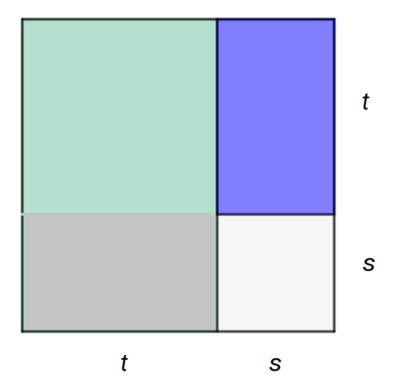
Arealet av det store kvadratet:

$(t+s)(t+s)=t^2+2ts+s^2$

Dette er en matematisk identitet, 1. kvadratsetning. Det andre leddet på høyre side, 2ts er arealet av de to rektangelene i fuguren, som begge har areal t ganger s.