Integrasjon II: Forskjell mellom sideversjoner
| Linje 66: | Linje 66: | ||
== Beregning av volumet av bauen == | == Beregning av volumet av bauen == | ||
Vi skal beregne volumet av bauen til | Vi skal beregne volumet av bauen for de første 6 fotene av båtens lengde. Båten har sin lengderetning langs **y-aksen**, slik at baugen ligger i origo \( (x,y) = (0,0) \) og strekker seg fra \( y = 0 \) til \( y = 6 \). | ||
: | Båtens bredde er gitt av parabelen: | ||
: | |||
\[ | |||
x_{\max} = 1.5y^2, \quad x_{\min} = -1.5y^2 | |||
\] | |||
Dybden under vannet er beskrevet av funksjonen: | |||
: | : | ||
\[ | \[ | ||
z = 0.5x^2 - 0.5y | |||
\] | \] | ||
Vi skal finne volumet under xy-planet, altså der \( z < 0 \). | |||
=== Volumintegral === | === Volumintegral === | ||
| Linje 83: | Linje 90: | ||
: | : | ||
\[ | \[ | ||
V = \int_0^6 \int_{-1. | V = \int_0^6 \int_{-1.5y^2}^{1.5y^2} (0.5x^2 - 0.5y) \, dx \, dy | ||
\] | \] | ||
### Indre integral (integrerer over x) | |||
Vi løser det indre integralet: | Vi løser det indre integralet: | ||
: | : | ||
\[ | \[ | ||
\int_{-1. | \int_{-1.5y^2}^{1.5y^2} (0.5x^2 - 0.5y) \, dx | ||
\] | \] | ||
| Linje 99: | Linje 105: | ||
: | : | ||
\[ | \[ | ||
\left[ 0. | \left[ 0.5 \frac{x^3}{3} - 0.5yx \right]_{-1.5y^2}^{1.5y^2} | ||
\] | \] | ||
| Linje 106: | Linje 112: | ||
: | : | ||
\[ | \[ | ||
= \left( 0. | = \left( 0.5 \cdot \frac{(1.5y^2)^3}{3} - 0.5y(1.5y^2) \right) - \left( 0.5 \cdot \frac{(-1.5y^2)^3}{3} - 0.5y(-1.5y^2) \right) | ||
\] | |||
: | |||
\[ | |||
= \left( 0.5 \cdot \frac{3.375y^6}{3} - 0.75y^3 \right) - \left( 0.5 \cdot \frac{-3.375y^6}{3} + 0.75y^3 \right) | |||
\] | \] | ||
: | : | ||
\[ | \[ | ||
= \left( 0. | = \left( 0.5 \cdot 1.125y^6 - 0.75y^3 \right) - \left( -0.5 \cdot 1.125y^6 + 0.75y^3 \right) | ||
\] | \] | ||
: | : | ||
\[ | \[ | ||
= (0. | = (0.5625y^6 - 0.75y^3) - (-0.5625y^6 + 0.75y^3) | ||
\] | \] | ||
: | : | ||
\[ | \[ | ||
= 1. | = 1.125y^6 - 1.5y^3 | ||
\] | \] | ||
### Ytre integral (integrerer over y) | |||
Nå integrerer vi dette over \( y \): | |||
: | |||
\[ | |||
V = \int_0^6 (1.125y^6 - 1.5y^3) \, dy | |||
\] | |||
: | : | ||
\[ | \[ | ||
= \left[ 1.125 \cdot \frac{y^7}{7} - 1.5 \cdot \frac{y^4}{4} \right]_0^6 | |||
\] | \] | ||
: | : | ||
\[ | \[ | ||
= \left[ 1. | = \left[ \frac{1.125}{7} \cdot 6^7 - \frac{1.5}{4} \cdot 6^4 \right] | ||
\] | \] | ||
: | : | ||
\[ | \[ | ||
= \left[ \frac{1.5}{ | = \left[ \frac{1.125}{7} \cdot 279936 - \frac{1.5}{4} \cdot 1296 \right] | ||
\] | \] | ||
: | : | ||
\[ | \[ | ||
= \frac{ | = \left[ \frac{315930}{7} - \frac{1944}{4} \right] | ||
\] | \] | ||
: | : | ||
\[ | \[ | ||
= \ | = \left[ 45132.86 - 486 \right] | ||
\] | \] | ||
: | |||
\[ | |||
= 44646.86 | |||
\] | |||
### Svar | |||
Volumet av bauen for de første 6 fotene av båtens lengde, under vannlinjen, er **44,647 kubikkfot** (avrundet). | |||
== Svar == | == Svar == | ||
Sideversjonen fra 1. mar. 2025 kl. 10:43
Det du leser her ligger utenfor pensum på vgs, men for interesserte elever kan det kanskje pirre nysgjerrigheten? Artikkelen er ikke ment å være en komplett lærebok, men en liten "teaser".
Dobbelintegrasjon: Grunnleggende prinsipper og anvendelser
Dobbelintegrasjon brukes for å beregne volum under en overflate, finne masse av tynne plater med variabel tetthet, og løse visse typer differensiallikninger.
Et dobbelintegral er av formen:
\[ \int_a^b \int_c^d f(x, y) \, dy \, dx \]
Her integrerer vi først over $y $ -variabelen og deretter over $ x $-variabelen. Vi integrerer alltid først det innerste integralet, så jobber vi oss utover (kan jo ha mer enn to integraler i hverandre).
Eksempel 1: Beregning av volum (av en kube)
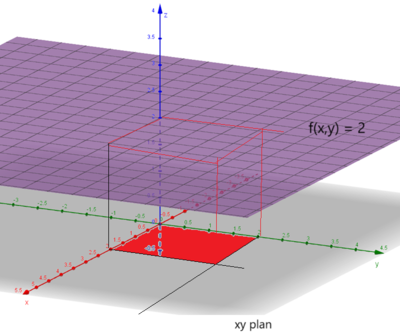
Vi ønsker å finne volumet av et område begrenset av xy- planet: <math> 0 \leq x \leq 2 </math> og <math> 0 \leq y \leq 2 </math> (Rødt område), og planet som er parallelt med xy planet og skjærer z- aksen i 2: <math> f(x, y) = 2 </math>.
<math> V = \int \int_A f(x,y) \, dy \, dx = \int_0^2 \int_0^2 2 \, dy \, dx = \int_0^2 [2y ]_0^2 \, dx = \int_0^2 4 \, dx = [4x ]_0^2 = 8 </math>
Dette var jo som forventet. Vi integrerte over det røde området som er et 2x2 kvadrat (ikke la deg lure av perspektivet), multiplisert med høyden som er 2 gir jo det et volum på 8 enheter.
Eksempel 2: Beregning av volum under en overflate
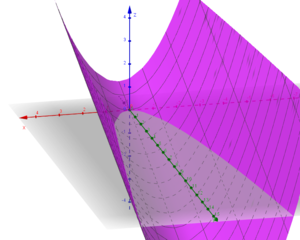
Baugen på en seilbåt kan beskrives av funksjonen $f(x,y) = \frac 12 x^2 - \frac 13 y $
Vi tenker at xy planet er havoverflaten og vi ønsker å beregne volumet av bauen, de 6 første fotene av båtens lengde.(Mindre båter oppgir oftest lengden i fot, ft.). Det volumet vi er på jakt etter ligger under xy planet og er avgrenset av $f(x,y) = \frac 12 x^2 - \frac 13 y $.
Hva så med integrasjonsgrensene?
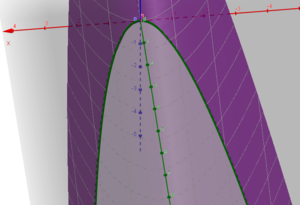
Beregning av volumet av bauen
Vi skal beregne volumet av bauen for de første 6 fotene av båtens lengde. Båten har sin lengderetning langs **y-aksen**, slik at baugen ligger i origo \( (x,y) = (0,0) \) og strekker seg fra \( y = 0 \) til \( y = 6 \).
Båtens bredde er gitt av parabelen:
\[ x_{\max} = 1.5y^2, \quad x_{\min} = -1.5y^2 \]
Dybden under vannet er beskrevet av funksjonen:
\[ z = 0.5x^2 - 0.5y \]
Vi skal finne volumet under xy-planet, altså der \( z < 0 \).
Volumintegral
Volumet beregnes som et dobbeltintegral:
\[ V = \int_0^6 \int_{-1.5y^2}^{1.5y^2} (0.5x^2 - 0.5y) \, dx \, dy \]
- Indre integral (integrerer over x)
Vi løser det indre integralet:
\[ \int_{-1.5y^2}^{1.5y^2} (0.5x^2 - 0.5y) \, dx \]
Beregning:
\[ \left[ 0.5 \frac{x^3}{3} - 0.5yx \right]_{-1.5y^2}^{1.5y^2} \]
Setter inn grensene:
\[ = \left( 0.5 \cdot \frac{(1.5y^2)^3}{3} - 0.5y(1.5y^2) \right) - \left( 0.5 \cdot \frac{(-1.5y^2)^3}{3} - 0.5y(-1.5y^2) \right) \]
\[ = \left( 0.5 \cdot \frac{3.375y^6}{3} - 0.75y^3 \right) - \left( 0.5 \cdot \frac{-3.375y^6}{3} + 0.75y^3 \right) \]
\[ = \left( 0.5 \cdot 1.125y^6 - 0.75y^3 \right) - \left( -0.5 \cdot 1.125y^6 + 0.75y^3 \right) \]
\[ = (0.5625y^6 - 0.75y^3) - (-0.5625y^6 + 0.75y^3) \]
\[ = 1.125y^6 - 1.5y^3 \]
- Ytre integral (integrerer over y)
Nå integrerer vi dette over \( y \):
\[ V = \int_0^6 (1.125y^6 - 1.5y^3) \, dy \]
\[ = \left[ 1.125 \cdot \frac{y^7}{7} - 1.5 \cdot \frac{y^4}{4} \right]_0^6 \]
\[ = \left[ \frac{1.125}{7} \cdot 6^7 - \frac{1.5}{4} \cdot 6^4 \right] \]
\[ = \left[ \frac{1.125}{7} \cdot 279936 - \frac{1.5}{4} \cdot 1296 \right] \]
\[ = \left[ \frac{315930}{7} - \frac{1944}{4} \right] \]
\[ = \left[ 45132.86 - 486 \right] \]
\[ = 44646.86 \]
- Svar
Volumet av bauen for de første 6 fotene av båtens lengde, under vannlinjen, er **44,647 kubikkfot** (avrundet).
Svar
Det totale volumet av bauen for de første 6 fotene av båtens lengde, med \( y \) avgrenset av parabelen \( y = \pm 1.5x^2 \), er **582 kubikkfot**.
Eksempel 3: Masseberegning med variabel tetthet
Vi har en plate definert på området <math> 0 \leq x \leq 1 </math> og <math> 0 \leq y \leq 1 </math>, med tetthet gitt ved $
h_o(x, y) = x^2 + y^2 $. Massens uttrykk blir:
\[ M = \int_0^1 \int_0^1 (x^2 + y^2) \, dy \, dx \]
Først integrerer vi med hensyn til <math> y </math>:
\[ \int_0^1 (x^2 + y^2) \, dy = x^2y + \frac{y^3}{3} \Big|_0^1 = x^2 + \frac{1}{3} \]
Så integrerer vi med hensyn til <math> x </math>:
\[ \int_0^1 (x^2 + \frac{1}{3}) \, dx = \frac{x^3}{3} + \frac{x}{3} \Big|_0^1 = \frac{1}{3} + \frac{1}{3} = \frac{2}{3} \]
Så massen er $ \frac{2}{3} $ masse-enheter.
Trippelintegrasjon
En trippelintegral brukes til å beregne volum i rommet eller masse i et tredimensjonalt objekt. Generelt har vi:
\[ \int_a^b \int_c^d \int_e^f f(x, y, z) \, dz \, dy \, dx \]
Her integrerer vi først over $z $, deretter $ y $, og til slutt $ x $.
Eksempel 4: Beregning av volum i en kube
Vi ønsker å finne volumet av en kube med sidelengde 1, altså området <math> 0 \leq x \leq 1 </math>, <math> 0 \leq y \leq 1 </math>, <math> 0 \leq z \leq 1 </math>. Vi setter <math> f(x, y, z) = 1 </math>.
<math> V = \int_0^1 \int_0^1 \int_0^1 1 \, dz \, dy \, dx </math>
Integrerer først med hensyn til <math> z </math>:
<math> \int_0^1 1 \, dz = z \Big|_0^1 = 1 </math>
Deretter med hensyn til <math> y </math>:
<math> \int_0^1 1 \, dy = y \Big|_0^1 = 1 </math>
Til slutt med hensyn til <math> x </math>:
<math> \int_0^1 1 \, dx = x \Big|_0^1 = 1 </math>
Så volumet er <math> 1 </math> kubikkenhet.
Dobbelintegrasjon er et kraftig verktøy for å finne arealer, volum og masse i fysikk og matematikk. Den lar oss analysere hvordan en funksjon oppfører seg over et todimensjonalt område.
Forskjellen mellom dobbel og trippel integrasjon for volum
Både dobbel integrasjon og trippel integrasjon kan brukes til å beregne volum, men de anvendes i ulike situasjoner avhengig av hvordan volumet er beskrevet.
- Dobbel integrasjon
Brukes når volumet kan beskrives som området under en funksjon \( z = f(x,y) \) over et gitt område i planet.
- Trippel integrasjon
Brukes når volumet må beskrives i hele rommet, dvs. når man jobber med en funksjon \( f(x,y,z) \) innenfor et tredimensjonalt område.
Dobbel integrasjon brukes altså når høyden \( z \) kan uttrykkes eksplisitt som en funksjon av \( x \) og \( y \), mens trippel integrasjon er nødvendig når volumet har en mer kompleks struktur i tre dimensjoner.
Eksempler på dobbel integrasjon
Eksempel 1: Volumet under en paraboloide
Finn volumet av området under paraboloiden \( z = 4 - x^2 - y^2 \) over sirkelskiven \( x^2 + y^2 \leq 4 \).
Løsning: Vi bruker polarkoordinater: \[ V = \iint_D (4 - x^2 - y^2) \, dA \] I polarkoordinater (\( x = r\cos\theta \), \( y = r\sin\theta \)): \[ V = \int_0^{2\pi} \int_0^2 (4 - r^2) r \, dr \, d\theta \]
Eksempel 2: Volum mellom to flater
Finn volumet mellom flatene \( z = x^2 + y^2 \) og \( z = 2 - x^2 - y^2 \) over området \( x^2 + y^2 \leq 1 \).
Løsning: Volumet er gitt ved integralet: \[ V = \iint_D [(2 - x^2 - y^2) - (x^2 + y^2)] \, dA \] I polarkoordinater: \[ V = \int_0^{2\pi} \int_0^1 (2 - 2r^2) r \, dr \, d\theta \]
Trippel integrasjon
Eksempel 3: Volum av en kule
Finn volumet av en kule med radius \( R \), gitt ved \( x^2 + y^2 + z^2 \leq R^2 \).
Løsning: Bruk kulekoordinater (\( x = r\sin\theta\cos\phi \), \( y = r\sin\theta\sin\phi \), \( z = r\cos\theta \)): \[ V = \int_0^{2\pi} \int_0^{\pi} \int_0^R r^2 \sin\theta \, dr \, d\theta \, d\phi \]
Eksempel 4: Volum av et tetraeder
Finn volumet av tetraederet med hjørner i \( (0,0,0) \), \( (a,0,0) \), \( (0,b,0) \) og \( (0,0,c) \).
Løsning: Integrasjonsgrenser bestemmes av planlikningen \( \frac{x}{a} + \frac{y}{b} + \frac{z}{c} = 1 \), så volumet er: \[ V = \int_0^a \int_0^{b(1 - x/a)} \int_0^{c(1 - x/a - y/b)} dz \, dy \, dx \]