Integrasjon II

Det du leser her ligger utenfor pensum på vgs, men for interesserte elever kan det kanskje pirre nysgjerrigheten? Artikkelen er ikke ment å være en komplett lærebok, men en liten "teaser".

Forskjellen mellom dobbel og trippel integrasjon for volum

Både dobbel integrasjon og trippel integrasjon kan brukes til å beregne volum, men de anvendes i ulike situasjoner avhengig av hvordan volumet er beskrevet.

• Dobbel integrasjon

Brukes når volumet kan beskrives som området under en funksjon \( z = f(x,y) \) over et gitt område i planet. Man må integrere over deler av ett av de tre akseplanene, xy, yz eller xz, samt plan som er paralelle med disse.

• Trippel integrasjon

Brukes når volumet må beskrives i hele rommet, dvs. når man jobber med en funksjon \( f(x,y,z) \) innenfor et tredimensjonalt område.

Dobbel integrasjon brukes altså når høyden \( z \) kan uttrykkes eksplisitt som en funksjon av \( x \) og \( y \), mens trippel integrasjon er nødvendig når volumet har en mer kompleks struktur i tre dimensjoner.

Dobbelintegrasjon: Grunnleggende prinsipper og anvendelser

Dobbelintegrasjon brukes for å beregne volum under en overflate, finne masse av tynne plater med variabel tetthet, og løse visse typer differensiallikninger.

Et dobbelintegral er av formen:

\[ \int_a^b \int_c^d f(x, y) \, dy \, dx \]

Her integrerer vi først over $y $ -variabelen og deretter over $ x $-variabelen. Vi integrerer alltid først det innerste integralet, så jobber vi oss utover (kan jo ha mer enn to integraler i hverandre).

Man integrerer over et plan:

\[ dA = dxdy = dydx \]

Eksempel 1: Beregning av volum (av en kube)

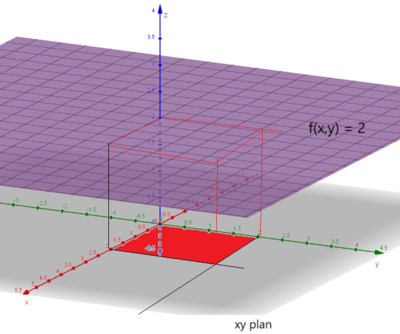
Vi ønsker å finne volumet av et område begrenset av xy- planet: <math> 0 \leq x \leq 2 </math> og <math> 0 \leq y \leq 2 </math> (Rødt område), og planet som er parallelt med xy planet og skjærer z- aksen i 2: <math> f(x, y) = 2 </math>.

<math> V = \int \int_A f(x,y) \, dy \, dx = \int_0^2 \int_0^2 2 \, dy \, dx = \int_0^2 [2y ]_0^2 \, dx = \int_0^2 4 \, dx = [4x ]_0^2 = 8 </math>

Dette var jo som forventet. Vi integrerte over det røde området som er et 2x2 kvadrat (ikke la deg lure av perspektivet), multiplisert med høyden som er 2 gir jo det et volum på 8 enheter.

Eksempel 2: Beregning av volum under en overflate

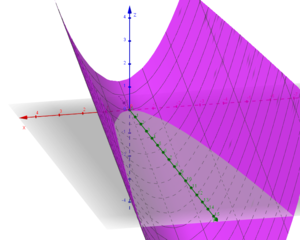
Baugen på en seilbåt kan beskrives av funksjonen $f(x,y) = \frac 12 x^2 - \frac 13 y $

Vi tenker at xy planet er havoverflaten og vi ønsker å beregne volumet av bauen, de 6 første fotene av båtens lengde.(Mindre båter oppgir oftest lengden i fot, ft.). Det volumet vi er på jakt etter ligger under xy planet og er avgrenset av $f(x,y) = \frac 12 x^2 - \frac 13 y $.

Hva så med integrasjonsgrensene?

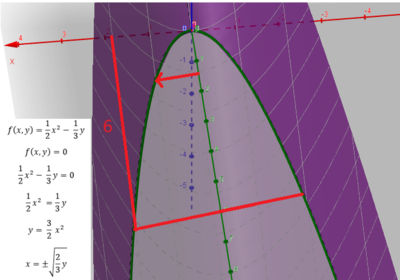
Vi har symmetri rund y aksen og integrerer fra 0 til f, og multipliserer med 2.

\[ V = 2 \int_0^6 \int_0^{(\frac 23y)^{\frac 12}} (\frac 12 x^2 + \frac 13 y) \, dx \, dy \]

\[ V = 2 \int_0^6 [\frac 16 x^3 + \frac 13 yx]_0^{(\frac 23y)^{\frac 12}} \, dy \]

\[ V = 2 \int_0^6 (\frac 16( \frac 23)^{\frac 32} y^{\frac 32} - \frac 13( \frac 23)^{\frac 12} y^{\frac 32}) \, dy \]

\[ V = 2 \int_0^6 ((\frac 16( \frac 23)^{\frac 32} - \frac 13( \frac 23)^{\frac 12}) y^{\frac 32}) \, dy \]

\[ V = 2 [(\frac 16( \frac 23)^{\frac 32} - \frac 13( \frac 23)^{\frac 12}) \cdot \frac 25 \cdot y^{\frac 52})]_0^6 \]

\[ V = 2 (\frac 16( \frac 23)^{\frac 32} - \frac 13( \frac 23)^{\frac 12}) \cdot \frac 25 \cdot 6^{\frac 52}) \approx -12,8 \]

Man kan løse doble integraler i Geogebra, ved å løse de to integralene hver for seg

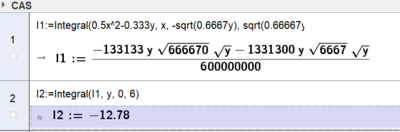
Svaret vi får er negativt fordi volumet vårt ligger under xy planet. Vi tar absoluttverdien og får ca 12, 8 kubikkfot.

Integrasjonsrekkefølge

Å endre integrasjonsrekkefølgen i et dobbeltintegral kan være nyttig av flere grunner:

Forenkling av beregninger: Noen ganger er det lettere å evaluere integralet ved å bytte rekkefølge. For eksempel kan den indre integrasjonen bli enklere, eller det kan gjøre det mulig å bruke en kjent antiderivert.

Unngå vanskelige grenser: Når integrasjonsrekkefølgen endres, kan grensene for integralet ofte omskrives til en enklere form. Dette er spesielt nyttig hvis de opprinnelige grensene er kompliserte eller involverer vanskelige funksjoner.

Gjøre integralet løsbart: Noen ganger kan et dobbeltintegral være umulig eller svært vanskelig å løse i én rekkefølge, men mulig i en annen. Dette skjer ofte hvis integralet inneholder en funksjon som er vanskelig å integrere i én retning, men enkel i en annen.

Numerisk evaluering: I numeriske metoder kan det være mer effektivt å endre integrasjonsrekkefølgen for å redusere beregningskompleksiteten.

Teoretiske grunner: Noen ganger endres rekkefølgen for å illustrere en matematisk egenskap, for eksempel ved bruk av Fubinis teorem eller for å bevise likhet mellom forskjellige integraluttrykk.

Kort sagt, endring av integrasjonsrekkefølgen er et kraftig verktøy for å gjøre integraler enklere å håndtere, enten analytisk eller numerisk.

Eksempel på endring av integreringsrekkefølge for å forenkle beregninger

Vi vurderer det dobbeltintegralet:

<math> I = \int_0^1 \int_y^1 e^{x^2} \, dx \, dy. </math>

1. Opprinnelig rekkefølge

Grensene sier at for en fast <math>y</math>, varierer <math>x</math> fra <math>y</math> til <math>1</math>. Problemet er at den indre integrasjonen

<math> \int_y^1 e^{x^2} \, dx </math>

har ingen elementær antiderivert, noe som gjør den vanskelig å løse direkte.

2. Endring av rekkefølge

Vi bytter integrasjonsrekkefølge ved å beskrive området på en annen måte:

• <math>x</math> går fra <math>0</math> til <math>1</math>.
• For en gitt <math>x</math>, varierer <math>y</math> fra <math>0</math> til <math>x</math>, fordi <math>y \leq x</math> i det opprinnelige integralet.

Dermed omskriver vi integralet som:

<math> I = \int_0^1 \int_0^x e^{x^2} \, dy \, dx. </math>

Den indre integrasjonen er nå enkel:

<math> \int_0^x e^{x^2} \, dy = e^{x^2} \cdot (x - 0) = x e^{x^2}. </math>

Dermed reduseres integralet til:

<math> I = \int_0^1 x e^{x^2} \, dx. </math>

3. Løsning

Vi bruker substitusjon: Sett <math>u = x^2</math>, da er <math>du = 2x dx</math>, eller <math>\frac{du}{2} = x dx</math>.

Grensene endres fra <math>x = 0</math> til <math>x = 1</math>, som gir <math>u = 0</math> til <math>u = 1</math>, så vi får:

<math> I = \int_0^1 e^u \frac{du}{2} = \frac{1}{2} \int_0^1 e^u \, du. </math>

Dette løses enkelt:

<math> I = \frac{1}{2} \left[ e^u \right]_0^1 = \frac{1}{2} (e^1 - e^0) = \frac{1}{2} (e - 1). </math>

4. Konklusjon

Ved å bytte rekkefølge på integralet gikk vi fra et uløselig integral til et som enkelt kunne beregnes ved substitusjon. Dette viser hvorfor det kan være nyttig å endre integrasjonsrekkefølgen.

Trippelintegrasjon

En trippelintegral brukes til å beregne volum i rommet eller masse i et tredimensjonalt objekt. Generelt har vi:

\[ \int_a^b \int_c^d \int_e^f f(x, y, z) \, dz \, dy \, dx \]

Her integrerer vi først over $z $, deretter $ y $, og til slutt $ x $.

Eksempel 4: Beregning av volum i en kube

Vi ønsker å finne volumet av en kube med sidelengde 1, altså området <math> 0 \leq x \leq 1 </math>, <math> 0 \leq y \leq 1 </math>, <math> 0 \leq z \leq 1 </math>. Vi setter <math> f(x, y, z) = 1 </math>.

<math> V = \int_0^1 \int_0^1 \int_0^1 1 \, dz \, dy \, dx </math>

Integrerer først med hensyn til <math> z </math>:

<math> \int_0^1 1 \, dz = z \Big|_0^1 = 1 </math>

Deretter med hensyn til <math> y </math>:

<math> \int_0^1 1 \, dy = y \Big|_0^1 = 1 </math>

Til slutt med hensyn til <math> x </math>:

<math> \int_0^1 1 \, dx = x \Big|_0^1 = 1 </math>

Så volumet er <math> 1 </math> kubikkenhet.

Dobbelintegrasjon er et kraftig verktøy for å finne arealer, volum og masse i fysikk og matematikk. Den lar oss analysere hvordan en funksjon oppfører seg over et todimensjonalt område.

Eksempler på dobbel integrasjon

Eksempel 1: Volumet under en paraboloide

Finn volumet av området under paraboloiden \( z = 4 - x^2 - y^2 \) over sirkelskiven \( x^2 + y^2 \leq 4 \).

Løsning: Vi bruker polarkoordinater: \[ V = \iint_D (4 - x^2 - y^2) \, dA \] I polarkoordinater (\( x = r\cos\theta \), \( y = r\sin\theta \)): \[ V = \int_0^{2\pi} \int_0^2 (4 - r^2) r \, dr \, d\theta \]

Eksempel 2: Volum mellom to flater

Finn volumet mellom flatene \( z = x^2 + y^2 \) og \( z = 2 - x^2 - y^2 \) over området \( x^2 + y^2 \leq 1 \).

Løsning: Volumet er gitt ved integralet: \[ V = \iint_D [(2 - x^2 - y^2) - (x^2 + y^2)] \, dA \] I polarkoordinater: \[ V = \int_0^{2\pi} \int_0^1 (2 - 2r^2) r \, dr \, d\theta \]

Trippel integrasjon

Eksempel 3: Volum av en kule

Finn volumet av en kule med radius \( R \), gitt ved \( x^2 + y^2 + z^2 \leq R^2 \).

Løsning: Bruk kulekoordinater (\( x = r\sin\theta\cos\phi \), \( y = r\sin\theta\sin\phi \), \( z = r\cos\theta \)): \[ V = \int_0^{2\pi} \int_0^{\pi} \int_0^R r^2 \sin\theta \, dr \, d\theta \, d\phi \]

Eksempel 4: Volum av et tetraeder

Finn volumet av tetraederet med hjørner i \( (0,0,0) \), \( (a,0,0) \), \( (0,b,0) \) og \( (0,0,c) \).

Løsning: Integrasjonsgrenser bestemmes av planlikningen \( \frac{x}{a} + \frac{y}{b} + \frac{z}{c} = 1 \), så volumet er: \[ V = \int_0^a \int_0^{b(1 - x/a)} \int_0^{c(1 - x/a - y/b)} dz \, dy \, dx \]