Trekant: Forskjell mellom sideversjoner
Fra Matematikk.net
Ingen redigeringsforklaring |
m Teksterstatting – «<tex>» til «<math>» |
||
| Linje 1: | Linje 1: | ||
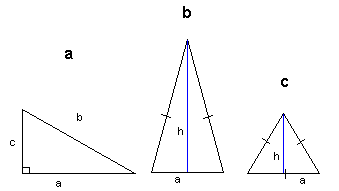
Vi har forskjellige typer trekanter, a er rettvinklet, b er likebeint og c er likesidet. Enkelte trekanter er både rettvinklet og likebeinte. Figur b og c er også spissvinklede trekanter. I en likebeint trekant er to sider like lange og to vinkler like store. I en likesidet trekant er alle sidene like lange og alle vinklene 60° | Vi har forskjellige typer trekanter, a er rettvinklet, b er likebeint og c er likesidet. Enkelte trekanter er både rettvinklet og likebeinte. Figur b og c er også spissvinklede trekanter. I en likebeint trekant er to sider like lange og to vinkler like store. I en likesidet trekant er alle sidene like lange og alle vinklene 60° | ||
Summen av alle vinklene i en trekant er alltid 180°. Arealet av en trekant er grunnlinjen multiplisert med høyden, dividert på to, eller, < | Summen av alle vinklene i en trekant er alltid 180°. Arealet av en trekant er grunnlinjen multiplisert med høyden, dividert på to, eller, <math> A = \frac{Gh}{2}</tex>. På figuren nedenfor er G = a. | ||
[[Bilde:Trekanter.gif]] | [[Bilde:Trekanter.gif]] | ||
Sideversjonen fra 5. feb. 2013 kl. 20:58
Vi har forskjellige typer trekanter, a er rettvinklet, b er likebeint og c er likesidet. Enkelte trekanter er både rettvinklet og likebeinte. Figur b og c er også spissvinklede trekanter. I en likebeint trekant er to sider like lange og to vinkler like store. I en likesidet trekant er alle sidene like lange og alle vinklene 60°
Summen av alle vinklene i en trekant er alltid 180°. Arealet av en trekant er grunnlinjen multiplisert med høyden, dividert på to, eller, <math> A = \frac{Gh}{2}</tex>. På figuren nedenfor er G = a.
I en rettvinklet trekant har de to sidene som danner den rette vinkelen (a og c) navnet kateter. Den lengste siden motstående til den rette vinkelen har navnet hypotenus (b).