R2 2009 høst LØSNING

Del 1

Oppgave 1

a)

$f(x)=x^2\sin (x)\Rightarrow f^{\prime }(x)=(x^2{)}^{\prime }\sin (x)+x^2(\sin (x){)}^{\prime }=2x\sin (x)+x^2\cos (x)$

b)

Radianer er en måte å måle vinkler på der en rett linje tilsvarer $\pi$ radianer. Sammenhengen mellom grader og radianer er gitt ved at $w=\frac{v}{180}\pi$ der $v$ er grader og $w$ radianer.

c)

Vi har multipliserer med integrerende faktor $e^{\int 2dx}=e^{2x}$ og får at $y^{\prime }{e}^{2x}+2y{e}^{2x}=3x{e}^{2x}$. Omskrivning av venstre side gir at $(y{e}^{2x}{)}^{\prime }=3x{e}^{2x}$. Integrasjon gir videre at $y{e}^{2x}=\int 3x{e}^{2x}dx=[\frac{3}{2}x{e}^{2x}]-\int \frac{3}{2}{e}^{2x}dx=\frac{3}{2}x{e}^{2x}-\frac{3}{4}{e}^{2x}+C$. Multiplikasjon med $e^{-2x}$ gir til slutt at $y=\frac{3}{2}x-\frac{3}{4}+C{e}^{-2x}$. Startbetingelsen $y(0)=3$ gir at $y(0)=3=-\frac{3}{4}+C$, så $C=3+\frac{3}{4}=\frac{15}{4}$, og $y(x)=\frac{3}{2}x-\frac{3}{4}+\frac{15}{4}{e}^{-2x}$

d)

La $f(x)=x^3-x^2-4x+4$

1) $f(1)=1^3-1^2-4+4=0$, så $(x-1)$ er en faktor i $f(x)$. Polynomdivisjon gir at $x^3-x^2-4x+4:x-1=x^2-4=(x+2)(x-2)$. Så $f(x)=(x-1)(x-2)(x+2)$

2) Delbrøksoppspaltning gir at $\frac{x^2-2x+4}{(x-1)(x-2)(x+2)}=\frac{A}{x-1}+\frac{B}{x-2}+\frac{C}{x+2}$. Multipliserer vi med $(x-1)(x-2)(x+2)$ får vi at $x^2-2x+4=A(x-2)(x+2)+B(x-1)(x+2)+C(x-1)(x-2)=(A+B+C)x^2+(B-3C)x-4A-2B+2C$. Sammenligning av koeffisientene gir at $A+B+C=1$, $B-3C=-2$ og $-2A-B+C=2$ med løsning $A=-1$, $B=C=1$. Altså er $\frac{x^2-2x+4}{(x-1)(x-2)(x+2)}=-\frac{1}{x-1}+\frac{1}{x-2}+\frac{1}{x+2}$.

3) $\int -\frac{1}{x-1}+\frac{1}{x-2}+\frac{1}{x+2}dx=-\ln (|x-1|)+\ln (|x-2|)+\ln (|x+2|)+C$

e)

Leddene i en geometrisk rekke er på formen $a{k}^n$. Forholdet mellom to påfølgende ledd er dermed $\frac{a{k}^{n+1}}{a{k}^n}=k$, så vi må ha at $k=\frac{2x}{x-1}=\frac{4x+8}{2x}$. Altså er $4x^2=(4x+8)(x-1)=4x^2-4x+8x-8$, så $4x=8$. Vi må derfor ha at $x=2$, og leddene blir $a_1=x-1=2-1=1$, $a_2=2x=2\cdot 2=4$ og $a_3=4x+8=4\cdot 2+8=16$. Altså er $a_n=4^{n-1}=\frac{1}{4}{4}^n$.

f)

Induksjonssteg 1: $s_1=\frac{a_1(k^1-1)}{k-1}=a_1$, så formelen er riktig for $n=1$.

Induksjonssteg 2: Anta at formelen er riktig for $n=m$. Da er $s_m=\frac{a_1(k^m-1)}{k-1}$, og $s_{m+1}=s_m+a_{m+1}=\frac{a_1(k^m-1)}{k-1}+a_1{k}^m=\frac{a_1(k^m-1+k^m(k-1))}{k-1}=\frac{a_1(k^{m+1}-1)}{k-1}$, så formelen er riktig for $n=m+1$. Det følger at formelen er riktig for alle naturlige tall.

Oppgave 2

a)

$\overrightarrow{AB}=[2,1,2]$ og $\overrightarrow{AC}=[1,6,4]$, så $\overrightarrow{AB}\cdot \overrightarrow{AC}=2+6+8=16$.

b)

$\overrightarrow{AB}\times \overrightarrow{AC}=[-8,-6,11]$

c)

La $P=(x,y,z)$ være et punkt i planet$\alpha$, slik at vektoren $\overrightarrow{AP}=[x-1,y-1,z-1]$ ligger i planet. $\overrightarrow{AB}\times \overrightarrow{AC}$ står vinkelrett på planet, så vi må ha at $(\overrightarrow{AB}\times \overrightarrow{AC})\cdot \overrightarrow{AP}=[-8,-6,11]\cdot [x-1,y-1,z-1]=-8x+8-6y+6+11z-11=0$. Ligningen for $\alpha$ blir derfor $8x+6y-11z=3$. Punktet $(x,y,z)=(2,2,3)$ tilfredsstiller ikke ligningen, og ligger derfor ikke i planet.

d)

En parameterfremstilling for en linje gjennom $D$, parallell med $\overrightarrow{AB}\times \overrightarrow{AC}$ er $\overrightarrow{r}(t)=[2,2,3]+t[-8,-6,11]=[2-8t,2-6t,3+11t]$. $S$ er dermed bestemt ved at $[8,6,-11]\cdot [2-8t,2-6t,3+11t]=16-64t+12-36t-33-121t=-221t-5=3$, så $t=-\frac{8}{221}$.

Del 2

Oppgave 3

a)

Arealet av trekanten kan skrives på to måter:

$\frac{a\cdot b}{2}=\frac{c\cdot h}{2}$ dvs

$a\cdot b=c\cdot h$

Pytagoras gir

$a^2+b^2=c^2$ der $c=\frac{ab}{h}$ (fra injene over)

Det gir:

$a^2+b^2=(\frac{ab}{h}{)}^2$

$a^2+b^2=\frac{a^2{b}^2}{h^2}$

$\frac{a^2}{a^2{b}^2}+\frac{b^2}{a^2{b}^2}=\frac{1}{h^2}$

$\frac{1}{b^2}+\frac{1}{a^2}=\frac{1}{h^2}$ Hvilket skulle vises.

b)

$\overrightarrow{AB}\times \overrightarrow{AC}=[bc,ac,ab]$

Arealet av trekanten blir da

$\frac{1}{2}\sqrt{b^2{c}^2+a^2{c}^2+a^2{b}^2}$

c)

$F_{\mathrm{△}ABC}^2=F_{\mathrm{△}OAC}^2+F_{\mathrm{△}OBC}^2+F_{\mathrm{△}OAB}^2$

Fra b har man at

$F_{\mathrm{△}ABC}^2=\frac{1}{4}(b^2{c}^2+a^2{C}^2+a^2{b}^2)$

Man finner så arealet av de tre andre trekantene ved å bruke vektorproduktet, og får:

$F_{\mathrm{△}OAC}^2=\frac{1}{4}(a^2{C}^2)$

$F_{\mathrm{△}OBC}^2=\frac{1}{4}(b^2{c}^2)$

$F_{\mathrm{△}ABC}^2=\frac{1}{4}(a^2{b}^2)$

Man ser da et arealsetningen er riktig.

d)

Volumet av figuren OABC kan skrives:

$\frac{1}{2}\cdot a\cdot b\cdot c\cdot \frac{1}{3}=F_{\mathrm{△}ABC}\cdot h\cdot \frac{1}{3}$

som gir:

$F_{\mathrm{△}ABC}=\frac{a\cdot b\cdot c}{2h}$

e)

Man har:

$F_{\mathrm{△}ABC}^2=\frac{1}{4}(b^2{c}^2+a^2{C}^2+a^2{b}^2)$ og $F_{\mathrm{△}ABC}=\frac{a\cdot b\cdot c}{2h}$

Kombinert gir det

$(\frac{a\cdot b\cdot c}{2h}{)}^2=\frac{1}{4}(b^2{c}^2+a^2{C}^2+a^2{b}^2)$

$\frac{a^2\cdot b^2\cdot c^2}{4h^2}=\frac{1}{4}(b^2{c}^2+a^2{C}^2+a^2{b}^2)$

$\frac{1}{h^2}=\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}$

Oppgave 4

Alternativ I

a)

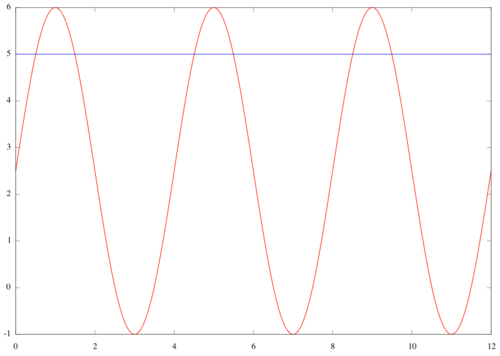
Avstanden langs x-aksen mellom påfølgende topp- og bunnpunkt er konstant, altså er det toppunkt i $x=5$. Funksjonen har toppunkt i $(1,6)$ og bunnpunkt i $(3,-1)$ og $(7,-1)$. La $f(x)=a\cos (cx-\phi )+d$. Vi kan anta at $a>0$ (Hvis $a<0$ kan vi skrive $a\cos (\theta )=-a\cos (\pi -\theta )$ ): I toppunktet er $\cos =1$ og i bunnpunktet $\cos =-1$, så vi må ha at $6=a+d$ og $-1=-a+d$. Det følger at $a=\frac{7}{2}$ og $d=\frac{5}{2}$. Vi må også ha at $\cos (c-\phi )=1$ og $\cos (3c-\phi )=-1$, så $c-\phi =0$ og $3c-\phi =\pi$, så $2c=\pi$ og $2\phi =\pi$. Vi får altså at $f(x)=\frac{7}{2}\cos (\frac{\pi }{2}x-\frac{\pi }{2})+\frac{5}{2}=\frac{7}{2}\sin (\frac{\pi }{2}x)+\frac{5}{2}$

b)

Løser vi ligningen <math>f(x)=0</math> blir $x=2n,n\in \{1,2,3,4,5\}$. $f^{\prime }(x)$ har bunnpunkt i $x=2$, $x=6$ og $x=10$, og der avtar $f(x)$ raskest.

c)

Vi løser $\frac{7}{2}\sin (\frac{\pi }{2}x)+\frac{5}{2}=0$, og får løsningene $x=\frac{2(2\pi n-\arcsin (\frac{5}{7}))}{\pi }$ og $x=\frac{2(2\pi n+\pi +\arcsin (\frac{5}{7}))}{\pi }$ for $n\in \mathbb{Z}$. I intervallet $⟨0,12⟩$ er nullpunktene tilnærmet $2.51$, $3.49$, $6.51$, $7.49$, $10.51$, og $11.49$

d)

Vi må først finne skjæringspunktene mellom $f(x)$(rød) og linja(blå) $y=5$. Altså må vi løse ligningen $f(x)=\frac{7}{2}\sin (\frac{\pi }{2}x)+\frac{5}{2}=5$. De to første løsningene er tilnærmet $x=0.51$ og $x=1.49$. Det samlede arealet av områdene avgrenset av kurvene, over $y=5$, blir dermed $3{\int }_{0.51}^{1.49}\frac{7}{2}\sin (\frac{\pi }{2}x)+\frac{5}{2}-5dx\approx 1.95$.

Alternativ II

a)

Volumet $V={\int }_0^9\pi f(x{)}^{2}dx=\pi {\int }_0^{9}xdx=\frac{\pi }{2}[x^2{]}_0^9=\frac{81\pi }{2}$

b)

Radius til omdreiningslegemet er $|f(x)-k|=|x^{\frac{1}{2}}-k|$. Volumet blir følgelig $V(k)={\int }_0^9\pi (x^{\frac{1}{2}}-k{)}^{2}dx$

c)

Vi har at $(x^{\frac{1}{2}}-k{)}^2=x-2k{x}^{\frac{1}{2}}+k^2$, så $V(k)={\int }_0^9\pi (x^{\frac{1}{2}}-k{)}^{2}dx=\pi {\int }_0^{9}x-2k{x}^{\frac{1}{2}}+k^{2}dx=\pi [\frac{1}{2}{x}^2-\frac{4k}{3}{x}^{\frac{3}{2}}+k^{2}x{]}_0^9=9\pi (\frac{9}{2}-4k+k^2)$

d)

Vi nullstiller den deriverte $V^{\prime }(k)=9\pi (2k-4)=0\Rightarrow k=2$. <math>V(k)</math> er positiv, så $V(k)$ har et bunnpunkt i $k=2$.

Oppgave 5

a)

Siden ballen slippes med null starthastighet er $v(0)=0$. Integrerende faktor er $e^{\int \frac{1}{4}dt}=e^{\frac{1}{4}t}$. Vi multipliserer ligningen med integrerende faktor, omskriver venstresida og får $(e^{\frac{1}{4}t}v{)}^{\prime }=10e^{\frac{1}{4}t}$. Integrasjon gir at $e^{\frac{1}{4}t}v=\int 10e^{\frac{1}{4}t}dt=40e^{\frac{1}{4}t}+C$, så $v(t)=40+C{e}^{-\frac{1}{4}t}$. Startbetingelsen gir at $C=-40$, så løsningen på startverdiproblemet blir $v(t)=40-40e^{-\frac{1}{4}t}$

b)

$s^{\prime }(t)=v(t)=40-40e^{-\frac{1}{4}t}$. Integrasjon gir at $s(t)=\int 40-40e^{-\frac{1}{4}t}dt=40t+160e^{-\frac{1}{4}t}+C$. Startbetingelsen $s(0)=0$ gir at $C=-160$, så løsningen blir $s(t)=40t+160e^{-\frac{1}{4}t}-160$

c)

Vi må løse ligningen $30=s(t)=40t+160e^{-\frac{1}{4}t}-160$ grafisk. Løsningen er $t\approx 2.73$. Farten er da $v(2.73)\approx 19.8\frac{\text{m}}{\text{s}}$.

d)

Hastigheten er gitt ved $v(t)=40+C{e}^{-\frac{1}{4}t}$. Med startbetingelsen $v(0)=v_0$, blir $C=v_0-40$, så $v(t)=40+(v_0-40)e^{-\frac{1}{4}t}$. Vi får videre at $s(t)=\int v(t)dt=\int 40+(v_0-40)e^{-\frac{1}{4}t}dt=40t-4(v_0-40)e^{-\frac{1}{4}t}+D$. Startbetingelsen $s(0)=0$ gir at $D=4v_0-160$, så $s(t)=40t-4(v_0-40)e^{-\frac{1}{4}t}+4v_0-160$. Vi må nå løse ligningen $s(2)=30$: $30=80-4(v_0-40)e^{-\frac{1}{2}}+4v_0-160\Rightarrow v_0\approx 8.23$. Starthastigheten må være omtrent $8.23\frac{\text{m}}{\text{s}}$ for at ballen skal bruke $2$ sekunder på å falle $30$ meter.