1P 2011 høst LØSNING

Løsning fra NDLA

DEL EN

Oppgave 1:

a)

$$\begin{gathered} \frac{x}{6}=\frac{5}{1,5} \\ 1,5x=30 \\ x=20 \end{gathered}$$

Det trengs 20 dl, eller 2 liter vann for å lage havregrøt av 6 dl gryn.

b)

Vi har ikke kalkulator, men bruker Pytagoras likevel. Summen av kvadratene utspendt av katetene er $6^2+5^2=36+25=61$. Dette skal være lik kvadratet utspendt av hypotenusen. Tenker vi på kvadrattallene vet vi at $7^2=49$ og $8^2=64$. Vi trenger altså mer enn syv lengder, altså må hun kjøpe 8 lengder.

c)

1)

$\frac{184}{160}=1,15$, dvs. 15% økning.

2)

Da har den også økt med 15%, altså fra 100 til 115.

d)

Hun har totalt 8 pakker å velge mellom.

1)

P(Kiwigele) = $\frac{2}{8}=25$%

Det er 25% sannsynlighet for at den første pakken hun trekker er kiwi.

2)

P(Kiwigele) = $\frac{2}{8}\cdot \frac{1}{7}=\frac{2}{56}=3,6$%

Det er 3,6% sjangse for at begge pakkene hun trekker er kiwigele.

3)

Sannsynlighet for en pakke blåbær og en pakke kiwi gele:

P(en kiwigele og en blåbærgele) $=\frac{1}{8}\cdot \frac{2}{7}+\frac{2}{8}\cdot \frac{1}{7}=\frac{2}{56}+\frac{2}{56}=\frac{1}{14}=7,1$ %

Det er 7,1% sannsynlig at hun trekker en blåbær og en kiwigele.

e)

Volumet av melisen i prismet: $V=l\cdot b\cdot h=8cm\cdot 6cm\cdot 16cm=768c{m}^3=0,768d{m}^3=0,768liter=7,68desilliter$

Volumet av pakken er 0,768 liter.

Volumet av sylinderformet boks er :

$V=\pi r^{2}h=\pi \cdot (6cm{)}^2\cdot 10cm=360\pi c{m}^3\approx 1130c{m}^3=1,13d{m}^3=1,13liter$

Melisen vil få plass.

f)

Han har en fastlønn på 50 kr. per time. I tillegg tjener han 5 kr. per kg. moreller han plukker. Dette ser man fordi grafen krysser y aksen i 50 kr. og for hver kg. vi går bortover på x-aksen stiger grafen med 5 enheter på y - aksen.

g)

Proporsjonalitet: $y=kx$

Dersom to størrelser er proporsjonale vil den ene øke når den andre øker. Forholdet mellom dem er konstant.

Omvendt proporsjonalitet: $y=\frac{k}{x}$

Dersom to størrelser er omvendt proporsjonale vil den ene bli mindre når den andre øker. Produktet av to omvendt proporsjonale størrelser er konstant.

Rektanglene her har lengder og bredder som er omvendt proporsjonale. Arealet er konstant.

h)

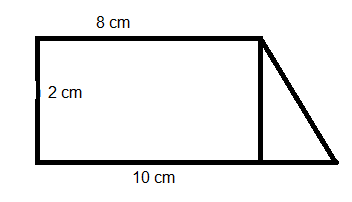
Areal av trapes :

$$\begin{gathered} A=\frac{a+b}{2}\cdot h \\ A=\frac{8cm+10cm}{2}\cdot 2cm=18c{m}^2 \end{gathered}$$

a og b er lengden av de parallelle sidene.

Oppgave 2:

a)

Et annuitetslån er et lån der du betaler et fast beløp hver måned som dekker både renter og avdrag. I begynnelsen går mesteparten til å dekker renter. Etter som tiden går, går mer og mer av det månedlige beløpet til å dekke avdrag. Et annuitetslån er normalt noe dyrere enn et serielån fordi man betaler noe for muligheten til å kunne betale samme beløpet hver termin.

Et serielån har faste avdrag og renteutgiftene er høyest i begynnelsen av låneperioden. Belastningen økonomisk blir derved størst i begynnelsen og det passer normalt dårlig for unge mennesker i etableringsfasen. dersom du har råd er imidlertid denne kontrakten normalt billigere enn annuitetslån.

b)

Fordi han bealer avdrag på kr. 10.000 per år. 10% av 10.000kr er 1000 kr. Lånet blir 10.000kr mindre hvert år.

c)

Fra Figuren ser det ut som terminbeløpet på anuitetslånet er ca. 16.200kr. Dvs, den titale tilbakebetalingen er 162.000 kroner.

20 +19 +18 +17 + 16 +15 +14 +13 +12 + 11 = 155

Dvs serielånet koster 55 tusen kroner. Jonas må betale 55 tusen pluss lånebeløpet på 100 tusen tilbake, dvs. totalt 155.000 kroner

Anuitetslånet blir dyrerer for nedbetalingene i starten er lavere (avdragene).

DEL TO

Oppgave 3:

a)

Bruker pytagoras og får:

$BD=\sqrt{7^2+5^2{m}^2}=\sqrt{74}m\approx 8,60m$

b)

Det kvadrattallet, K, som ligger nærmest 74, er 81.

$\sqrt{T}=\frac{1}{2}(\sqrt{K}+\frac{T}{\sqrt{K}})=\frac{1}{2}(\sqrt{81}+\frac{74}{\sqrt{81}})=\frac{155}{81}\approx 8,61$

Tilnærmingen er god for mange formål.

Oppgave 4:

a)

Volum liten kake: $V=\pi r^{2}h=\pi \cdot (10cm{)}^2\cdot 7cm=2199c{m}^3$

Volum medium kake: $V=\pi r^{2}h=\pi \cdot (13cm{)}^2\cdot 7cm=3717c{m}^3$

Volum stor kake: $V=\pi r^{2}h=\pi \cdot (15cm{)}^2\cdot 7cm=4948c{m}^3$