Løsning del 2 utrinn Vår 14

Oppgave 1

a)

$125\mathrm{kr}+105\mathrm{kr}+105=335\mathrm{kr}$

b)

Pris 25 enkeltbilletter:$25\cdot 125\mathrm{kr}=3125\mathrm{kr}$

Pris 1 klippekort à 25 klipp: $2665\mathrm{kr}$

Prisforskjell: $3125\mathrm{kr}-2665\mathrm{kr}=460\mathrm{kr}$

Anne sparer $\frac{460\mathrm{kr}}{3125\mathrm{kr}}=0,147=14,7\mathrm{\%}$

c)

Sum betalt: $2060\mathrm{kr}+910\mathrm{kr}+12\cdot 105\mathrm{kr}=4230\mathrm{kr}$

Gjennomsnitt per svømmetur: $\frac{4230\mathrm{kr}}{25+10+12}=\frac{4230\mathrm{kr}}{47}=90\mathrm{kr}/\mathrm{tur}$

Oppgave 2

a)

Til første bane kan vi velge blant 8 svømmere (8 muligheter). Til andre bane kan vi velge blant 7, osv helt til vi har igjen 1 svømmer som plasseres i den siste banen. Totalt antall kombinasjoner blir da $8\cdot 7\cdot 6\cdot 5\cdot 4\cdot 3\cdot 2\cdot 1=40320$.

b)

Eva svømmer med gjennomsnittsfarten $v=\frac{100\mathrm{m}}{100\mathrm{s}}=1\mathrm{m}/\mathrm{s}$. Etter $80\mathrm{s}$ er Anne i mål. Da har Eva bare svømt strekningen $s=1\mathrm{m}/\mathrm{s}\cdot 80\mathrm{s}=80\mathrm{m}$ (mens Anne har svømt de 100 metrene til mål). Eva vinner altså med $20\mathrm{m}$.

(I denne oppgaven må vi forutsette at de svømmer med konstant fart lik gjennomsnittsfarten.)

Oppgave 3

a), b)

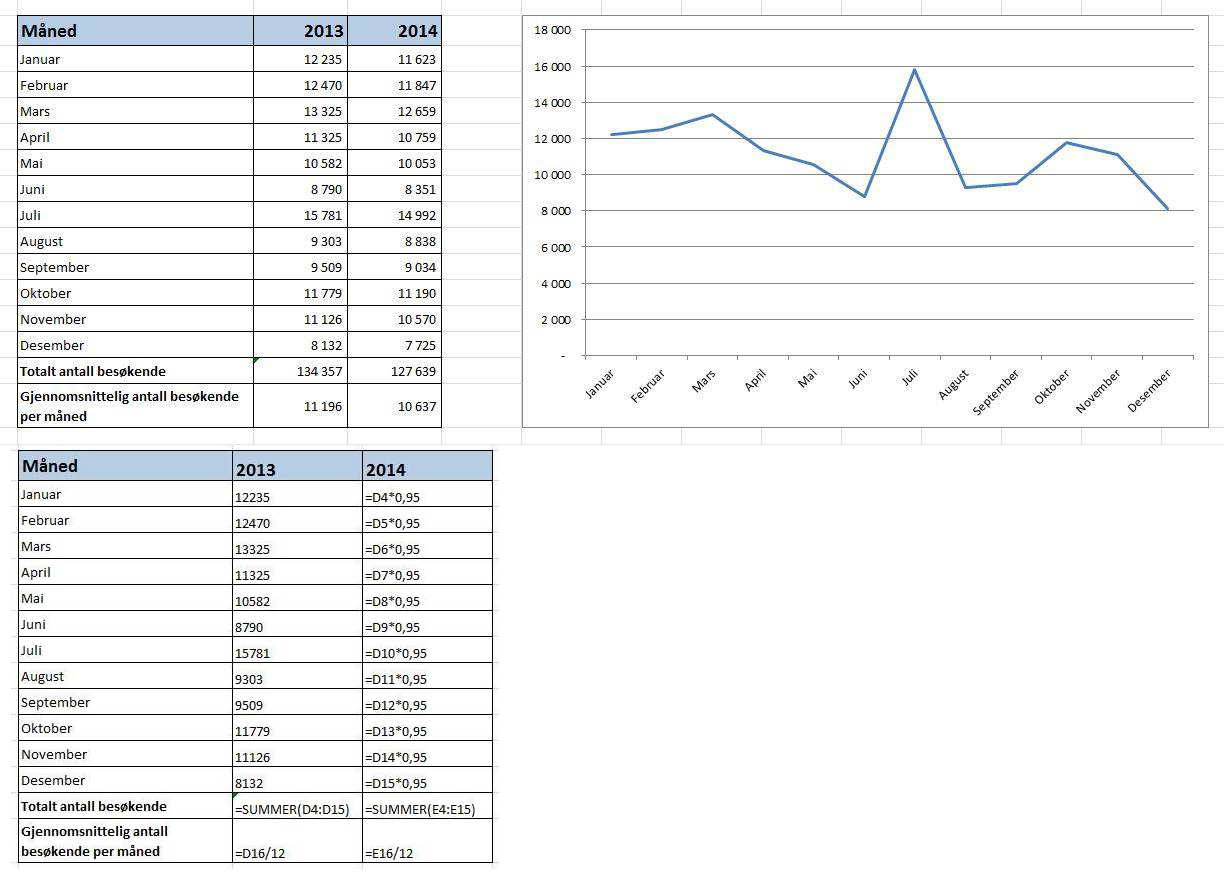
Se utklipp fra Excell under, diagram skal ha overskrift og akser skal ha navn, bruk av fast cellereferanse i oppgave c viser bedre kompetanse;

Oppgave 4

a)

Tegn et rektangel der lengden/den lengste siden er 10 cm og bredden/den korteste siden er 5 cm.

b)

Hele bassengets lengde er 25 m. Det betyr avstanden fra A til B horisontalt er $25\mathrm{m}-12,5\mathrm{m}-6,25\mathrm{m}=6,25\mathrm{m}.$. Høydeforskjellen mellom AB blir på tilsvarende måte $3,5\mathrm{m}-1,2\mathrm{m}=2,3\mathrm{m}$. Da gir Pytagoras' setning skråplanets lengde AB:

$(AB{)}^2=(6,25\mathrm{m}{)}^2+(2,3\mathrm{m}{)}^2$

$AB=\sqrt{44,35{\mathrm{m}}^2}$

$AB=6,66\mathrm{m}$

c)

Se for deg en vegg rett opp gjennom AD og en tilsvarende vegg ved BC. Kall bassenget/volumet lengst til venstre $V(1)$, det i midten $V(2)$ og det lengst til høyre $V(3)$. Regn ut disse volumene hver for seg, og summer dem til slutt:

$V(1)=6,25\mathrm{m}\cdot 12,5\mathrm{m}\cdot 3,5\mathrm{m}=273,44{\mathrm{m}}^3$

$V(2)=6,25\mathrm{m}\cdot 12,5\mathrm{m}\cdot 3,5\mathrm{m}-\frac{1}{2}\cdot 6,25\mathrm{m}\cdot 12,5\mathrm{m}\cdot 2,3\mathrm{m}=183,59{\mathrm{m}}^3$

$V(3)=12,5\mathrm{m}\cdot 12,5\mathrm{m}\cdot 1,2\mathrm{m}=187,50{\mathrm{m}}^3$

$V_{totalt}=V(1)+V(2)+V(3)=273,44{\mathrm{m}}^3+183,59{\mathrm{m}}^3+87,50{\mathrm{m}}^3=644,5{\mathrm{m}}^3$

d)

Etter en time (60 min) har det blitt tappet ut

$300\mathrm{L}/\min \cdot 60\min =18000\mathrm{L}=18{\mathrm{m}}^3$ vann. Dette er mindre enn volumet av det øverste sjiktet med vann (mindre enn volumet av vannet over skråplanet). Vi kan dermed sette opp likningen

$18{\mathrm{m}}^3=25\mathrm{m}\cdot 12,5\mathrm{m}\cdot h$

$h=\frac{18}{25\cdot 12,5}\mathrm{m}=0,058\mathrm{m}$,

Vannstanden har altså sunket 5,8 cm ned etter én time.

Oppgave 5

a)

Vi får et konstantledd på $+645000$ da dette er volumet vann ved start ($x=0$). Dessuten får vi et negativt førstegradsledd, $-1800x$. Dette skyldes at volumet minker med 18000 liter hver time.

b)

Tomt for vann når $V(x)=0$. Det gir:

$0=-18000x+645000$

$18000x=645000$

$x=\frac{645000}{18000}\mathrm{h}=35,83\mathrm{h}=35\mathrm{h}$ $50\min$

c)

Bruker Geogebra (Versjon 4.2). I inntastingsfeltet (nederst) bruker vi kommandoen:

"Funksjon[ <Funksjon>, <Start>, <Slutt> ]"

Helt konkret taster vi inn:

"Funksjon[-18000x + 645000, 0, 36]"

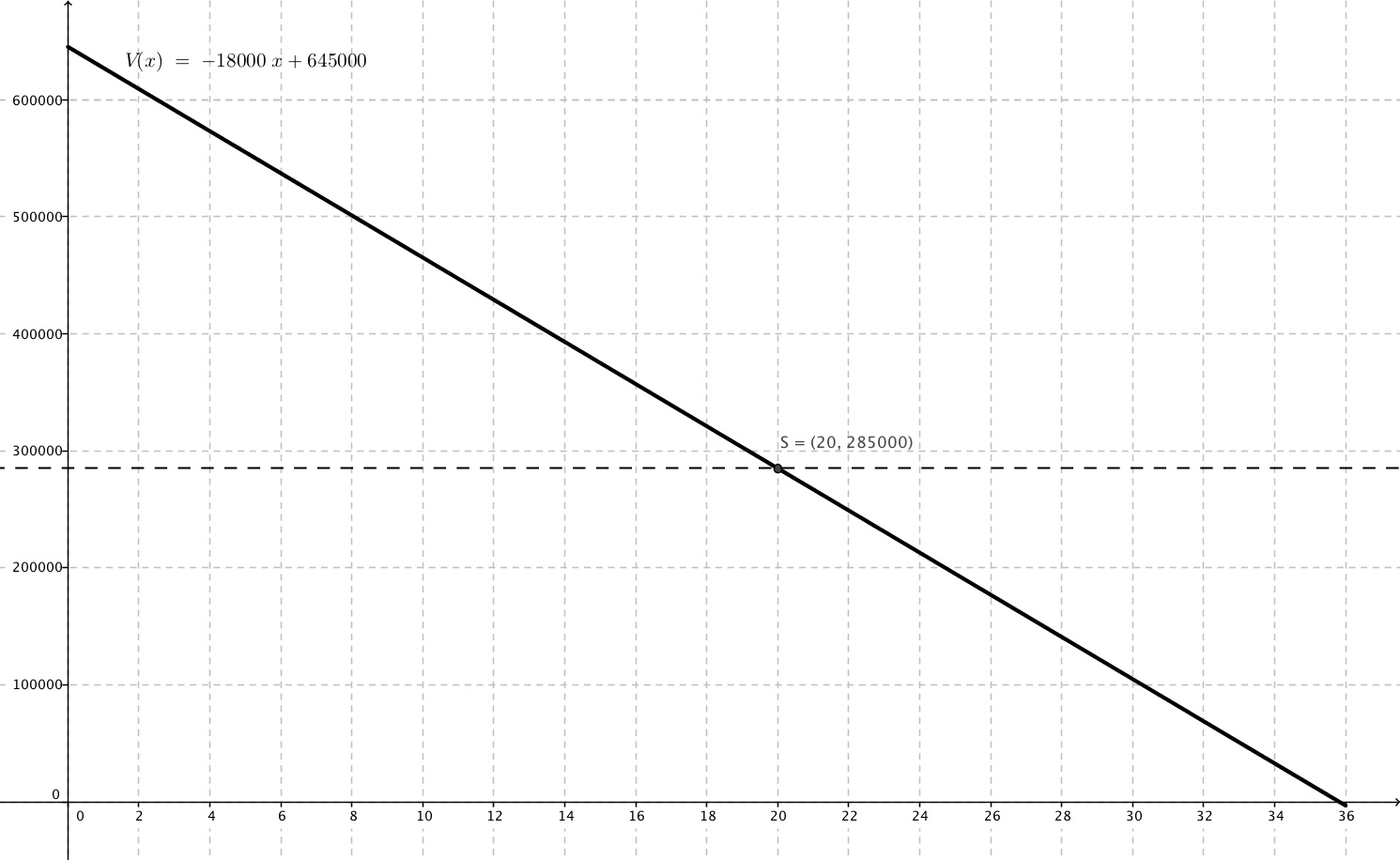
Funksjonen blir da hetende f. Høyreklikker på funksjonen i algebrafeltet og gir den nytt navn; V. Grafen blir seende ut som på figuren i deloppgave d) under.

d)

I inntsatingsfeltet skriver vi "y=285000". Deretter finner vi skjæring mellom de to linjene. Bruker da verktøyet "Skjæring mellom to objekt" fra menylinjen, og klikker deretter på de to linjene. Vi får skjæringspunktet $S$ med $x$-koordinat 20, se figur under. Det tar altså 20 timer før bassengets volum er 285 000 liter.

$x$-aksen er tiden målt i timer. $y$-aksen antall liter i bassenget.

Oppgave 6

a)

Radius, $r$, er halve diameteren, $d$. Omkretsen, $O$, er gitt ved $O=d\pi$. Vi får

$r_{adius}=\frac{d}{2}=\frac{12.756\mathrm{km}}{2}=6378\mathrm{km}$

$O_{omkrets}=d\pi =12.756\mathrm{km}\cdot 3,14=40053,8\mathrm{km}$

b)

${\mathrm{\angle }}_{søyle,solstråle}=\frac{{360}^{\circ }}{50}=7,2^{\circ }$

c)

$A_{vstand}=5000$ $\mathrm{stadion}=5000\cdot 157,5\mathrm{m}=787.500\mathrm{m}=767,5\mathrm{km}$

d)

For å finne overflaten av jorda, bruker formelen $O=4\pi r^2$, med radien $r$ regnet ut i deloppgave a). For å finne overflaten som er dekket med vann, må vi gange denne formelen med $0,71$, ettersom kun $71\mathrm{\%}$ av overflaten er dekket med vann. Den totale formelen blir da:

$O_{verflate(vann)}=0,71\cdot 4\pi r^2=2,84\cdot 3,14\cdot {6378}^2{\mathrm{km}}^2=362942012{\mathrm{km}}^2=3,63\cdot {10}^8$ ${\mathrm{km}}^2$

Oppgave 7

a)

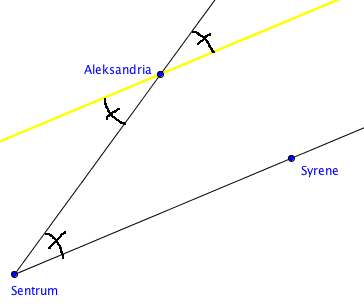
Solstrålene som treffer jorda er parallelle. Solstrålen som går gjennom brønnen, peker rett inn mot sentrum i jorda. Det betyr at linjen fra sentrum av jorda ut til sola, er parallell med solstrålen som kaster skygge bak søylen. Videre krysser linjen mellom jordsenteret og søylen, begge de to parallelle linjene. Dermed må vinklene bli like store. Se en forenklet figur under. Alle tre vinklene på figuren er like store, fordi to av linjene er parallelle, mens den tredje skjærer dem begge.

b)

Vi husker fra oppgave 6 b) at vinkelen mellom solstrålen og søylen, og dermed også vinkel A, er $7,2^{\circ }$. Dette betyr at de 5 000 stadionlengdene mellom byene, kun er $\frac{7,2}{360}=0,02=2\mathrm{\%}$ av jordas totale omkrets. For å finne hele jordas omkrets, må vi gange med 50 slik at vi får $100\mathrm{\%}$. Vi får

$O_{mkrets}=5.000$ $\mathrm{stadion}\cdot 50=250.000$ $\mathrm{stadion}$

NB Det finnes alternative løsninger.

Oppgave 8

På grunn av toppvinkler og samsvarende vinkler som dannes av de parallelle linjene (solstrålene) får vi (18° + 26°)=44°

(44°*39375 km)/(360°)≈4812 km

Avstanden fra A til B er 4812 km