Løsning del 1 utrinn Vår 15 eksempeloppgave

Oppgave 1

a) $987+589=1576$

b) $8643-4789=3854$

c) $345\cdot 678=233910$

d) $32:0.64=50$

Oppgave 2

a) $205\text{min}=3\text{h}25\text{min}$

b) $8000\text{mg}=0.008\text{kg}$

c) $750\text{mL}=0.75\text{L}$

d) $1\text{daa (dekar)}=1000m^2$

$11500m^2=11.5\cdot 1000m^2=11.5\text{daa (dekar)}$

Oppgave 3

a) $\frac{3}{10}\cdot 15=\frac{3\cdot 15}{10}=\frac{45}{10}=\frac{9}{2}=4\frac{1}{2}$

b) $6:\frac{3}{4}=6\cdot \frac{4}{3}=\frac{6\cdot 4}{3}=\frac{24}{3}=8$

Oppgave 4

a) $1+2\cdot (3-4{)}^2=3$

b) $-5\cdot (-2+4{)}^2-\frac{2^3}{4}=-22$

Oppgave 5

a) $x+3=-3x+7$

$x+3x+3=7$

$x+3x=7-3$

$4x=4$

$x=1$

b) $\frac{x}{6}-\frac{2-x}{4}=\frac{x}{3}+1$

$\frac{x}{6}-(\frac{2}{4}+\frac{-x}{4})=\frac{x}{3}+1$

$\frac{x}{6}-(\frac{2}{4}-\frac{x}{4})=\frac{x}{3}+1$

$\frac{x}{6}-\frac{2}{4}+\frac{x}{4}=\frac{x}{3}+1$

$\frac{x}{6}+\frac{x}{4}=\frac{x}{3}+1+\frac{2}{4}$

$\frac{x}{6}+\frac{x}{4}-\frac{x}{3}=1+\frac{2}{4}$

$\frac{x}{6}\cdot 12+\frac{x}{4}\cdot 12-\frac{x}{3}\cdot 12=1\cdot 12+\frac{2}{4}\cdot 12$

$x\cdot 2+x\cdot 3-x\cdot 4=12+2\cdot 3$

$x=18$

Oppgave 6

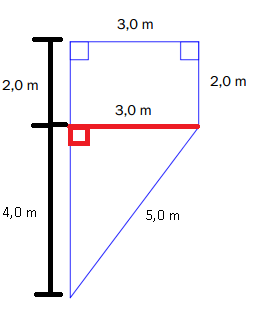
Deler opp figuren i et rektangel og en trekant. Trekanten er rettvinklet, og har to kateter med sider 3 m og 4 m. Kan derfor bruke pythagoras for å finne den ukjente siden.

${3.0}^2+{4.0}^2=x^2$

$9.0+16.0=x^2$

$25.0=x^2$

$5.0=x$

$x=5.0$

Hypotenusen er 5.0 m.

Finner så omkretsen: $6.0m+3.0m+2.0m+5.0m=16.0m$

Hjelpetegning:

Oppgave 7

a) Én T-skjorte koster $100$ kroner. Det vil si at 3 T-skjorter normalt ville kostet $300$ kroner. Men ettersom jeg benytter meg av tilbudet ta tre, betal for to, så betaler jeg kun 200 kr. Avslaget jeg får er $300-200=100kr$. Finner så hvor mange prosent 100 kr er av 300 kr.

$\frac{100kr}{300kr}=0.33=33\mathrm{\%}$

Jeg får $33\mathrm{\%}$ avslag.

b) Pondus har fått 5 flasker sjampo og bare betalt for 2 flasker sjampo. Pondus har altså fått $5-2=3$ flasker i avslag.

$\frac{3\text{flasker}}{5\text{flasker}}=0.6=60\mathrm{\%}$

Pondus har fått $60\mathrm{\%}$ avslag.

Oppgave 8

a) Hva er ${86}^o$ Fahrenheit i Celsius? Bruker formelen $C=\frac{5}{9}\cdot (F-32)$

$C=\frac{5}{9}\cdot ({86}^{o}F-32)={30}^{o}C$

${86}^o$ Fahrenheit tilsvarer ${30}^o$ Celsius

b) $C=\frac{5}{9}\cdot (F-32)$

$\frac{9}{5}\cdot C=F-32$

$\frac{9}{5}\cdot C+32=F$

$F=\frac{9}{5}\cdot C+32$

Oppgave 9

a)

$\frac{4x^2}{2x}=\frac{2\cdot \bcancel{2}\cdot x\cdot \bcancel{x}}{\bcancel{2}\cdot \bcancel{x}}=2x$

b)

$\frac{5x + 25}{x^2 -25} = \frac{5x + 5 \cdot 5}{x^2 -5^2} = \frac{5\bcancel{(x + 5)}}{(x-5)\bcancel{(x+5)}} = \frac{5}{x-5}