Trigonometri R2: Forskjell mellom sideversjoner
Ny side: ==Trigonometeriske funksjoner== Den viktigste trigonometeriske funksjonen er sinusfunksjonen. Alle de andre trigonometeriske funksjonene kan utledes fra denne. Sinusfunksjonen defineres sl... |
Ingen redigeringsforklaring |
||
| Linje 1: | Linje 1: | ||
==Radianer== | |||
Radianer (også kalt absolutt vinkelmål) er definert ved at <tex>360^\circ = 2\pi\</tex> radianer. | |||
==Trigonometeriske funksjoner== | ==Trigonometeriske funksjoner== | ||
| Linje 14: | Linje 18: | ||
[[Bilde:Trig2.png]] | [[Bilde:Trig2.png]] | ||
Sinus- og cosinuskurvene har begge perioder på <tex>2\pi</tex> radianer. | |||
===Definisjon av tan(x)=== | ===Definisjon av tan(x)=== | ||
| Linje 20: | Linje 26: | ||
<tex>\tan\,x=\frac{\sin\,x}{\cos\,x}</tex> | <tex>\tan\,x=\frac{\sin\,x}{\cos\,x}</tex> | ||
Når vi plotter tangenskurven, ser den slik ut: | |||
[[Bilde:Trigtan.png]] | |||
Tangenskurven har en periode på <tex>\pi</tex> radianer. | |||
Sideversjonen fra 18. jan. 2010 kl. 18:28
Radianer
Radianer (også kalt absolutt vinkelmål) er definert ved at <tex>360^\circ = 2\pi\</tex> radianer.
Trigonometeriske funksjoner
Den viktigste trigonometeriske funksjonen er sinusfunksjonen. Alle de andre trigonometeriske funksjonene kan utledes fra denne. Sinusfunksjonen defineres slik:
Definisjon av sin x og cos x
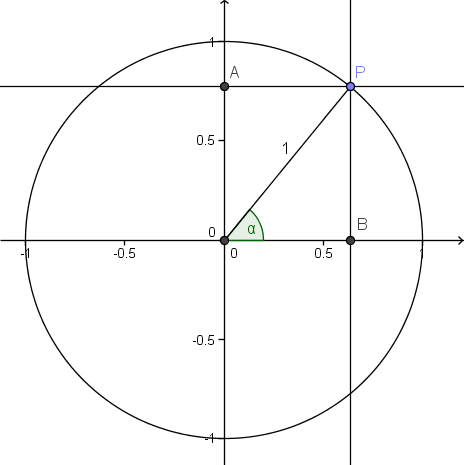
Ta utgangspunkt i figuren under:
Når vi konstruerer en enhetssirkel og en radius med vinkel <tex>\alpha</tex> på x-aksen slik figuren viser, vil radien skjære sirkelperiferien i punktet <tex>P</tex>. Hvis trekker normalene fra <tex>P</tex> på koordinataksene, vil de skjære disse i punktene <tex>A</tex> og <tex>B</tex> slik figuren viser. Da vil y-verdien til punktet <tex>A</tex> være lik <tex>\sin\,\alpha</tex> og x-verdien til punktet <tex>B</tex> være lik <tex>\cos\,\alpha</tex>
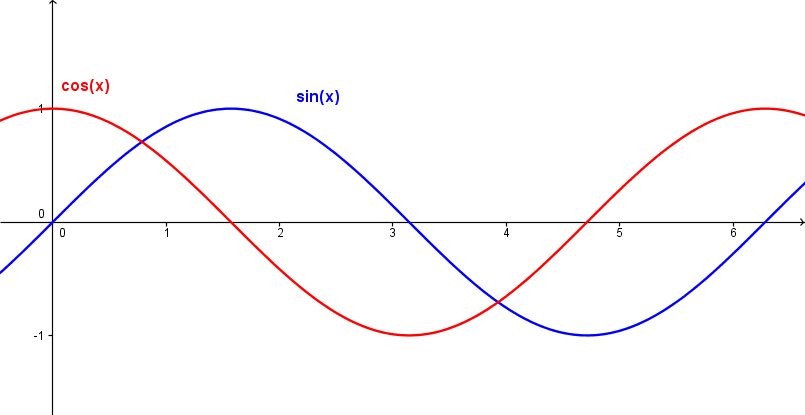
Når vi plotter sinus- og cosinuskurvene ser de slik ut:
Sinus- og cosinuskurvene har begge perioder på <tex>2\pi</tex> radianer.
Definisjon av tan(x)
Tangensfunksjonen er definert slik at
<tex>\tan\,x=\frac{\sin\,x}{\cos\,x}</tex>
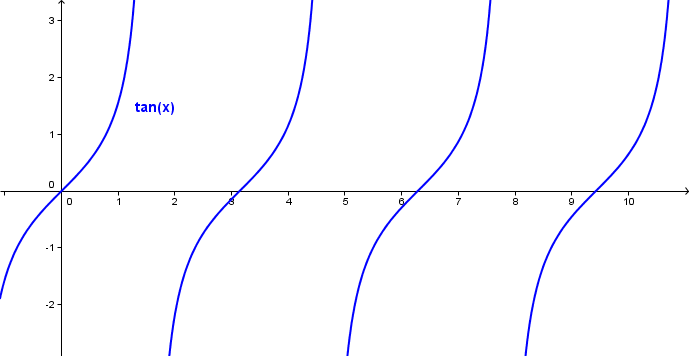
Når vi plotter tangenskurven, ser den slik ut:
Tangenskurven har en periode på <tex>\pi</tex> radianer.