1T 2015 vår LØSNING: Forskjell mellom sideversjoner
| Linje 163: | Linje 163: | ||
===b)=== | ===b)=== | ||
[[File:1t-v15-12bc.png]] | |||
===c)=== | ===c)=== | ||
Sideversjonen fra 8. jul. 2015 kl. 09:35
Løsning laget av mattepratbruker LektorH
DEL EN
Oppgave 1
$\frac{7,5 \cdot 10^{15}}{0,003} \\= \frac{7,5}{3} \cdot 10^{15+3} \\ = 2,5 \cdot 10^{18}$
Oppgave 2
<math> \left[ \begin{align*}x+6y=1 \\ 2x+4y=-6 \end{align*}\right] </math>
<math> \left[ \begin{align*} x= 1-6y \\ 2(1-6y)+4y=-6\end{align*}\right] </math>
<math> \left[ \begin{align*} x= 1-6y \\ 2-12y+4y= -6 \end{align*}\right] </math>
<math> \left[ \begin{align*} y=1 \end{align*}\right] </math>
Innsatt i første likning gir det x=-5, dvs:
$x= -5 \wedge y= 1$
Oppgave 3
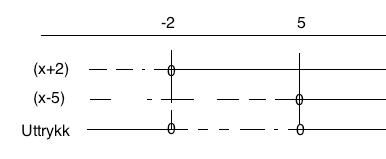
$x^2-3x-10 >0$
Løser andregradslikningen: $x^2-3x-10=0 \\ x= \frac{3 \pm \sqrt{9+40}}{2} \\ x= \frac{3 \pm 7}{2} \\ x= -2 \vee x= 5$
Vi observerer at uttrykket skulle være større enn null: $x \in < \leftarrow, -2> \cup <5, \rightarrow>$
Oppgave 4
a)
$4^{\frac12} \cdot 8^0 \cdot 2^{-1} \cdot \sqrt[4]{16} \\ = 2 \cdot 1 \cdot 0,5 \cdot 2 \\=2 $
b)
$\sqrt{18}\cdot \sqrt 2 + \frac{\sqrt{72}}{\sqrt 8} \\= \sqrt{18 \cdot 2} + \sqrt{\frac{72}{8}} \\ = 6+3=9$
Oppgave 5
$lg(x^2-0,9) = -1 \\ 10^{lg(x^2-0,9)} = 10^{-1} \\ x^2- 0,9 = 0,1 \\ x^2 =1 \\x = \pm 1$
Vi kan ikke ta logaritmen til et negativt tall, og ma sjekke begge løsningene. I dette tilfellet kan begge løsninger brukes:
$x= - 1 \vee x=1$
Oppgave 6
$x^2+bx+16$
Vi registrerer at $16 = (\pm4)^2 $. Da må b vare lik det dobbelte av $\pm 4$, i følge kvadratsetningene.
$x^2 \pm 8x+16 = (x \pm4)^2$
b er altså lik $ \pm8$
Oppgave 7
$2x(x-2)-(x-2)(2x+1) \\ = 2x^2 -4x- ( 2x^2+x-4x-2) \\= 2x^2 -4x-2x^2-x+4x+2 \\ = -x+2$
Oppgave 8
$\frac{x^2-12x+36}{2X^2 - 72} \\= \frac{(x-6)(x-6)}{2(x+6)(x-6)} \\ =\frac{x-6}{2(x+6)}$
Oppgave 9
En rett linje har likningen :
y = ax + b
Stigningstall er: a = $\frac{\Delta y}{ \Delta x} = \frac {4-2}{3-(-1)} = \frac 12$
Bruker x og y verdi i første punkt og finner b:
$2 = \frac 12 \cdot -1 + b \\ b = \frac 52$
$y= \frac 12x + \frac 52$
Oppgave 10
a)
Bruker Pytagoras på trekant ABC og får:
AB = $\sqrt{2^2-1^2} = \sqrt 3$
Bruker Pytagoras på trekant DEF og får:
DF = $\sqrt{1^2 + 1^2} = \sqrt 2$
b)
Cosinus til en vinkel er hossliggende katet delt på hypotenus.
Sinus til en vinkel er motstående katet delt på hypotenus.
Tangens til en vinkel er motstående katet delt på hossliggende katet.
| u | sin u | cos u | tan u |
| $30^{\circ}$ | $\frac 12$ | $\frac{\sqrt 3}{2}$ | $\frac{1}{\sqrt 3}$ |
| $45^{\circ}$ | $\frac{\sqrt 2}{2}$ | $\frac{\sqrt 2}{2}$ | 1 |
| $60^{\circ}$ | $\frac{\sqrt 3}{2}$ | $\frac 12$ | $\sqrt 3$ |
Oppgave 11
a)
Trekker to, sannsynnlighet for ikk e "Jump":
P( ikke Jump) = $xx$
b)
c)
Oppgave 12
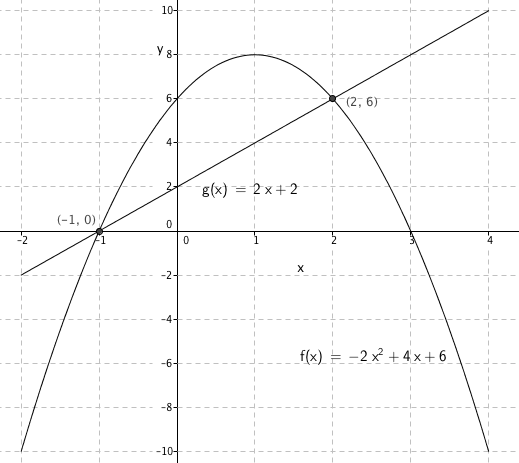
$f(x)= -2x^2+4x+6$
a)
b)
c)
Oppgave 13
Jordens radius er r, og omkretsen er O.
$O = 2\pi r$
Dersom vi forlenger tauet med 20 meter blir ny omkrets: O + 20. Vi må da finne tillhørende radius.
$r= \frac{O}{2 \pi}$
Ny radius blir:
$r_{20} = \frac{O+20}{2 \pi} = \frac{O}{2 \pi} + \frac{10}{\pi} $
Tauet vil være ca. 3 meter over bakkenivå så det vil være mulig å gå under tauet.