2P 2016 vår LØSNING

Diskusjon av denne oppgaven på matteprat

Del 1 Løsningsforslag laget av mattepratbruker jøgge

Del 2 Løsningsforslag laget av mattepratbruker jøgge

Løsningsforslag fra mattepratbruker Oyan

DEL EN

Oppgave 1)

-6, -4, 0, 2, 2, 6.

Variasjonsbredde: 6 - ( - 6 ) = 12

Variasjonsbredden er 12 grader.

Median: $\frac{0+2}{2}=1$

Median er 1 grad.

Gjennomsnitt: $\frac{-6+(-4)+0+2+2+6}{6}=\frac{0}{6}=0$

Gjennomsnittsteperaturen denne perioden er null grader celsius.

Oppgave 2)

Forutsetter at en måned er 30 dager.

$$\begin{gathered} 7500000000\cdot 2\cdot 30= \\ 7,5\cdot {10}^9\cdot 6,0\cdot 10= \\ 7,5\cdot 6,0\cdot {10}^{10}= \\ 45\cdot {10}^{10}=4,5\cdot {10}^{11} \end{gathered}$$

Oppgave 3)

Ptis bukse i butikk A: 150 kr, og i butikk B: 120 kr.

a)

$\frac{150-120}{120}=\frac{1}{4}=25$%

Buksene er 25% dyrere i butikk A, i forhold til i butikk B.

b)

$\frac{150-120}{150}=\frac{1}{5}=20$%

Buksene er 20% billigere i butikk B, i forhold til i butikk A.

Oppgave 4)

Pris på jakke uten MVA:

$$\begin{gathered} x\cdot 1,25=750 \\ x=\frac{750}{1,25}=600 \end{gathered}$$

Jakken koster 600 kroner uten MVA, altså er merverdiavgiften 150 kroner.

Oppgave 6)

a)

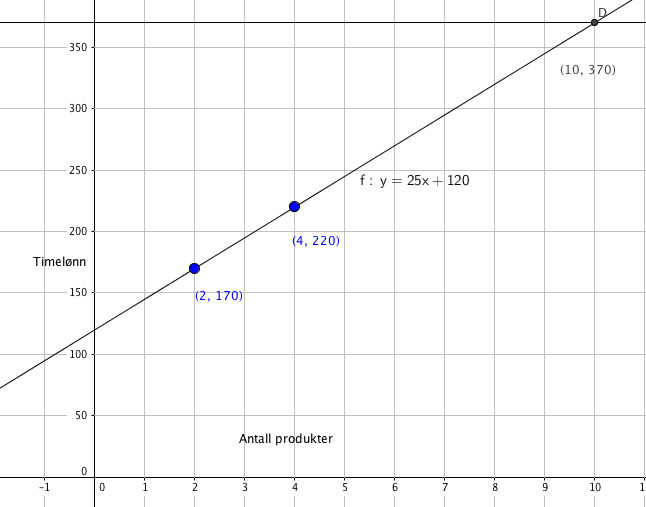
Vi plotter punktene i et koordinatsystem og trekker en rett linje. Denne linjen skjærer y aksen i 120, og stiger med 25 for hver enhet mot høyre på x-aksen.

y-aksen er timelønn og x-aksen er antall enheter.

b)

Den rette linjen i a har uttrykket y = 25x + 120.

Det betyr at fastlønna er 120 kroner og at hun i tillegg tjener 25 kroner for hvert produkt hun selger.

c)

Fra grafen i a ser man at hun må selge 10 produkter.

Oppgave 7)

a)

Dersom noe øker eksponentielt betyr det at det vokser med en fast prosent hver tidsperiode.

b)

b er eneste kurve som oppfuller kravet i a. c vokser lineært, altså med en fast størrelse hver tidsperiode. a vokser mindre etter en stund, noe som kan minne om logistisk vekst (ikke pensum i 2P).

Oppgave 8)

Skriver alle tallene på standardform:

$$\begin{gathered} 0,046\cdot {10}^{11}=4,6\cdot {10}^9 \\ \frac{46}{1000000}=0,000046=4,6\cdot {10}^{-5} \\ 46\cdot {10}^{-7}=4,6\cdot {10}^{-6} \\ 4600000=4,6\cdot {10}^6 \\ 4,6\cdot {10}^8 \\ 0,46\cdot {10}^{-6}=4,6\cdot {10}^{-7} \end{gathered}$$

Faktoren 4,6 går igjen i alle tallene og vi kan sortere etter størrelse ved å se på eksponenten i tierpotensen:

I stigende rekkefølge: ${10}^{-7},{10}^{-6},{10}^{-5},{10}^6,{10}^8,{10}^9.$

DEL TO

Oppgave 4

a)

Figur	Ant. hvite rektangler	ant. blå rektangler	Ant. rektangler totalt
1	1	8	9
2	4	12	16
3	9	16	25
4	16	20	36
n	$n^2$	$4n+4$	$n^2+4n+4$

b)

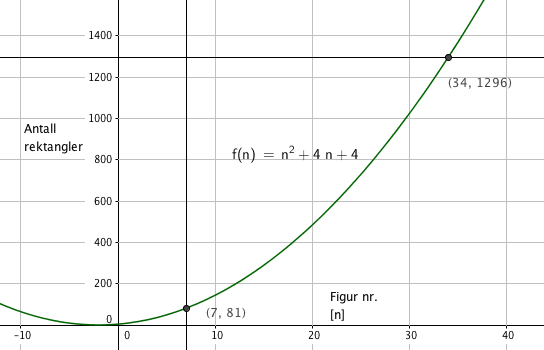
9 ganger 9 er 81, altså blir det figur nr 7 (n + 2) , det betyr at man trenger $7^2=49$ hvite rektangler.

c)

Bruker Figuren laget i Geogebra til å finne at det er snakk om figur nr 34. Antall blå rektangler blir da $4\cdot 34+4=140$

Oppgave 7

a)

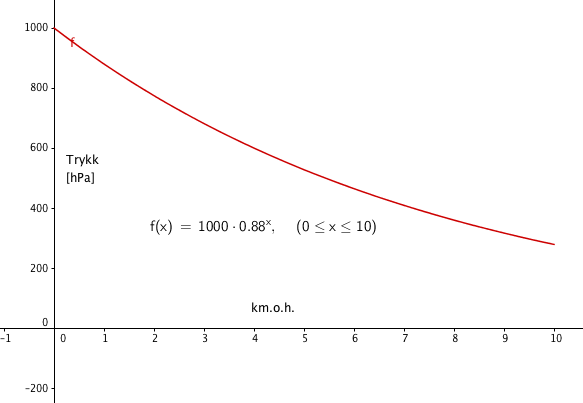
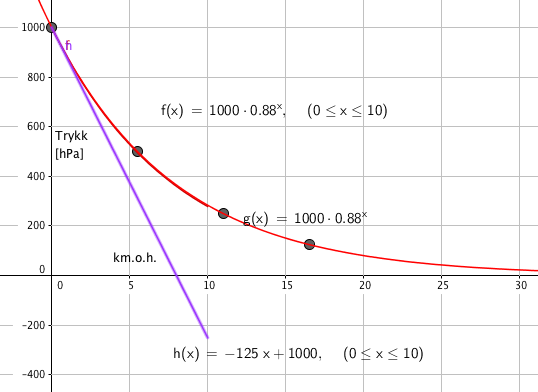
Siden trykket avtar med en fast prosent per km er dette eksponentiell vekst (om enn negativ) med vekstaktor 1 - 0,12 = 0,88. Desom vi i tillegg til sitat 1 inkluderer informasjone om lufttrykket ved havets overflate kan vi sette opp modellen:

$f(x)=1000\cdot 0,{88}^x$

Der x er kilometer over havets overflate.

b)

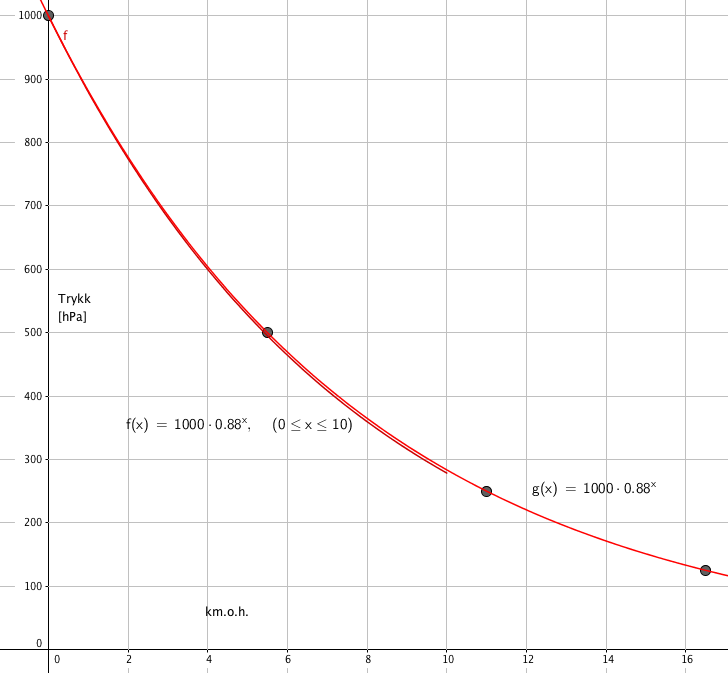
Lufttrykket halveres for hver 5,5 km opp fra havoverflaten

Vi observerer at den eksponentielle tilpassningen gir en modell praktisk talt lik den i a.

c)

Dette er en lineær modell som trolig virker bra til en hvis høyde over havet. Store høyder gir trolig store feil.

For å finne hvor mye trykket avtar per 1000 meter tar vi 1000:8 = 125 (hPa)

h(x)= -125x + 1000

Som vi antok er denne modellen kun gyldig i et lite begrenset område rett over havflaten.

d)

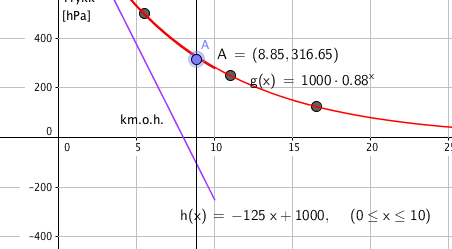
Modell h er ubrukelig fordi høhden over havet er stor, den gir et negativt trykk??

Moddell f og g er i praksis like og gir et et romelig svar, 316 hPa.