Integrasjon: Forskjell mellom sideversjoner
| Linje 142: | Linje 142: | ||
Merk at integrasjonskonstanten blir kansellert når <math>F(x)</math> brukes i sammenheng med det bestemte integralet. Det viser at verdien til <math>C</math> er vilkårlig. | Merk at integrasjonskonstanten blir kansellert når <math>F(x)</math> brukes i sammenheng med det bestemte integralet. Det viser at verdien til <math>C</math> er vilkårlig. | ||
==Integrasjon ved variabelskifte== | == 3.1...Integrasjon ved variabelskifte== | ||
I derivasjon sier kjerneregelen at | I derivasjon sier kjerneregelen at | ||
Sideversjonen fra 28. aug. 2016 kl. 14:13
3.2.1
I læren om integraler tas det i bruk noe mer avanserte konsepter enn man ellers finner i matematikken på videregående. Dette spesielt i forbindelse med definisjonene rundt integrasjon. Det er derfor viktig å beherske både funksjonslære, derivasjon og algebra før man gir seg i kast med integrasjonsdelen av R2-pensumet.
Integrasjon er en operasjon som tar en funksjon og gir en ny funksjon som beskriver arealet under den første funksjonen.
3.2.2
Det bestemte integralet
Med det bestemte integalet av en funksjon vil vi finne arealet under funksjonen avgrenset av <math>x</math>-aksen og linjene <math>x=a</math> og <math>x=b</math>. "Det bestemte integralet av <math>f(x)</math> fra <math>a</math> til <math>b</math>" skriver vi som
<math>\int_a^b f(x)\rm{d}x</math>
3.2.3
Bestemt integral som grenseverdi
Vi kan se for oss arealet under en graf som en sum av rektangler, der antallet rektangler angir nøyaktigheten av integralet.
Dersom vi vil integrere <math>f(x)</math> fra <math>x=a</math> til <math>x=b</math> med <math>n</math> rektangler, må hvert rektangel ha bredde <math>\Delta x=\frac{b-a}{n}</math> (vi deler avstanden mellom endepunktene, <math>b-a</math> på antallet rektangler <math>n</math>.) Vi får da at
<math>A=\sum_{i=0}^n f(a+i\Delta x)\cdot \Delta x=\sum_{i=0}^n f\left( a+i\frac{b-a}{n}\right)\frac{b-a}{n}</math>
Når vi lar <math>\Delta x</math> gå mot null, dvs at vi lar antallet rektangler <math>n</math> gå mot uendelig, får vi det nøyaktige arealet under kurven:
<math>\int_a^b f(x)\rm{d}x=\lim_{n\to\infty} \sum_{i=0}^n f\left( a+i\frac{b-a}{n}\right)\frac{b-a}{n}</math>
Ubestemt integrasjon
I analysen (engelsk: Calculus) finnes et fundamentalteorem som relaterer operasjonene integrasjon og derivasjon med hverandre. Dette gjør det mulig å finne integralet av funksjoner uten å regne ut kompliserte summer som ovenfor. Teoremet er delt inn i to deler, som ofte kalles analysens første og andre fundamentalteorem.
Analysens første fundamentalteorem sier at hvis en reell funksjon <math>F(x)</math> er definert på intervallet <math>[a,b]</math> ved
<math>F(x)=\int_a^x f(t)\rm{d}t</math>
der <math>f(t)</math> er en reell funksjon som er kontinuerlig på intervallet <math>[a,b]</math>, da er <math>F(x)</math> kontinuerlig på <math>[a,b]</math> og deriverbar på <math>(a,b)</math>, og man kan vise at <math>\frac{d}{dx}F(x)=f(x)</math>, og vi skriver at
<math>\int f(x)\rm{d}x=F(x)</math>
Analysens andre fundamentalteorem sier at
<math>\int_a^b f(x)\rm{d}x=F(b)-F(a)</math>
<math>F(a)-F(b)</math> er lik arealet mellom <math>x</math>-aksen og funksjonen <math>f(x)</math> mellom <math>x=a</math> og <math>x=b</math>.
Her skal vi vise geometrisk at <math>\frac{d}{dx}F(x)=f(x)</math>:
- Bevis: Den deriverte av den integrerte er funksjonen selv
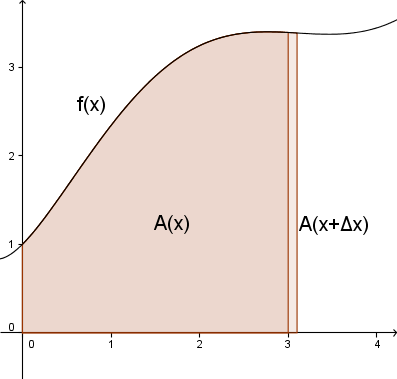
- La <math>f(x)</math> være en reell funksjon <math>(f(x)\in\mathbb{R}</math>, for alle <math>x\in \mathbb{R})</math>, og la funksjonen <math>A(x)</math> beskrive arealet mellom <math>x</math>-aksen og <math>f(x)</math> ved at <math>A(b)-A(a)</math> er lik arealet mellom <math>x</math>-aksen og <math>f(x)</math> mellom <math>x=a</math> og <math>x=b</math>. Mellom <math>x</math> og <math>x+\Delta x</math> vil aralet altså være <math>A(x+\Delta x)-A(x)</math>, se figur:
- I grenseverdien når <math>\Delta x\to 0</math> vil dette arealet bli tilnærmet et rektangel. Arealet av et rektangel er gitt ved
- <math>A=l\cdot b</math>
- og arealet at dette rektangelet ser vi ut ifra figuren blir <math>f(x)\cdot \Delta x</math>. Dermed kan vi konkludere at
- <math>f(x)=\lim_{\Delta x\to0}\frac{A(x+\Delta x)-A(x)}{\Delta x}</math>
- Men dette kjenner vi som definisjonen av den deriverte. Altså kan vi skrive at
- <math>f(x)=\frac{d}{dx}A(x)</math>
- Vi har dermed bevist at derivasjon og integrasjon er inverse operasjoner av hverandre, det vil si at
- <math>\frac{d}{dx}\int f(x)\rm{d}x=f(x)</math>
Dette kan også vises analytisk ved å ta i bruk noe mer avansert funksjonslære.
Når vi antideriverer en funksjon, dvs at vi tar det ubestemte integralet av funksjonen, får vi altså funksjonen <math>F(x)</math> som inngår i fundamentalteoremet.
Formler for integrasjon
Her er noen nyttige formler for integrasjonen av sentrale funksjoner. Med metodene i de neste seksjonene vil vi også kunne integrere funksjoner sammensatt av disse. Denne tabellen må læres utenat.
$\int f(x) dx = F(x)$
| f(x) | F(x) | Eksempel | |
| $x^n$ | $\frac{1}{n+1}x^{n+1} + C$ | $f(x)=x^3$ | $\int f(x) dx= \frac{1}{4}x^{4} + C$ |
| $ \frac 1x$ | ln x + C | x er positiv | |
| $e^x$ | $e^x +C $ | ||
| $a^x$ | $\frac{1}{ln a} a^x + C$ | ||
| cos x | sin x + C | ||
| sin x | - cos x + C |
Bestemte integgraler
$\int\limits_a^a f(x)dx =0 \\ \int\limits_a^b kf(x)dx =k \int\limits_a^b f(x)dx \\ \int\limits_a^b f(x)dx = - \int\limits_b^a f(x)dx \\ \int\limits_a^b f(x)dx + \int\limits_b^c f(x)dx = \int\limits_a^c f(x)dx \\ \int\limits_a^b (f(x)+g(x))dx= \int\limits_a^b f(x)dx + \int\limits_a^bg(x)dx$
Integrasjonskonstanten
Ettersom den deriverte av en konstant funksjon er lik null, må vi legge til en vilkårlig konstant til den integrerte av en funksjon.
- Eksempel: Integrasjonskonstant
- Vi tar for oss integralet
- <math>I=\int x\rm{d}x</math>
- Vi vet at <math>\frac{d}{dx}\frac12x^2=x</math>, men siden <math>\frac{d}{dx}C=0</math>, der <math>C</math> er en konstant, må vi legge denne til. Svaret blir altså
- <math>I=\int x\rm{d}x=\frac12x^2+C</math>
Merk at integrasjonskonstanten blir kansellert når <math>F(x)</math> brukes i sammenheng med det bestemte integralet. Det viser at verdien til <math>C</math> er vilkårlig.
3.1...Integrasjon ved variabelskifte
I derivasjon sier kjerneregelen at
<math>\frac{d}{dx}f(u)=\frac{du}{dx}\frac{d}{du}f(u)</math>
Dermed følger det at
<math>\int \frac{du}{dx}f(u(x))\rm{d}x=\int f(u)\rm{d}u</math>
Når vi substituerer variabler i integranden, manipulerer vi også differensialene <math>\rm{d}x</math> og <math>\rm{d}u</math>. Derfor skal vi nå vise hvordan man finner relasjonen mellom disse differensialene for en generell substitusjon. Deretter kan denne metoden anvendes på forskjellige integraler når de ikke kan løses direkte.
- Relasjoner mellom differensialer
- En generell substitusjon er
- <math>f(x)=g(u)</math>
- Vi vil finne relasjonen mellom differensialene <math>\rm{d}x</math> og <math>\rm{d}u</math> slik at vi kan foreta et variabelskifte.
- Dersom vi deriverer begge funksjonene mhp. x, får vi, ifølge kjerneregelen,
- <math>\frac{df(x)}{dx}=\frac{dg(u)}{du}\frac{du}{dx}</math>
- Vi ser dermed at relasjonen mellom differensialene er
- <math>\rm{d}x\frac{df(x)}{dx}=\rm{d}u\frac{dg(u)}{du}</math>
- eller
- <math>f^\prime (x)\rm{d}x=g^\prime (u) \rm{d}u</math>
Nå som vi kan manipulere differensialene, viser vi et eksempel der vi får bruk for dette:
- Eksempel 1: Variabelskifte
- Vi har integralet
- <math>I=\int \frac{\ln\,x}{2x}\rm{d}x</math>
- Vi observerer at <math>\frac{d}{dx}\ln\,x=\frac{1}{x}</math> og at begge disse er med i integranden. En god substitusjon her er derfor <math>\ln\,x=u</math>. Vi finner relasjonen mellom differensialene slik at vi kan gjennomføre variabelskiftet fra <math>x</math> til <math>u</math>.
- <math>\frac{d}{dx}\ln\,x=\frac{du}{dx}\,\Leftrightarrow\,\frac{1}{x}\rm{d}x=\rm{d}u\,\Leftrightarrow\,\rm{d}x=x\rm{d}u</math>
- Vi erstatter <math>\ln\,x</math> med <math>u</math> og <math>\rm{d}x</math> med <math>x\rm{d}u</math> i integranden. Da får vi
- <math>I=\int \frac{u}{2x}x\rm{d}u=\int\frac{1}{2}u\rm{d}u=\frac12\int u\rm{d}u=\frac14u^2+C</math>
- Vi substituerer tilbake fra <math>u</math> til <math>x</math> for å få svaret. <math>u=\ln\,x</math>, så
- <math>I=\frac14(\ln\, x)^2+C</math>
- Eksempel 2: Variabelskifte
- Vi har integralet
- <math>I=\int \tan\,x\rm{d}x</math>
- Vi vet at <math>\tan\,x=\frac{sin\,x}{\cos\,x}</math> og at <math>\frac{d}{dx}\sin\,x=\cos\,x</math>, si vi setter <math>u=\cos\,x</math>:
- <math>u=\cos\,x\,\Rightarrow\,\rm{d}u=-\sin\,x\rm{d}x</math>
- Vi setter inn i integralet og får
- <math>I=\int -\frac{1}{u}\rm{d}u=-\ln|u|+C</math>
- Vi kan nå erstatte u med x igjen får å få svaret vårt:
- <math>I=-\ln|cos\,x|+C</math>
- Eksempel 3: Variabelskifte
<math> \int 4e^{2x+1}dx \qquad \qquad \qquad\qquad \qquad setter \qquad u = 2x + 1 \\ \qquad \qquad \qquad \qquad \qquad \qquad\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad du = 2dx \\ \int 4e^{u}dx = \int 2e^{u}du = 2e^{u} + C = 2e^{2x+1} + C
</math>
- Eksempel 4: Variabelskifte
<math> \int \frac{1}{1+ \sqrt{x}}dx \qquad \qquad setter \qquad u = 1 + \sqrt{x}\\ \qquad \qquad \qquad \qquad \qquad \qquad\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \frac{du}{dx}= \frac12x^{- \frac12} \\ \qquad \qquad \qquad \qquad \qquad \qquad\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad du= \frac{1}{2 \sqrt{x}}dx \\ \qquad \qquad \qquad \qquad \qquad \qquad\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad dx= 2 \sqrt{x}du \\ \int \frac{1}{u}dx = \int \frac{1}{u}2 \sqrt{x}du
</math>
Man bruker at <math>u = 1 + \sqrt{x} </math> og får:
<math> \int \frac{1}{u}2 \sqrt{x}du = \int \frac{1}{u}2 (u-1)du = \int (2- \frac 2u)du = 2 \int du - 2\int \frac1u du = 2u -2ln|u| + k</math>
Substituerer tilbake til x og får:
<math> 2(1+ \sqrt x) -2ln(1 + \sqrt x) + k = 2 + 2\sqrt x - 2ln(1 + \sqrt x) + k = 2\sqrt x - 2ln(1 + \sqrt x)+ c </math>
Grenser ved variabelskifte
Når vi bruker variabelskifte og vi har et bestemt integral, vil grensene for integralet endres slik at integralet ennå gjelder for samme intervall. Dette vises best gjennom et eksempel:
- Eksempel: Endring av grenser ved variabelskifte
- La oss si at vi har integralet
- <math>I=\int_{0}^{\pi} \cos^2x\,\sin\,x\rm{d}x</math>
- Vi ser at <math>\frac{d}{dx}\cos\,x=-\sin{x}</math> og velger substitusjonen <math>u=\cos\,x</math>. Da får vi
- <math>\rm{d}u=-\sin\,x\rm{d}x\,\Rightarrow\,\frac{1}{-\sin\,x}\rm{du}</math>
- Grensene på integralet må vi endre slik at vi ennå integrerer over samme intervall. Vi gjør dette ved å sette inn grensene for x og løse med hensyn på u. Den nedre grensen blir
- <math>\cos\,0=u\,\Rightarrow\,u=1</math>
- Den øvre grensen blir
- <math>\cos\,\pi=u\,\Rightarrow\,u=-1</math>
- Vi setter alt inn i integralet og får
- <math>I=\int_1^{-1}u^2\frac{sin\,x}{-\sin\,x}\rm{u}\int_1^{-1}-u^2\rm{d}u=\left[-\frac13u^3\right]_1^{-1}=-\frac13(-1)^3-\left(-\frac13\cdot1^3\right)=2\cdot\frac13\cdot1^3=\frac23</math>
Delvis integrasjon
Vi kjenner allerede produktregelen fra dervasjon:
<math>\frac{d}{dx}uv=u\frac{d}{dx}v+v\frac{d}{dx}u</math>
Delvis integrasjon er produktregelen på integralform. Her skal vi utlede formelen for delvis integrasjon fra produktregelen:
- Utleding av delvis integrasjon fra produktregelen
- Vi starter med produktregelen
- <math>(uv)^\prime=u^\prime v+uv^\prime</math>
- og trekker fra <math>u\prime v</math> på hver side av likhetstegnet:
- <math>uv^\prime=(uv)^\prime-u^\prime v</math>
- Så integrerer vi:
- <math>\int uv^\prime \rm{d}x=\int (uv)^\prime-u^\prime v \rm{d}x=\int (uv)^\prime \rm{d}x-\int u^\prime v \rm{d}x=uv-\int u^\prime v \rm{d}x</math>
- <math>\int uv^\prime \rm{d}x=uv-\int u^\prime v \rm{d}x</math>
- Delvis integrasjon kan også skrives slik:
- <math>\int u\rm{d}v=uv-\int v\rm{d}u</math>
- ved at <math>\frac{dv}{dx}\rm{d}x=\rm{d}v</math> og <math>\frac{du}{dx}\rm{d}x=\rm{d}u</math>.
Dersom integralet består av forskjellige typer funksjoner (for eksempel en polynomfunksjon multiplisert med en trigonometrisk funksjon) kan delvis integrasjon være et godt førstevalg. Man bør velge u til en funksjon som blir "enklere" etter derivasjonen. Av og til må man utføre delvis integrasjon to ganger før man kommer til et resultat.
- Eksempel 1: integralet av naturlig logaritme
- Vi vil integrere funskjonen <math>f(x)=\ln\,x</math>. Til det kan vi bruke et lite triks og delvis integrasjon.
- Vi skriver <math>\ln\,x=1\cdot\ln\,x</math> og lar <math>u=\ln\,x</math> og <math>v=x</math>. Da får vi
- <math>\frac{du}{dx}=1</math> og <math>\frac{dv}{dx}=\frac1x</math>. Integralet blir
- <math>\int 1\cdot\ln\,x\rm{d}x=x\ln\,x-\int x\cdot\frac1x\rm{d}x=x\ln\,x-\int\rm{d}x=x\ln\,x-x+C</math>
- Resultatet er altså at
- <math>\int\ln\,x\rm{d}x=x\ln\,x-x+C</math>
- Svaret kan kontrolleres ved derivasjon.
- Eksempel 2:
<math>
\int(3x+2)sinx dx</math>
Setter u = 3x + 2 og v' = sin x
u' = 3 og v = - cos x
og får da:
<math>
\int(3x+2)sinx dx = (3x+2)\cdot (-cosx) - \int 3 \cdot (-cosx)dx = -(3x+2)cosx + 3 \int cosx dx \\ =-(3x+2)cosx + 3sinx + C </math>
- Eksempel 3:
Her kommer en litt spesiell variant.
<math> \int sin^2x dx = \int (sinx \cdot sinx) dx \\ = sinx \cdot (-cosx) - \int cosx \cdot (-cosx)dx \\
= - sinx cosx + \int (1-sin^2x) dx \\ = - sinx cosx + x - \int sin^2x dx</math>
Da har man:
<math> \int sin^2x dx = - sinx cosx + x - \int sin^2x dx \\ 2\int sin^2x dx = - sinx cosx + x \\ \int sin^2x dx = - \frac12 (sinx cosx - x) + C
</math>
- Eksempel 4:
Av og til må man integrere to ganger.
<math> \int x^2e^xdx </math>
setter <math>x^2 = u</math> og <math>e^x = v'</math>
da bli <math>u' = 2x</math> og <math> v=e^x</math>
da får man:
<math>\int x^2e^xdx = x^2 \cdot e^x - \int 2xe^xdx </math>
Så integrerer man en gang til og får:
<math>\int x^2e^xdx = x^2 \cdot e^x - (2xe^x -2\int e^xdx)= x^2 \cdot e^x - 2xe^x +2 e^x +C=(x^2-2x+2)e^x + C </math>