1T 2017 høst LØSNING: Forskjell mellom sideversjoner
| Linje 145: | Linje 145: | ||
Ja, den har en til. $f'(x)=3 $ gir også løsning for x = 3. Funksjonen har en parallell tangent i punktet (3, f(3)). | Ja, den har en til. $f'(x)=3 $ gir også løsning for x = 3. Funksjonen har en parallell tangent i punktet (3, f(3)). | ||
==Oppgave 13== | |||
===Oppgave 14=== | ===Oppgave 14=== | ||
Sideversjonen fra 17. des. 2017 kl. 16:27
Diskusjon av denne oppgaven på matteprat
Løsningforslag som video på UDL.no
Fullstendig løsningsforslag som pdf laget av Lektor Nilsen
Forslag til fasit (ikke løsningsforslag) laget av mattepratbruker Markus: del 1 del 2
Har du et alternativt løsningsforslag du ønsker å dele? Send inn til cosinus@matematikk.net så legger vi det ut!
DEL EN
Oppgave 1
$\frac{120 \cdot 25000}{0,15} =\frac{1,2 \cdot 10^2 \cdot 2,5 \cdot 10^4}{1,5 \cdot 10^{-1}} = 2,0 \cdot 10^{2+4-(-1)} = 2,0 \cdot 10^{7}$
Oppgave 2
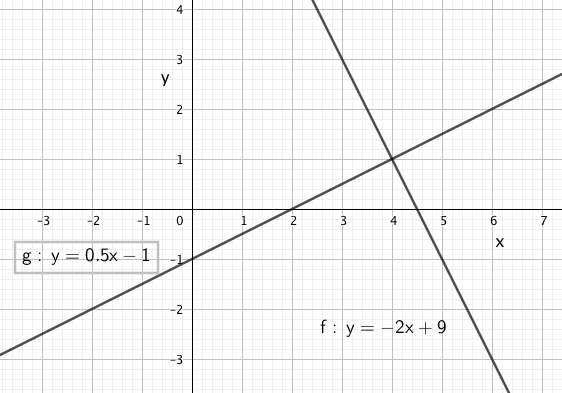
Fra figuren ser man at løsningen er x = 4 og y = 1.
Oppgave 3
$x^2-x- 12 \leq 0$
Faktoriserer (abc formel eller koeffisientmetode) og får:
$(x-4)(x+3) \leq 0$
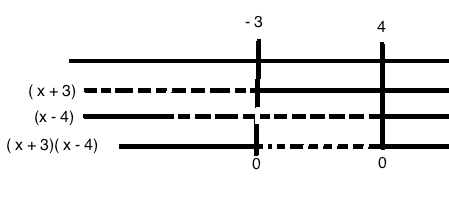
Tegner fortegnsskjema:
$x \in [-3, 4]$
Oppgave 4
$0< Sin (73^{\circ})< 1 \\ Tan(45^{\circ}) =1 \\ln 1 =0 \\ lg(10^{- \frac 14} = - \frac 14$
Rekkefølge blir da: $ lg(10^{- \frac 14}), \quad ln1, \quad Sin (73^{\circ}), \quad Tan(45^{\circ}) $
Oppgave 5
$lg(x + \frac{1}{25})= -2 \\ x + \frac{1}{25} = 10^{-2} \\ x= \frac{1}{100}- \frac{1}{25} \\ x= - \frac{3}{100} $
Oppgave 6
$\frac{\sqrt x +\sqrt x + \sqrt x}{\sqrt x \cdot \sqrt x \cdot \sqrt x} = \frac{3 \sqrt x}{x \sqrt x} = \frac{3}{x}$
Oppgave 7
$ \frac {\sqrt{75}}{\sqrt{30}} \cdot 5^{-1} \cdot 10^{\frac 12} + 8^{\frac 13} = \\ \frac {5 \sqrt{3}}{\sqrt{3} \sqrt{10}} \cdot \frac 15 \cdot \sqrt{10} + 2 = \\ 1+2 =3 $
Oppgave 8
Lineær funksjon: y= ax + b, stigningstallet er det samme i hele definisjonsområdet, altså $a = f'(x) = f'(2)= 3$
Vi har punktet (2, 4) og får:
$y = 3x + b \\ 4 = 3 \cdot 2 + b \\ b= -2$
som gir utrykket
f(x)= 3x -2
Oppgave 9
a)
$3x^2-9x = 3x(x - 3)$
b)
$\frac{x}{x-2} + \frac{2x}{x-3} - \frac{2x}{x^2-5x+6} \\ = \frac{x}{x-2} + \frac{2x}{x-3} - \frac{2x}{(x-3)(x-2)} \\= \frac{x(x-3)}{x-2} + \frac{2x(x-2)}{x-3} - \frac{2x}{(x-3)(x-2)} \\ = \frac{x^2-3x+2x^2-4x-2x}{(x-3)(x-2)} \\ = \frac{3x^2-9x}{(x-3)(x-2)} \\ = \frac{3x}{x-2}$
Oppgave 10
a)
A - Eleven går i 2A
$\bar{A}$ - Eleven går i 2B
B - Eleven har biologi
$\bar{B}$ - Eleven har ikke biologi
$P(B) = P(A) \cdot P(B|A) + P( \bar{A}) \cdot P(B| \bar{A}) = 0,5 + 0,25= 0,75$ altså 75%.
b)
$P(A|B) = \frac{P(A) \cdot P(B|A)}{P(A) \cdot P(B|A) + P( \bar{A}) \cdot P(B| \bar{A})} = \frac{0,5}{0,75} = \frac 23$
Det er to tredjedels sjanse for at tilfeldig elev med biologi går i 2A.
Oppgave 11
a)
$f(-1)= (-1)^4-2(-1)^3+2= 5 \\ f(1)= 1^4 - 2 \cdot 1^3 +2 = 1$
Endring i y verdi er -4 og endring i x verdi er 2. Gjennomsnittlig stigning blir da
$\frac{\Delta y}{\Delta x} = \frac{-4}{2} = -2$
b)
$f(x)= x^4-2x^3+2\\ f'(x)= 4x^3-6x^2 = 2x^2(2x-3)$
Den deriverte er null for x = 0 og f(0) = 2
$f'(-1)= -10 \\ f'(1)=-2 $
Funksjonen er strengt avtagende på begge sider av x=0. derfor er (0,2) et terassepunkt.
Oppgave 12
a)
$f(x)=x^3-6x^2+12x-8 \\ f'(x)= 3x^2-12x+12 $
b)
$y = ax + b \\ a = f'(1) = 3-12+12 =3 \\ f(1)= 3-6+12-8 =1 \\ y = ax + b \\ 1 = 3 +b \\ b= -2 \\ y=3 x-2$
c)
Ja, den har en til. $f'(x)=3 $ gir også løsning for x = 3. Funksjonen har en parallell tangent i punktet (3, f(3)).
Oppgave 13
Oppgave 14
a)
Radius i sirkelene er a.
Ser på figuren som to "delvise" sirkler og får at omkretsen blir:
$O= 2 \pi a + 2 \pi a = 4 \pi a$
b)
DEL TO
Oppgave 1
a)
b)
c)
d)
Oppgave 2
a)
b)
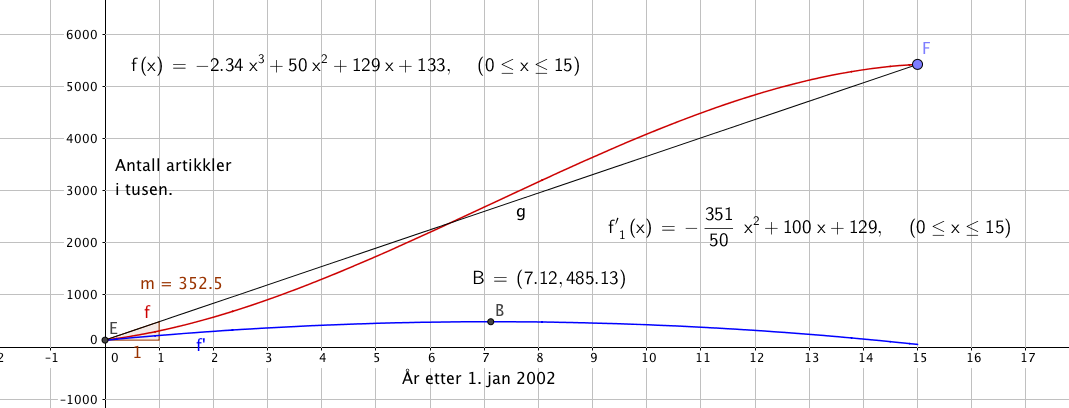
Oppgave 4
a)
b)
Oppgave 5
a)
Bunnpunkt eller minimumspunkt. Vi finner den deriverte og setter den lik null. X verdien setter vi inn i funksjonsuttrykket, så har vi punket.
$f(x) = 2x^2 - 7x +3 \\ f'(x)= 4x-7 \\ f'(x)=0 \\ 4x-7 = 0 \\ x= \frac 74$
$ f( \frac74) = 2 \cdot (\frac 74)^2 - 7 \cdot \frac 74 +3 = \frac{49-98+24}{8} = \frac{25}{8} $
Dersom man ønsker å trykke på knapper i stede for å tenke kan man jo gjøre den på CAS: