1P 2019 vår LØSNING: Forskjell mellom sideversjoner
| Linje 316: | Linje 316: | ||
===b)=== | ===b)=== | ||
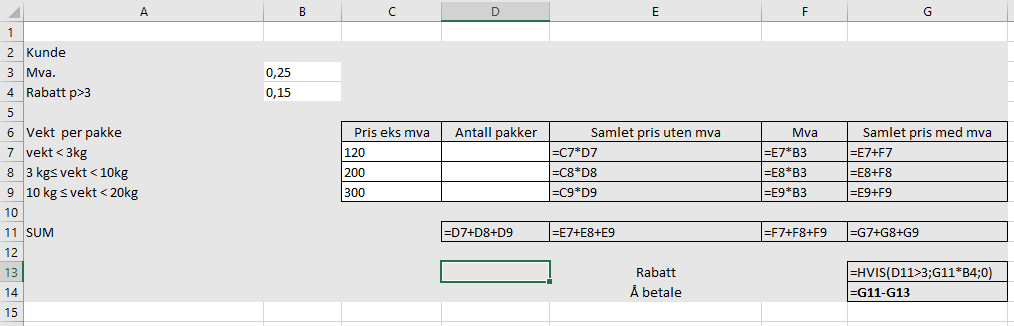
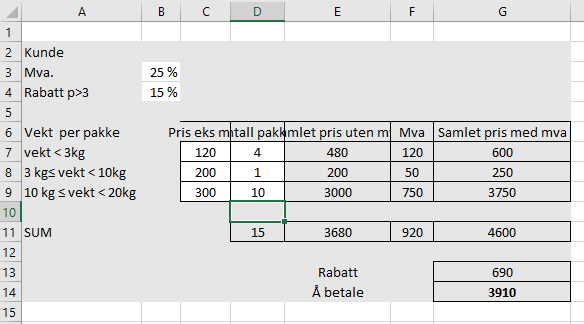
[[File:1p-v19-2-8-b.png]] | |||
===c)=== | ===c)=== | ||
Sideversjonen fra 26. sep. 2019 kl. 10:54
Diskusjon av oppgaven på matteprat
Løsningsforslag laget av Marius Nilsen ved Bergen Private Gymnas
DEL EN
Oppgave 1
a)
Bruker vekstfaktor.
$200 \cdot 1,15 = 230$
Det selges 230 biler i 2016.
b)
Antall biler gikk ned med 36. Nedgang i prosent:
$\frac{36}{240} \cdot 100 = 15$%
c)
Bruker vekstfaktor:
$x \cdot 0,8 = 200 \\ x= \frac{200}{0,8} \\ x = 250$
De solgte 250 biler i 2014.
Oppgave 2
$Reallønn = lønn \cdot \frac{100}{KPI} \\ KPI= \frac{lønn \cdot 100}{Reallønn}\\ KPI = \frac{550000 \cdot 100}{500000} \\KPI =110$
Oppgave 3
a)
Volum:
Finner arealet av grunnflaten ABF og multipliserer så med høyden BC:
$V = \frac{AB \cdot EF}{2} \cdot BC = \frac{16cm \cdot 6cm}{2} \cdot 12 cm= 576cm^3$
b)
Overflate:
Ett stort rektangel ABCD: $AB \cdot BC = 16cm \cdot 12 cm = 192 cm^2$
To like store trekanter ABF og DCG: $AB \cdot EF = 16cm \cdot 6 cm = 96 cm^2$ (totallene går mot hverandre)
Bruker Pytagoras for å finne AF som blir 10 cm. De to små rektanglene AFGD og BFGC blir da $2 \cdot 10cm \cdot 12 cm = 240cm^3$
Når vi legger sammen disse tre arealene, tilsammen fem sider, får vi overflaten av klossen:
$96cm^2 + 192cm^2+ 240cm^2 =528cm^2$
Oppgave 4
Når blandingsforholdet er 2:5 har vi totalt 7 deler som i dette tilfelle skal utgjøre 10,5 liter blanding. For å finne ut hvor stor en del er tar man 10,5 liter : 7 = 1,5 liter. Vi trenger altså 3 liter rengjøringsmiddel (to deler) og 7,5 liter vann.
Oppgave 5
a)
b)
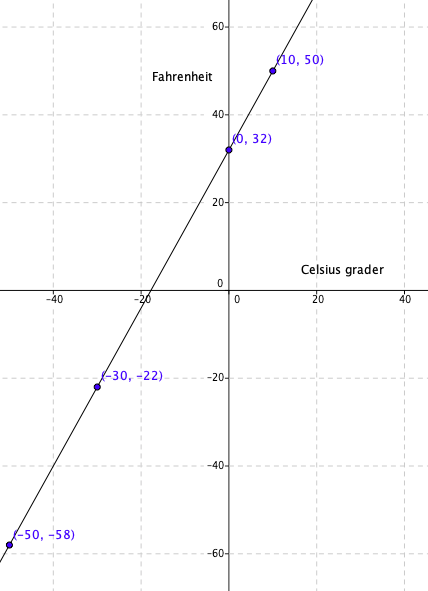
Størrelsene er ikke proporsjonale. Grafen til to proporsjonale størrelser er en rett linje gjennom origo.
c)
Fra figuren i a ser man at når det er $-40^{\circ}C$ er det også - 40 Fahrenheit. Begge gradestokkene vil da vise samme tallverdi.
d)
En rett linje er gitt som y= ax + b
I dette tilfelle er x = C og y = F, b = 32
Vi får da: F = aC + 32
For å finne stigningstallet, a, bruker vi de to siste punktene gitt i oppgaven ( 0, 32) og (10, 50). Man kan bruke hvile to punkter man vil men det lønner seg alltid å velge verdier som gir enklest mulig regning. Vi tar endring i y verdi delt på endring i x verdi:
$a = \frac{\Delta y}{\Delta x} = \frac{50 - 32}{10-0}= \frac{18}{10} = \frac 95$ som er stigningstallet. Sammenhengen blir da:
$F = \frac 95 C + 32$
e)
$ F(C) = \frac 95 C + 32 \\F(100) = \frac 95 \cdot 100 + 32 \\ F(100) = \frac{9 \cdot 100}{5} + 32 \\ F(100)= 9 \cdot 20 +32 = 212$
Altså er $100^{\circ} C = 212^{\circ}F$
Oppgave 6
a)
Hendelse M: I rute mandag - 80% Hendelse F: I rute fredag - 90%
Dersom begge henvendelsene skal inntreffe bruker vi multiplikasjonssetningen for å finne sannsynligheten:
P (M og F) = $P(M) \cdot P(F) = \frac{80}{100} \cdot \frac{90}{100} = \frac{7200}{10000}= \frac {72}{100} = 72$ %.
Det er 72% sannsynlig at toget er i rute begge dagene.
b)
Dersom toget skal være i rute kun en av dagene kan det skje på to måter:
1: Toget er i rute mandag, men ikke fredag
2: Toget er i rute fredag, men ikke mandag.
P( i rute kun EN dag) = $P(M)\cdot P( \bar{F}) + P(F) \cdot P(\bar{M})$
Streken over F og M betyr sannsynligheten for at det IKKE er i rute M (mandag) eller F (fredag).
Vi får: P( i rute kun EN dag) = $0,8 \cdot 0,1 + 0,9 \cdot 0,2 = 0,26$ som er 26%.
Oppgave 7
a)
Dersom åtte personer skal dele en kostnad på 18 000 kroner blir det 18000 : 8 = 2250
Hver person må betale kr. 2250,-
b)
Dette er omvendt proporsjonale størrelser, det blir billigere for den enkelte jo flere som er med, men prisen for den enkelte synker mest med de første som blir med.
$U(x)= \frac{18000}{x}$
c)
I den første grafen avtar det jevnt, med en fast verdi for en økning av x. Slik er det ikke i vårt tilfelle der det avtar mest i starten, altså er grafen til høyre en riktig beskrivelse av utviklingen.
DEL TO
Oppgave 1
a)
b)
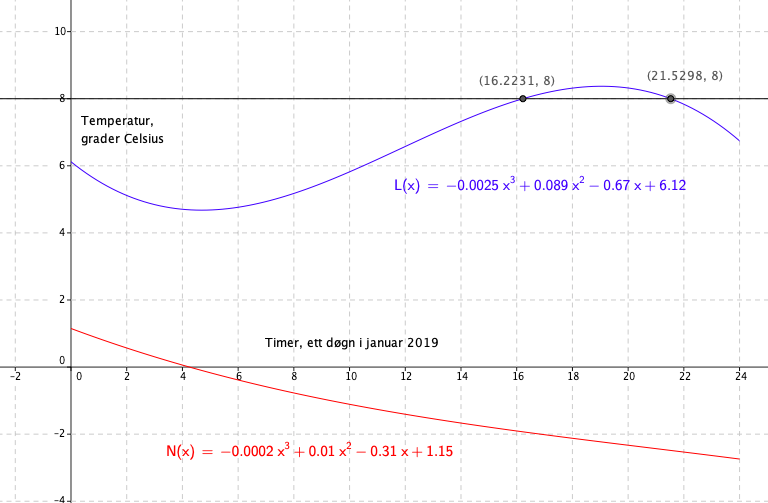
Fra a ser vi at temperaturen på Lindesnes var over 8 grader , fra litt etter fire til mellom ni og ti på kvelden. For å få det nøyaktig på minuttet må vi huske at Geogebra jobber med tideler og hundredeler, mens minutter er sekstideler. Vi tar desimalene og konverterer til minutter:
, 223 : $\frac{22}{100} = \frac{x}{60} \\ x = 13$
og
,53: $\frac {53}{100} = \frac{x}{60} \\ x = 32 $
Temperaturen var over åtte grader fra 16: 13 til 21: 32.
c)
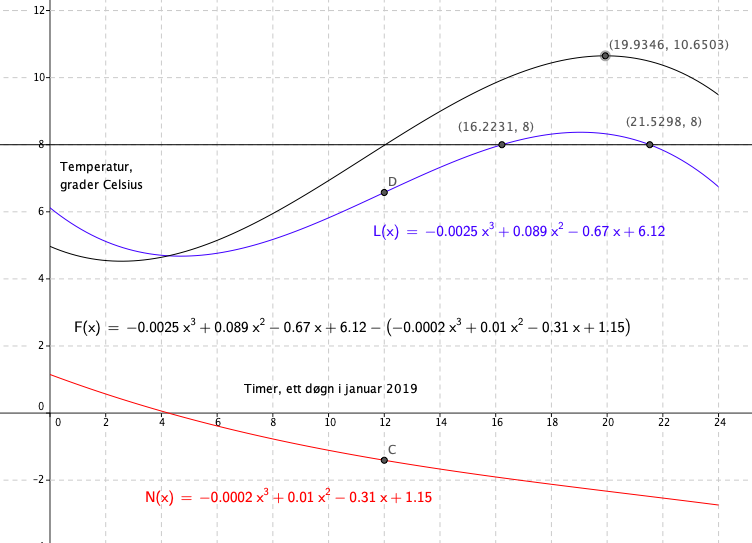
Temperaturforskjell kl 12:00
$L(12) - N(12) =6,6 - (- 1,4) = 8$ grader.
d)
e)
Funksjonen F viser temperaturforskjellen mellom de to stedene. Den var størst ca kl 8 på kvelden, og var da ca 10, 7 grader. Altså var det 10,7 grader varmere på Lindesnes enn på Nordkapp kl 8 på kvelden.
Oppgave 2
a)
Setter tallene rett inn i formelen, fordi de spør etter V:
$ V = 4 \cdot m \cdot A \\ V = 4 \cdot 63 \cdot 25 \\ V =6300$ ml,
som er 6,3 liter.
b)
Her spør man om A, derfor løser vi først formelen med hensyn på A ( får A alene på venstre side), så setter vi inn tall:
$V = 4 \cdot m \cdot A \\ A = \frac {V}{4m} \\ A = \frac{10000}{4 \cdot 85} = 29,4$
Pasienten har forbrent ca 30 % av kroppens overflate. (Husk at volumet som skal inn i formelen er i milliliter, altså 10 000, ikke 10.
Oppgave 3
a)
Volumet av en sylinder er grunnflate gange høyde. Grunnflaten er en sirkel med radius 13cm. Vi får:
$ V = \pi r^2 \cdot h = \pi \cdot (13cm)^2 \cdot 8 cm = 4247 cm^3 = 4,25 dl^3 = 4,25$ liter.
b)
Diameter marsipanlokk: 26 cm + 16 cm + 7 cm = 49 cm
Radius blir 24,5 cm
Areal marsipanlokk $A = \pi r^2 = \pi \cdot (24,5cm) ^2 = 1886 cm^2 $
c)
Omkrets kake: $O = 2 \pi r = 2 \pi \cdot 13 cm = 82cm$
Overflateareal kake: $ O = 2\pi \cdot r \cdot h + \pi r^2 = 2 \cdot \pi \cdot 13 cm \cdot 8cm + \pi \cdot (13cm^2= 1184 cm^2$
Forhold mellom areal til marsipanlokk og overflateareal til kake er $\frac{1886 cm^2}{1184cm^2} = 1,59 \approx 1,6$
Oppgave 4
a)
Krysstabell:
| under tredve | over tredve | Sum | |
| kildesorterer | $ 0,14 \cdot 250 = 35$ | $ 0,44 \cdot 750 = 330$ | 365 |
| kildesorterer ikke | $0,86 \cdot 250 = 215$ | $0,56 \cdot 750 = 420$ | 635 |
| Sum | 250 | 750 | 1000 |
b
$ \frac{365}{1000} = 0,365 = 36,5$ %
c)
$ \frac {35}{365} =0,096 = 9,6$ %
Oppgave 5
a)
Skatt:
$(76450kr - 54650kr) \cdot 0,25 = 5450 kr.$
b)
20% av 25000 kr er 5000kr. Trekker man det fra svaret i a får man at hun kun betaler 450 kr i skatt.
Oppgave 6
a)
Vinkel ABE og CDE er samsvarende fordi linjestykkene AB og DC er parallelle. Det samme gjelder vinkel EAB og ECD. I E har vi toppvinkler. Vinklene i de to trekantene er parvis like store, derfor har vi formlikhet.
b)
Lengdeforholdet i trekantene er: $\frac{AB}{DC} = \frac{18}{4} = \frac 31$
Forholdet 3 :1 gir fire deler, hvorav lengden av DE er en fjerdedel av DE, altså $18 \cdot \frac{1}{4} = 4,5$
DE = 4,5
Oppgave 7
Jeg velger å finne avstanden i kilometer først, så gjør jeg antall kilometer om til nautiske mil (nm).
$\frac{1}{50000} = \frac{53}{x} \\ x= 53 \cdot 50000 = 2650000$
Siden vi satte inn 53 cm i likningen er svaret vårt i cm. 2650000 cm = 26500m
Vi tar så antall meter vi fikk og deler på 1852m for å finne antallet nautiske mil: $\frac{26599}{1852} = 14, 3$ nm.