2P 2019 vår LØSNING: Forskjell mellom sideversjoner
| Linje 147: | Linje 147: | ||
[[File:2p-v19-2-4-a.png]] | [[File:2p-v19-2-4-a.png]] | ||
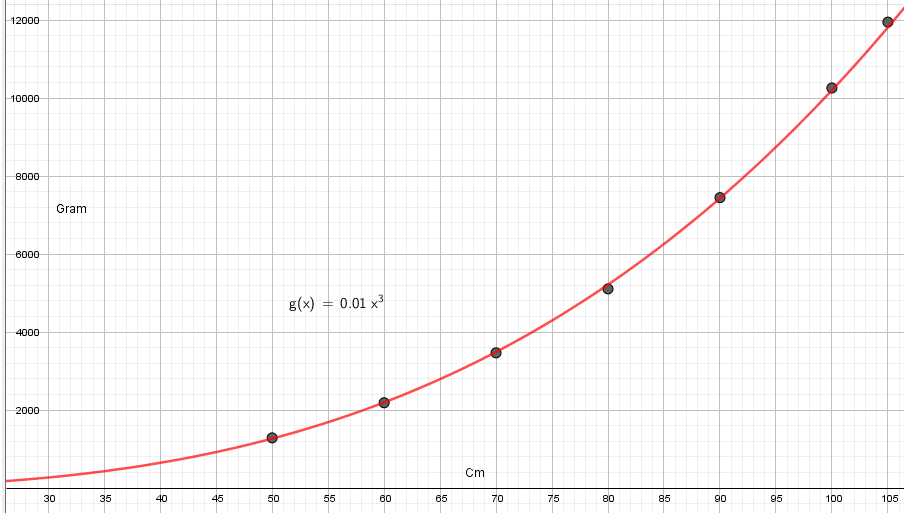
Bruker regresjon i Geogebra. a = 0,01 og b = 3. | |||
===b)=== | ===b)=== | ||
Sideversjonen fra 27. sep. 2019 kl. 09:02
Løsningsforslag laget av Marius Nilsen ved Bergen Private Gymnas
DEL EN
Oppgave 1
Organiserer datamaterialet i stigende rekkefølge:
0,0, 1,1,1,1, 2,2,2,2,2, 3,3,3, 4, 5,5, 6, 8, 9
Variasjonsbredden er største minus minste verdi: 9 - 0 = 9
Median er gjennomsnittet av de to tallene i midten (fordi antall verdier er partall): 2
Gjennomsnittet er summen delt på antall observasjoner: $\frac{60}{20} = 3$
Oppgave 2
$0,8x = 640 \\ x = \frac{640}{0,8} \\ x = 800$
Varen kostet 800 kroner.
Oppgave 3
$7,03 \cdot 10^7 - 7000000 = \\ 7,03 \cdot 10^7 - 0,7 \cdot 10^7 = \\ (7,03- 0,7) \cdot 10^7 = \\ 6,33 \cdot 10^7$
Oppgave 4
$\frac{2^0+2^3 \cdot 2^2 + (2^3)^2 - 2}{2 \cdot 2^2} +2^{-3} = \\ \frac{1+8\cdot 4+ 64-2}{8} + \frac 18 = \\ \frac{95}{8} + \frac 18 = \\ \frac{96}{8} = 12$
Oppgave 5
a)
y = ax + b, der a er stigningstall og b er skjæring med y akse (konstantledd). Vi ser at grafen øker med 200 når antallet pakker øker fra 4 til 8. Det betyr at a = 50.
Vi har at:
$350 = 50 \cdot 4 + b \\ b = 150 $
Altså y = 50x + 150
b)
Det koster 50 kroner per pakke (stigningstall a). x er antall pakker. Det koster 150 kroner for å få budfirmaet til å møte opp (konstantledd b), altså en fast kostnad.
Oppgave 6
a)
Når man skal regne gjennomsnitt i klassedelt materiale antar vi at gjennomsnittet i hver klasse ligger på klassemidpunktet, selv om vi egentlig ikke vet noe om det. Det viser seg at dette ofte blir ganske riktig.
Klaaemidpunktene er: 5, 15, 30 og 60.
Vi multipliserer disse med den tilhørende frekvensen, legger sammen resultatene for alle klassene ( her er det fire) og deler på det totale antall (200):
$Gjsnitt = \frac{5 \cdot 60 + 15 \cdot 80 + 30 \cdot 50 + 60 \cdot 10}{200} = \frac{300 + 1200 + 1500 + 600}{200} = \frac{3600}{200} = 18$
Gjennomsnittlig reisetid er ca. 18 minutter.
b)
Når det er 200 elever, er medianeleven gjennomsnittet av elev 100 og 101, altså cirka 40 elever inn i klasse [10, 20>. Dette er midt i klassen, siden den har 80 elementer. I Stigende rekkefølge, jevnt fordelt, blir medianverdien ca 15 minutter, som også er klassemidtpunkt.
c)
Oppgave 7
a)
b)
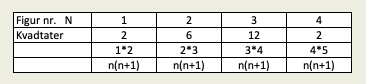
Ved å bruke de små kvadratene til å lage ett stort ser man at man hele tiden får ett lite kvadrat til overs, altså $n^2 + 1$
c)
Antall kvadrater i figur nr. n kan uttrykkes som $A(n) = n^2 + n$.
DEL TO
Oppgave 1
a)
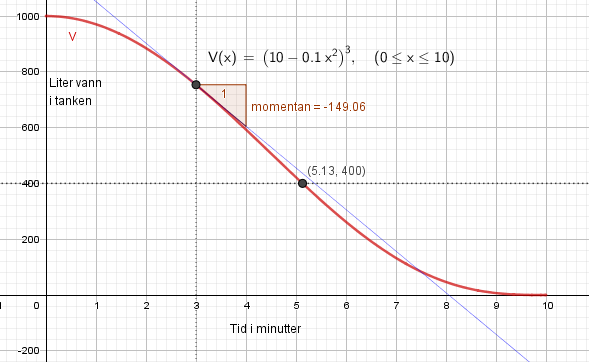
$V(x)= (10-0,1x^2)^3 \quad 0\leq x \leq 10$
$V(0) = 10^3 = 1000$
Tanken rommer 1000 liter.
b)
c)
Fra figuren i b ser man at det tar 5,13 minutter i desimal tid. Vi gjør 0,13 om til sekunder:
$\frac{13}{100} =\frac {x}{60} \\ x =7,8$
Det tar 5 minutter og 8 sekunder før det er 400 liter igjen i tanken.
d)
1000 liter tømmes på 10 minutter. Det blir i gjennomsnitt 1000 liter/ 10 min som er 100 L/min.
e)
Se figuren i b: Lag linjen x=3 og finn skjæring med grafen. I punktet lager man tangenten til grafen. Stigningen til tangenten i punktet er den momentane veksten for x =3. Den er - 149. Det betyr at akkurat når det har gått 3 minutter tømmes tanken med en fart på 149 L/ min.
Oppgave 2
Oppgave 3
a)
5,3 millioner = 5 300 000 = $ 5,3 \cdot 10^6$
Dette er en litt uklar oppgave, men her antar man at det er plasten i en vegg som er 0,035mm, da blir tykkelsen av en pose 0,070 mm.
180 poser med en høyde på 0,07 mm = 0,00007 meter = $7,0 \cdot 10^{-5}$
Høyde: $h =7,0 \cdot 10^{-5} \cdot 5,3 \cdot 10^6 \cdot 180 m = 66780$ meter.
b)
Oppgave 4
a)
Bruker regresjon i Geogebra. a = 0,01 og b = 3.
b)
Oppgave 5
a)
b)
Oppgave 6
Oppgave 7
Situasjon 1:
Dette er en lineær sammenheng. 9 kroner er konstantleddet, og stigningstallet er 15 kroner. x er antall hektogram. Kurve H beskriver situasjonen.
Situasjon 2
Når en størrelse vokser med en fast prosent, vil det si at den vokser eksponentielt. Graf B beskriver forløpet.
Situasjon 3
Et eksempel på at det lønner seg å følge med i naturfagtimene også :-) Når noe først vokser tilnærmet eksponentielt, for så å stabilisere seg har man det man i naturfag kaller sigmoid vekst som beskrives med en såkalt S kurve. I matematikken kalles dette for logistisk modell. Den kurven som passer best er graf F.
Situasjon 4
Vi tenker på prisen det koster å sende pakke som y verdien. Vi ser at det kun er tre forskjellige verdier som ikke er kontinuerlige. Hver av prisene gjelder innen et vekt intervall. Graf C passer.