2P 2019 høst LØSNING

Oppgaven som pdf

Diskusjon av oppgaven på matteprat

Løsning del 2 laget av mattepratbruker Kristian Saug

Oppgave 1

1, 1, 2, 2, 2, 3, 3, 3, 3, 3, 4, 4, 4, 4, 5, 5, 5, 6, 6, 8

a)

Median er gjennomsnittet av de to tallene i midten av tallmaterialet ( tall 10 og 11) som er $\frac{3+4}{2}=3,5$

Gjennomsnittet er summen av alle observasjoner, delt på antallet observasjoner, altså:

$\frac{1+1+2+2+2+3+3+3+3+3+4+4+4+4+5+5+5+6+6+8}{20}=\frac{66}{20}=3,3$

Oppgave 2

Dersom 15 stk er hvite og 40% er røde, vet vi at 60% tilsvarer 15 stk. Da er 20% lik 5 stk. 40% er da 10 stk.

$\frac{15\cdot 40}{60}=10$

Vi deler 15 på 60 som gir en prosent, multipliserer med 40 for å finne hvor mange 40% er. Det er altså 10 stk.

Oppgave 3

$$\begin{gathered} \frac{1,2\cdot {10}^7-6,5\cdot {10}^6}{0,0005}= \\ \frac{(12-6,5){10}^6}{5\cdot {10}^{-4}}= \\ \frac{5,5}{5}\cdot {10}^{6-(-4)}= \\ 1,1\cdot {10}^{10} \end{gathered}$$

Eller slik:

$$\begin{gathered} \frac{1,2\cdot {10}^7-6,5\cdot {10}^6}{0,0005}= \\ \frac{12000000-6500000}{5\cdot {10}^{-4}}= \\ \frac{5500000}{5}\cdot {10}^4= \\ 1100000\cdot {10}^4=1,1\cdot {10}^{10} \end{gathered}$$

Oppgave 4

Vi omformer tallene slik at det blir lettere å sammenligne dem:

$$\begin{gathered} {75}^0=1 \\ {2}^3\cdot 2^2=32 \\ (2^3{)}^2=64 \\ {2}^{-3}=\frac{1}{8} \\ \frac{1}{4^2}=\frac{1}{16} \end{gathered}$$

Vi får da følgende rekkefølge :

$\frac{1}{4^2},2^{-3},{75}^0,2^3\cdot 2^2,(2^3{)}^2$

Oppgave 7

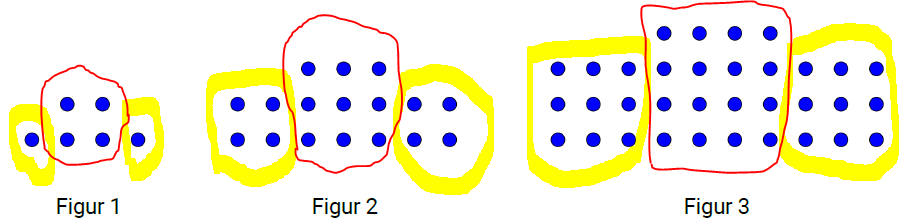
Vi legger merke til at alle figurene kan deles i tre. De to gule delene er like. I figur 2 er antallet sirkler $2^2$ i en gul del, og $3^2$ i figur 3.

a)

Fra figuren over ser man at figur nr. 4 vil bestå av fire ganger fire, pluss fem ganger fem, pluss fire ganger fire antall kuler:

$4^2+5^2+4^2=16+25+16=57$

Det er 57 kuler i figur 4.

b)

Vi ser at de to "gule" kvadratene har sidekanter med samme antall kuler som figurnummer, mens det "røde" kvadratet i midten har en kule mer i sidekanten enn figurnummeret.

Kaller antall kuler for A(n)

Vi får da:

$A(n)=n^2+(n+1{)}^2+n^2=2n^2+(n+1{)}^2=2n^2+n^2+2n+1=3n^2+2n+1$

c)

Figur nr. 100:

$A(100)=3\cdot {100}^2+2\cdot 100+1=30000+200+1=30201$