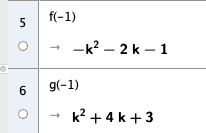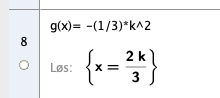1T 2019 høst LØSNING

Oppgaven som pdf

Diskusjon av denne oppgaven på matteprat

Løsningsforslag del 1 laget av mattepratbruker Emilga

Løsningsforslag del 2 laget av mattepratbruker Kristian Saug

DEL EN

Oppgave 1

$\frac{0,00046\cdot 25000000}{0,05}=\frac{4,6\cdot {10}^{-4}\cdot 25\cdot {10}^6}{5\cdot {10}^{-2}}=4,6\cdot 5\cdot {10}^{-4+6+2}=23\cdot {10}^4=2,3\cdot {10}^5$

Oppgave 2

$\left[\begin{array}{r}2x+3y=6\\ 5x+6y=18\end{array}\right]$

Velger å bruke addisjonsmetoden. Multipliserer første likning med -2:

$\left[\begin{array}{r}-4x-6y=-12\\ 5x+6y=18\end{array}\right]$

Legger likningene sammen og får:

x = 6

Setter x = 6 inn i første likning og får y = - 2

Løsning: ( 6, -2)

Oppgave 3

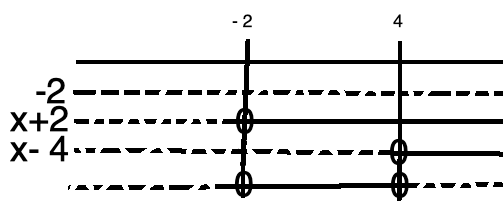
-2 (x+2)( x - 4) > 0

Uttrykket i ulikheten er ferdig faktorisert, så man kan sette opp et fortegnsskjema med en gang og finne ut når uttrykket på venstre side er større enn null.

$x\in <-2,4>$

Oppgave 4

$\frac{2x^2+x+3}{x^2-9}-\frac{x}{x+3}=\frac{2x^2+x+3-x(x-3)}{(x+3)(x-3)}=\frac{x^2+4x+3}{(x+3)(x-3)}=\frac{(x+3)(x+1)}{(x+3)(x-3)}=\frac{x+1}{x-3}$

a)

$$\begin{gathered} lg(4x)=0 \\ {10}^{lg(4x)}={10}^0 \\ 4x=1 \\ x=\frac{1}{4} \end{gathered}$$

b)

$$\begin{gathered} lg(\frac{\sqrt{50}}{x})=\frac{1}{2} \\ {10}^{lg(\frac{\sqrt{50}}{x})}={10}^{\frac{1}{2}} \\ \sqrt{50}=x\sqrt{10} \\ x=\frac{\sqrt{50}}{\sqrt{10}}=\sqrt{\frac{50}{10}} \\ x=\sqrt{5} \end{gathered}$$

c)

$$\begin{gathered} 2^{x^2}\cdot 2^{3x}=16 \\ {2}^{x^2+3x}=2^4 \\ {x}^2+3x-4=0 \\ x=-4\vee x=1 \end{gathered}$$

Oppgave 6

Den rette linjen som går gjennom ( -7, -1) og (5, 2):

En rett linje kan skrives som y = ax + b

Finner stigningstallet a:

$a=\frac{\mathrm{\Delta }y}{\mathrm{\Delta }x}=\frac{2-(-1)}{5-(-7)}=\frac{2+1}{5+7}=\frac{1}{4}$

Du kan nå bruke ettpunktsformelen, eller tenke:

$$\begin{gathered} y=ax+b \\ 2=\frac{1}{4}\cdot 5+b \\ b=\frac{3}{4} \end{gathered}$$

Likningen for linjen er da:

$y=\frac{1}{4}x+\frac{3}{4}$

Oppgave 7

$$\begin{gathered} a{x}^2+3x+1=x-2x\ne 0 \\ a{x}^2+2x+3=0 \end{gathered}$$

Fra abc- formelen vet vi at en løsning oppstår dersom $b^2-4ac=0$ :

$$\begin{gathered} 2^2-4\cdot a\cdot 3=0 \\ 4-12a=0 \\ a=\frac{1}{3} \end{gathered}$$

a lik en tredjedel gir en løsning.

Oppgave 8

a)

$$\begin{gathered} f(x)=x^3+4x^2+x-6 \\ {f}^{\prime }(x)=3x^2+8x+1 \end{gathered}$$

b)

Momentan vekstfart i (-3, f(-3)):

$f^{\prime }(-3)=3\cdot (-3{)}^2+8\cdot (-3)+1=27-24+1=4$

c)

Gjennomsnittlig vekstfart [ -1, 2 ]:

$$\begin{gathered} f(-1)=(-1{)}^3+4(-1{)}^2+(-1)-6=-1+4-1-6=-4 \\ f(2)=2^3+4\cdot 2^2+2-6=8+16+2-6=20 \\ \frac{f(2)-f(-1)}{3}=\frac{20-(-4)}{3}=8 \end{gathered}$$

Den gjennomsnittlige vekstfarten i intervallet er 8.

a)

b)

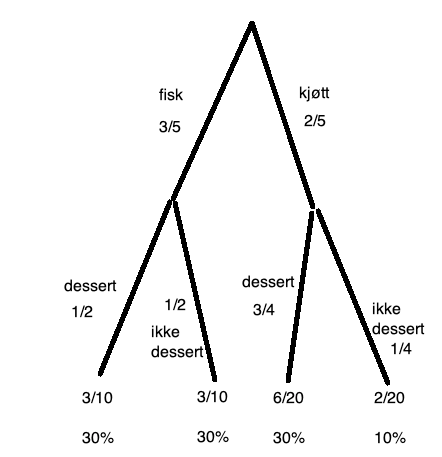
Fra valgtre:

$P(des)=\frac{3}{5}\cdot \frac{1}{2}+\frac{2}{5}\cdot \frac{3}{4}=\frac{3}{10}+\frac{6}{20}=\frac{6}{10}$

60% ønsket dessert.

Oppgave 10

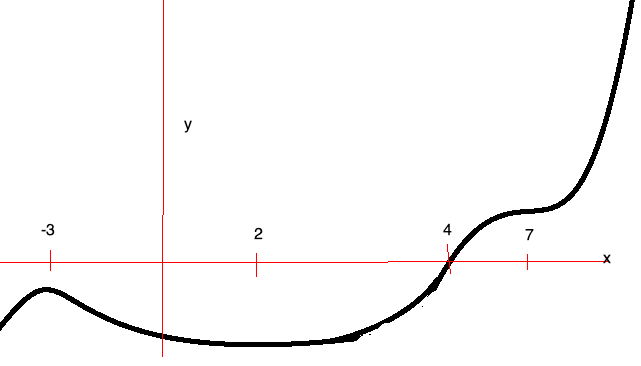
x= -3: Funksjonen har et toppunkt, men har negativ verdi.

x= 2: Funksjonsverdi fortsatt negativ og funksjonen har et bunnpunkt.

x= 4: Funksjonen vokser (deriverte positiv). Den har et nullpunkt

x= 7: Funksjonen har et terrassepunkt. Den deriverte har et nullpunkt, men samme fortegn (positiv) på begge sider av nullpunktet.

a)

Bruker pytagoras:

$$\begin{gathered} x^2+x^2=(4\sqrt{2}{)}^2 \\ 2x^2=32 \\ {x}^2=14 \\ x=4 \end{gathered}$$

b)

$\tan (v)=\frac{motståendekat}{hosliggendekat}=\frac{4}{4}=1$

c)

$\sin (v)=\frac{motståendekatet}{hypotenus}=\frac{4}{4\sqrt{2}}=\frac{1}{\sqrt{2}}=\frac{\sqrt{2}}{\sqrt{2}\cdot \sqrt{2}}=\frac{\sqrt{2}}{2}$

Oppgave 12

Vi bruker arealsetningen:

$A=abSinC=3\sqrt{2}\cdot 8\cdot \frac{\sqrt{2}}{2}=3\cdot 2\cdot 4=24$

Nå var sinus til vinkelen oppgitt i forrige oppgave. Dersom du ikke husker den kan du utlede den ved å tegne en rettvinklet trekant med hypotenus 1.

a)

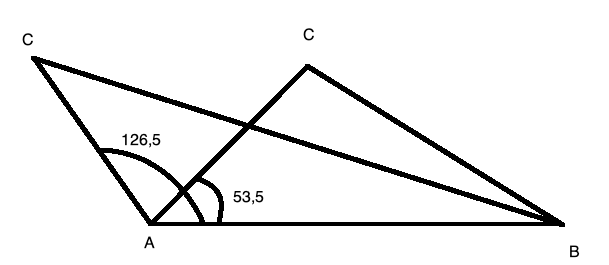
I området 0 - 180 grader har en sinusverdi to løsninger (sjekk enhetssirkelen).

Vi har symmetri, så dersom en vinkel er $53,5^{\circ }$ så er den andre ${180}^{\circ }-53,5^{\circ }=126,5^{\circ }$

b)

Oppgave 1

a)

b)

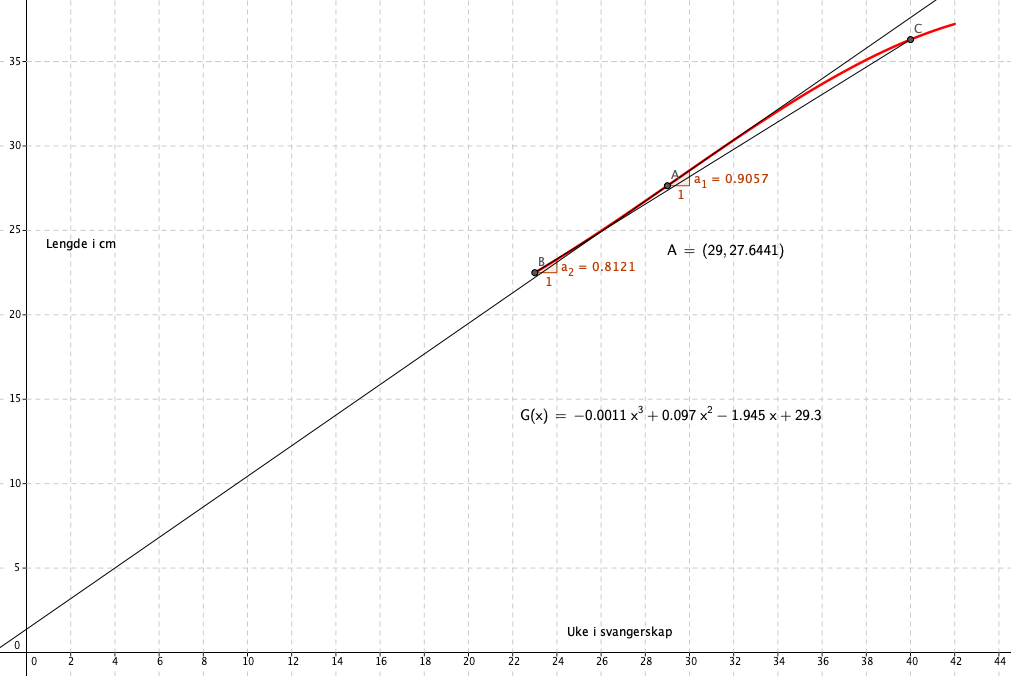
I uke 29 er den momentane vekstfarten 0,9 cm. Det betyr at avstanden øker 0,9 cm i uke 29.

c)

Økningen i denne perioden er i gjennomsnitt ca 8 mm per uke. Se figur i a.

Oppgave 2

a)

	Tysk	ikke Tysk	Sum
1T	$6$	$8$	14
ikke 1T	$6$	$10$	16
Sum	12	18	30

b)

P (tysk, men ikke 1T) = $\frac{6}{30}=\frac{1}{5}$

c)

P( tysk, gitt ikke 1T) = $\frac{6}{16}=\frac{3}{8}$

Oppgave 3

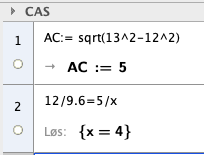
Regner i CAS:

Finner BC ved pytagoras, har formlikhet i de to trekanten og finner så DE = 4.

Oppgave 5

a)

Nullpunkter: x = 0 eller x = k ( linje 3)

b)

Linje 4 i a:

$f^{\prime }(x)=3x^2-4kx+k^2$

c)

Både figur A og C stemmer med nullpunkter og ekstremalpunktets x verdi. Vi sjekker funksjonen og den deriverte for x = -1:

Vi ser at funksjonsverdien er negativ og den deriverte positiv, altså er det figur C som viser grafen til f.

d)

Bruker linje (punkt)(punkt) kommando i CAS og får:

Stigningstall: $-\frac{2k^2}{9}$

e)

Setter den deriverte lik $-\frac{k^2}{3}$ og får bare ett svar som tilfredsstiller likningen,

$x=\frac{2k}{3}$.

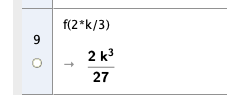
Finner y koordinaten til punktet ved å sette resultatet over inn i f:

Tangeringspunkt : $(\frac{2k}{3},\frac{2k^3}{27})$