S1 2019 høst LØSNING: Forskjell mellom sideversjoner
| Linje 129: | Linje 129: | ||
$495-330=165$ | $495-330=165$ | ||
==Oppgave 7)== | |||
Opplysningene gir oss følgende likningssett, hvor x er prisen for skolegang for ett barn i én måned, og y er prisen for barnehjemsplass for ett barn i én måned. | |||
<math> \left[ \begin{align*} 2x+y=700 \\ 4x+3y=1700 \end{align*}\right] </math> | |||
Uttrykker likning I ved y: | |||
$y=700-2x$ | |||
Setter inn verdien av y i likning II: | |||
$4x+3(700-2x)=1700 \\ 4x+2100-6x=1700 \\ -2x = -400 \\ x=200$ | |||
Fra likning I: | |||
$y=700-2\cdot 200=700-400=300$ | |||
Per barn per måned koster det 200kr for skolegang og 300kr for barnehjemsplass. For 20 barn blir det totalt: | |||
$20\cdot 200kr + 20\cdot 300kr=4000+6000=10000$ | |||
Klassen til Kari må samle inn 10 000 kr hver måned. | |||
Sideversjonen fra 28. des. 2019 kl. 14:06
Diskusjon av denne oppgaven på matteprat
Løsningsforslag laget av Svein Arneson
Løsningsforslag del 1 laget av Emilga
Løsningsforslag del 2 laget av Kristian Saug
DEL 1
Oppgave 1)
a)
$x^2+4x-12=0 \\ (x-2)(x+6)=0 \\ x=-6 \vee x=2$
b)
$lg(5-2x)=1 \\ 5-2x =10 \\ -2x = 5 \\ x= -\frac{5}{2}$
Oppgave 2)
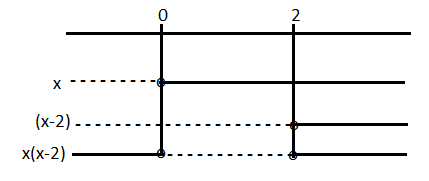
$x^2-2x<0$
Finner nullpunktene.
$x(x-2)=0 \\ x=0 \vee x=2$
$x^2-2x<0$ når $0<x<2$
Oppgave 3)
$x^2+4y=4x \\ 4x-2y=6$
Ganger likning II med 2 og bruker addisjonsmetoden.
Likning II ganger 2:
$8x-4y=12$
Legger sammen likningene:
$x^2+4y+8x-4y=4x+12 \\ x^2+4x-12=0 \\ x_1=-6 \vee x_2=2$
(Samme likning som i oppgave 1a)
Gjør om likning II:
$4x-2y=6 \\ -2y=6-4x \\ y=-3+2x$
Setter inn de to x-verdiene:
$y_1=-3 + 2\cdot (-6) = -15$
$y_2=-3+2\cdot 2=1$
Løsninger:
$x_1=-6, y_1=-15 \\ x_2=2, y_2=1 $
Oppgave 4)
a)
$(a+2)^3-a\cdot(a+2)^2 \\ =(a+2)(a+2)^2-a\cdot(a+2)^2 \\ =(a+2)^2\cdot((a+2)-a) \\ =(a^2+4a+4)\cdot 2 \\ =2a^2+8a+8$
b)
$\frac{x+1}{x+2}-\frac{x+1}{x-1}-\frac{x+5}{x^2+x-2}$
$=\frac{(x+1)(x-1)}{(x+2)(x-1)}-\frac{(x+1)(x+2)}{(x-1)(x+2)}-\frac{x+5}{(x+2)(x-1)}$
$=\frac{x^2-1}{(x+2)(x-1)}-\frac{x^2+3x+2}{(x-1)(x+2)}-\frac{x+5}{(x+2)(x-1)}$
$=\frac{(x^2-1)-(x^2+3x+2)-(x+5)}{(x+2)(x-1)}$
$=\frac{x^2-1-x^2-3x-2-x-5}{(x+2)(x-1)}$
$=\frac{-4x-8}{(x+2)(x-1)}$
$=\frac{-4(x+2)}{(x+2)(x-1)}$
$=\frac{-4}{x-1}=\frac{4}{1-x}$
c)
$2lg(2x^2)+lg\frac{5}{x}-lg(2x^3)$
$2lg2+2lg(x^2)+lg5-lgx-(lg2+lg(x^3))$
$2lg2 + 4lgx + lg5 - lg x -lg 2 - 3lg x$
$lg 2 + lg 5 = lg (2\cdot5) = lg 10 = 1$
Oppgave 5)
a)
$\binom{7}{3} \cdot \binom{5}{2} = \frac{7\cdot6\cdot5}{3\cdot2\cdot1}\cdot\frac{5\cdot4}{2\cdot1}=35\cdot10=350$
Det er mulig å sette sammen 350 komiteer.
b)
P(Anne og Jens)$=\frac{3}{7}\cdot\frac{2}{5}=\frac{6}{35}$
Sannsynligheten for at både Anne og Jens blir med i komiteen er $\frac{6}{35}$
c)
P(Anne eller Jens) = P(Anne men ikke jens) + P(Jens men ikke Anne)
$=\frac{3}{7}\cdot\frac{3}{5}+\frac{4}{7}\cdot\frac{2}{5} \\ =\frac{9}{35}+\frac{8}{35}=\frac{17}{35}$
Sannsynligheten for at én av dem blir med i komiteen er $\frac{17}{35}$
Oppgave 6)
Kantene i Pascals trekant er alltid 1-ere. Ellers er et tall i Pascals trekant summen av de to tallene over. Utregning av de to midterste tallene som mangler:
$66-11=55$
$495-330=165$
Oppgave 7)
Opplysningene gir oss følgende likningssett, hvor x er prisen for skolegang for ett barn i én måned, og y er prisen for barnehjemsplass for ett barn i én måned.
<math> \left[ \begin{align*} 2x+y=700 \\ 4x+3y=1700 \end{align*}\right] </math>
Uttrykker likning I ved y:
$y=700-2x$
Setter inn verdien av y i likning II:
$4x+3(700-2x)=1700 \\ 4x+2100-6x=1700 \\ -2x = -400 \\ x=200$
Fra likning I:
$y=700-2\cdot 200=700-400=300$
Per barn per måned koster det 200kr for skolegang og 300kr for barnehjemsplass. For 20 barn blir det totalt:
$20\cdot 200kr + 20\cdot 300kr=4000+6000=10000$
Klassen til Kari må samle inn 10 000 kr hver måned.