R2 2020 vår LØSNING: Forskjell mellom sideversjoner
| Linje 286: | Linje 286: | ||
===b)=== | ===b)=== | ||
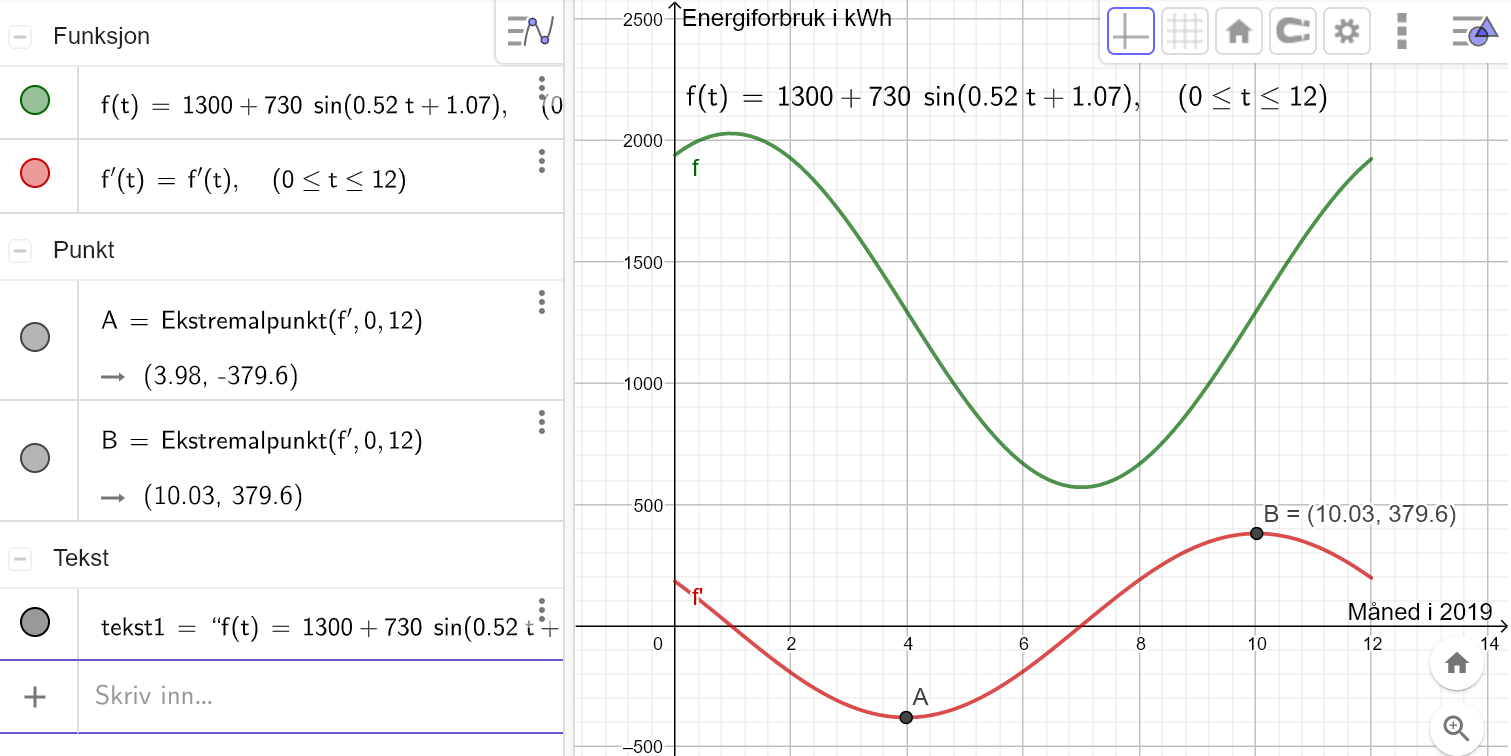
Bruker Geogebra til å tegne grafen til $f$ og $f'$ for $t\in[0,12]$. Finner toppunktet til $f'$ med kommandoen <i>Ekstremalpunkt</i> | Bruker Geogebra til å tegne grafen til $f$ og $f'$ for $t\in[0,12]$. Finner toppunktet til $f'$, punkt B, med kommandoen <i>Ekstremalpunkt</i>. x-verdien til punkt B er den samme som vendepunktet i den voksende delen av $f$. | ||
[[File: R2_V20_del2_1b.png]] | [[File: R2_V20_del2_1b.png]] | ||
| Linje 294: | Linje 294: | ||
===c)=== | ===c)=== | ||
=== | ===d)=== | ||
Sideversjonen fra 11. jul. 2020 kl. 08:16
Diskusjon av denne oppgaven på matteprat
Løsning del 1 av Kristian Saug
Løsning del 2 av Kristian Saug
Løsning del 1 og del 2 av Lektor Trandal
Løsningsforslag laget av Marius Nilsen ved Bergen Private Gymnas
DEL 1
Oppgave 1
a)
$f(x)=x\cdot sin x$
$f'(x)=sin x + x \cdot cos x$
b)
$g(x)=\frac{cos(x^2)}{x}$
$g'(x)=\frac{-2x\cdot sin(x^2)\cdot x - cos(x^2)\cdot 1}{x^2} = \frac{-2x^2 \cdot sin(x^2) - cos(x^2)}{x^2}$
Oppgave 2
a)
$\int(x^2+3+e^{2x})dx = \frac{1}{3}x^3+3x+\frac{1}{2}e^{2x}+C$
b)
Bruker variabelskifte, der $u=x^2$
$\frac{du}{dx}=2x \Rightarrow dx=\frac{du}{2x}$
$ \int 6x\cdot sin(x^2)dx = 3 \int 2x \cdot sin (u) \frac{du}{2x} = 3 \int sin(u) du = -3cos(u) + C = -3 cos(x^2)+C $
c)
Bruker delvis integrasjon, der $u = ln\,x \Rightarrow u'=\frac{1}{x}$ og $v' = x \Rightarrow v=\frac{1}{2}x^2$
Finner det ubestemte integralet:
$\int x \cdot ln\,x\,dx = \frac{1}{2}x^2 \cdot ln\,x- \int \frac{1}{x} \cdot \frac{1}{2}x^2 dx = \frac{1}{2}x^2 \cdot ln\,x -\frac{1}{2}\int x\, dx = \frac{1}{2}x^2 \cdot ln\,x -\frac{1}{4} x^2 + C$
Finner det bestemte integralet:
$\int_{1}^{e} x \cdot ln\,x\,dx = [\frac{1}{2}x^2 \cdot ln\,x -\frac{1}{4} x^2]_{1}^{e} = (\frac{1}{2}e^2 \cdot ln\,e -\frac{1}{4} e^2) - (\frac{1}{2}\cdot 1^2 \cdot ln\,1 -\frac{1}{4} \cdot 1^2) \\ = (\frac{2}{4}e^2 \cdot 1 - \frac{1}{4}e^2)-(\frac{1}{2} \cdot 0 - \frac{1}{4}) = \frac{1}{4}e^2+\frac{1}{4} $
Oppgave 3
a)
Finner $a_5$:
$S_5=\frac{a_1+a_5}{2}\cdot 5 \\ 55 = \frac{3+a_5}{2} \cdot 5 \\ a_5 = \frac{55}{5}\cdot 2 - 3 \\ a_5 = 19$
Finner differensen:
$d = \frac{a_5 - a_1}{5-1} \\ d = \frac{19-3}{4} \\ d= 4$
Finner $a_{10}$:
$a_{10} = a_1 + (10-1)\cdot d \\ a_{10} = 3 + 9\cdot 4 \\ a_{10} = 39$
Finner summen av de 10 første leddene:
$S_{10} = \frac{a_1+a_{10}}{2}\cdot 10 \\ S_{10} = \frac{3+39}{2}\cdot 10 \\ S_{10} = 210$
b)
Dersom $-1<k<1$ i en geometrisk tallfølge $a_n=a_1k^{n-1}$ sier vi at den konvergerer.
I slike tilfeller er $\lim_{n\to\infty}S_n=\frac{a_1}{1-k}$
I rekken $7 + \frac{7}{2} + \frac{7}{4}+...$ er $a_n = 7\cdot \frac{1}{2}^{n-1}$
Vi har $k = \frac{1}{2}$ og rekken konvergerer derfor.
Bestemmer summen av rekken:
$\lim_{n\to\infty}S_n=\frac{7}{1-\frac{1}{2}} = \frac{7}{\frac{1}{2}} = 14$
Oppgave 4
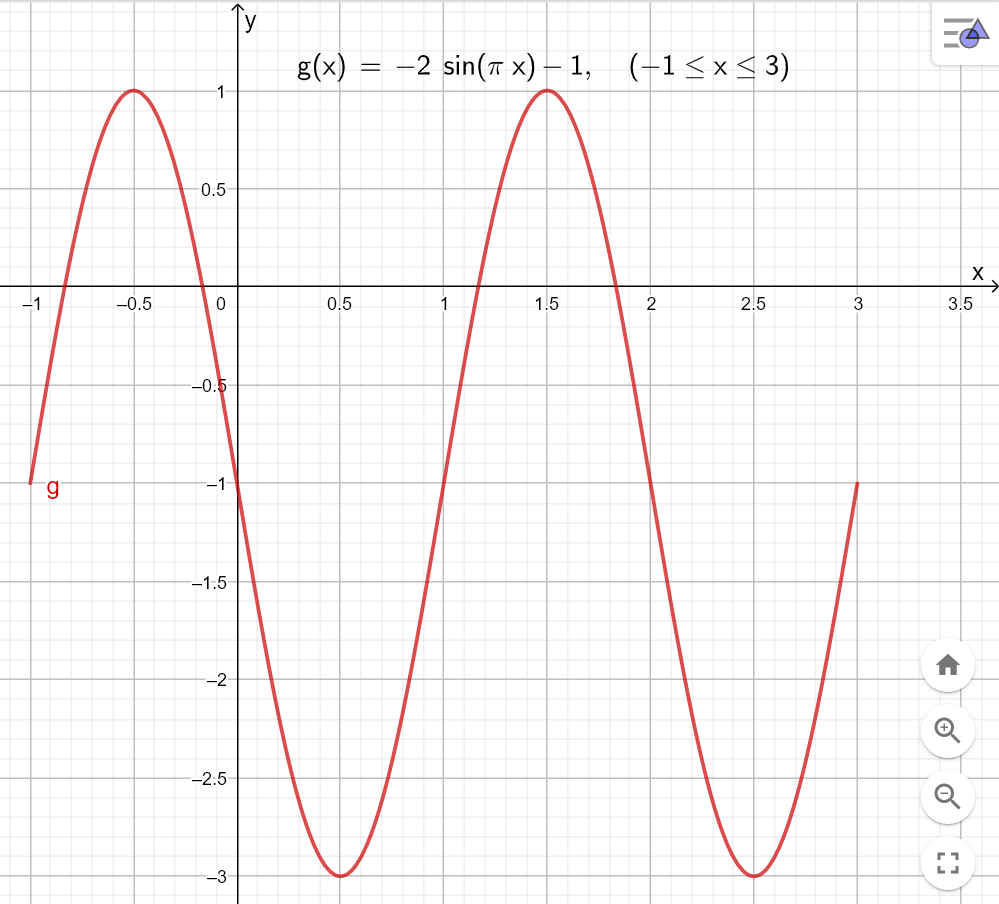
$f(x)=2 sin(\pi x + \pi)-1 \quad, \quad x\in \langle -1,3 \rangle$
a)
$f'(x)=2\pi cos(\pi x+ \pi) \quad, \quad x\in \langle -1,3 \rangle$
Setter $f'(x)=0$
$2\pi cos(\pi x+ \pi)=0 \\ cos(u) = 0 \Rightarrow u=\frac{\pi}{2} + k\pi \\ \pi x + \pi = \frac{\pi}{2} \vee \pi x +\pi = \frac{3\pi}{2} \vee \pi x + \pi = \frac{5\pi}{2} \vee \pi x + \pi = \frac{7\pi}{2} \\ x = -\frac{1}{2} \vee x = \frac{1}{2} \vee x = \frac{3}{2} \vee x = \frac{5}{2}$
Finner y-koordinatene til ekstremalpunktene (vet at en sinusfunksjon kun har topp- og bunnpunkter, og ingen terrassepunkter):
$f(-\frac{1}{2})= 2 sin(-\frac{\pi}{2} + \pi)-1 = 2 sin(\frac{\pi}{2})-1 = 2\cdot 1 - 1 = 1 $
$f(\frac{1}{2})= 2 sin(\frac{\pi}{2} + \pi)-1 = 2 sin(\frac{3\pi}{2})-1 = 2\cdot (-1) - 1 = -3 $
$f(\frac{3}{2})= 2 sin(\frac{3\pi}{2} + \pi)-1 = 2 sin(\frac{5\pi}{2})-1 = 2\cdot 1 - 1 = 1 $
$f(\frac{5}{2})= 2 sin(\frac{5\pi}{2} + \pi)-1 = 2 sin(\frac{7\pi}{2})-1 = 2\cdot (-1) - 1 = -3 $
Toppunkter: $(-\frac{1}{2}, 1)$ og $(\frac{3}{2}, 1)$
Bunnpunkter: $(\frac{1}{2}, -3)$ og $(\frac{5}{2}, -3)$
b)
Skjæring med y-aksen:
$f(0) = 2 sin (\pi\cdot 0 + \pi)-1 = 2 sin(\pi) - 1 = 0-1 =-1$
Grafen til $f$ skjærer y-aksen i punktet $(0,-1)$. Vi kan også se dette av funksjonsuttrykket.
Skjæring med x-aksen; setter $f(x)=0$
$2 sin(\pi x + \pi)-1 = 0 \\ sin(\pi x + \pi) = \frac{1}{2} \\ sin(u)=\frac{1}{2} \Rightarrow u=\frac{\pi}{6}+k\cdot 2\pi \vee u=\frac{5\pi}{6} + k\cdot 2\pi\\ \pi x + \pi = \frac{\pi}{6} \vee \pi x + \pi = \frac{5\pi}{6} \vee \pi x + \pi = \frac{13\pi}{6} \vee \pi x + \pi = \frac{17\pi}{6}\\ x= -\frac{5}{6}\vee x = -\frac{1}{6} \vee x= \frac{7}{6}\vee x = \frac{11}{6} $
Grafen til $f$ skjærer x-aksen i punktene $(-\frac{5}{6},0), (-\frac{1}{6},0),(\frac{7}{6},0),(\frac{11}{6},0)$.
c)
Bruk ekstremalpunktene og nullpunktene, samt skjæring med y-aksen, til å lage en skisse for hånd.
Oppgave 5
Vi har punktene A(-1,3,2), B(2,2,1), C(0,1,0) og T(5,3,8).
a)
$\vec{AB}=[2-(-1), 2-3, 1-2] = [3,-1,-1]$
$\vec{AC}=[0-(-1),1-3,0-2]=[1,-2,-2]$
$\vec{AB} \times \vec{AC} = [(-1)\cdot(-2)-(-1)\cdot(-2),(-1)\cdot 1 - 3\cdot(-2),3\cdot(-2)-(-1)\cdot 1] = [2-2,-1+6,-6+1] =[0,5,-5]$
b)
$\vec{AT}=[5-(-1), 3-3,8-2]=[6,0,6]$
$V=\frac{|(\vec{AB}\times \vec{AC}) \cdot \vec{AT}|}{6} = \frac{|[0,5,-5]\cdot[6,0,6]|}{6} = \frac{|0\cdot 6 + 5\cdot 0+(-5)\cdot 6|}{6} = \frac{|-30|}{6} =\frac{30}{6}= 5$
Volumet av pyramiden ABCT er 5.
c)
Likningen for et plan er
$ a(x-x_0)+b(y-y_0)+c(z-z_0)=0 $
Der a, b og c er koordinatene til planets normalvektor, og $(x_0,y_0,z_0)$ er et punkt i planet.
Vi har planets normalvektor $[0,5,-5]$ og et punkt i planet A(-1,3,2).
Vi får da likning for planet som inneholder punktene A, B og C:
$0(x-(-1))+5(y-3)+(-5)(z-2) = 0 \\ 5y-15 -5z + 10 =0 \\ 5y-5z=5 \\ y-z=1$
Oppgave 6
En uendelig geometrisk rekke er gitt ved
$2+ln\,x+\frac{(ln\,x)^2}{2}+...$
a)
Vi har kvotienten $k=\frac{ln\,x}{2}$. Rekken konvergerer når $\frac{ln\,x}{2} \in \langle -1, 1 \rangle$. Løser ulikhetene:
$\frac{ln\,x}{2}>-1 \\ ln\,x > -2 \\ x>e^{-2}$
og
$\frac{ln\,x}{2}<1 \\ ln\,x < 2 \\ x < e^{2}$
Rekken konvergerer når $x\in \langle e^{-2}, e^2\rangle$
b)
Summen av rekken er gitt ved
$S(x)=\frac{a_1}{1-k} \\ 4 = \frac{2}{1-\frac{ln\,x}{2}} \\ 4\cdot(1-\frac{ln\,x}{2})=2 \\ 4-2ln\,x=2 \\ 2ln\,x=2 \\ ln\,x=1 \\ x=e$
Summen av rekken blir 4 når $x=e$.
Oppgave 7
Vi har differensiallikningen $2x\cdot y'-3y=0$
Sjekker stigningstallet til tangenten i hvert av punktene:
Punkt A(2,2): $2\cdot 2 \cdot y' - 3\cdot 2 = 0 \\ 4y'-6= 0 \\ y'=\frac{3}{2}$
Punkt B(-2,2): $2\cdot(-2)\cdot y'-3\cdot 2 = 0 \\ -4y'-6=0 \\ y'=-\frac{3}{2}$
Punkt C(-2,-2): $2\cdot(-2)\cdot y'-3\cdot (-2) = 0 \\ -4y'+6=0 \\ y'=\frac{3}{2}$
Punkt D(2,-2): $2\cdot 2\cdot y'-3\cdot (-2) = 0 \\ 4y'+6=0 \\ y'=-\frac{3}{2}$
Den markerte tangentretningen samsvarer med retningen til tangenten til integralkurven som går gjennom punkt B og C, men ikke A og D. I punkt A viser den markerte tangentretningen stigningstall 0, og i punkt D stigningstall $-\frac{1}{4}$, noe som ikke passer med tangenten til integralkurven i disse to punktene.
Oppgave 8
Linje $l$, som står normalt på planet $\alpha$, gjennom punktet P(-3,7,-1):
$l: \left[ \begin{align*} x &=-3-2s \\ y &= 7+2s \\ z &= -1-s \end{align*}\right]$
Linja $m$, som står normalt på planet $\beta$, gjennom punktet Q(-4,5,-2):
$m: \left[ \begin{align*} x &=-4-7t \\ y &= 5+4t \\ z &= -2-4t \end{align*}\right]$
Skjæringspunktet mellom linje $l$ og $m$ er sentrum i kula. Finner skjæringspunktet S, ved å løse likningssettet:
$ I \quad \quad-3-2s =-4-7t \\ II \quad \quad 7+2s = 5+4t \\ III \quad -1-s = -2-4t $
Finner et uttrykk for s:
$III \quad s = 1+ 4t$
Setter inn uttrykket for s i likning $I$, og finner t:
$I \quad -3 -2(1+4t) = -4-7t \\ \quad \, \, -3-2-8t = -4-7t \\ \quad \quad t = -1$
Setter inn uttrykket for t i uttrykket for s fra likning $III$. (Dette for å kunne sjekke at likningssettet er riktig løst):
$s = 1 + 4\cdot(-1) = 1-4 = - 3$
Setter inn t = -1 i parameterfremstillingen for linje $m$, og finner punktet S:
$x = -4-7(-1) = -4 + 7 = 3 \\ y = 5+4(-1) = 5-4= 1 \\ z = -2-4(-1) = -2+4 = 2$
Sentrum i kula er S(3,1,2). Bestemmer radius til kula:
$\vec{QS} = [3-(-4), 1-5, 2-(-2)]=[7,-4,4]$
$|\vec{QS}|=\sqrt{7^2+(-4)^2+4^2} = \sqrt{49+16+16} = \sqrt{81} = 9$
Radius i kula er 9. Finner likning for kuleflaten:
$(x-3)^2+(y-1)^2+(z-2)^2=9^2$
Oppgave 9
En følge er gitt ved $a_1 = 2$ og $a_n = a_{n-1}+n$. Vi skal vise at $a_n=\frac{n^2+n+2}{2}$ for alle $n \in \N$.
1. Induksjonsgrunnlag: $n=1$ gir $a_1=\frac{1^2+1+2}{2} = \frac{4}{2} = 2$. Påstanden stemmer for $n=1$.
2. Induksjonstrinnet: Vi antar at $a_k=\frac{k^2+k+2}{2}$. Med $n = k+1$ får vi $a_{k+1}=\frac{(k+1)^2+(k+1)+2}{2}$, som vi skal vise.
Vi har $a_n=a_{n-1}+n$. Setter inn $n=k+1$:
$a_{k+1}=a_k+(k+1) \\ a_{k+1}=\frac{k^2+k+2}{2}+(k+1) \\ a_{k+1} = \frac{k^2+k+2}{2}+\frac{2k+2}{2} \\ a_{k+1} = \frac{k^2+2k+1+n+3}{2} \\ a_{k+1}= \frac{(k+1)^2+(k+1)+2}{2}$
Hvilket skulle vises.
DEL 2
Oppgave 1
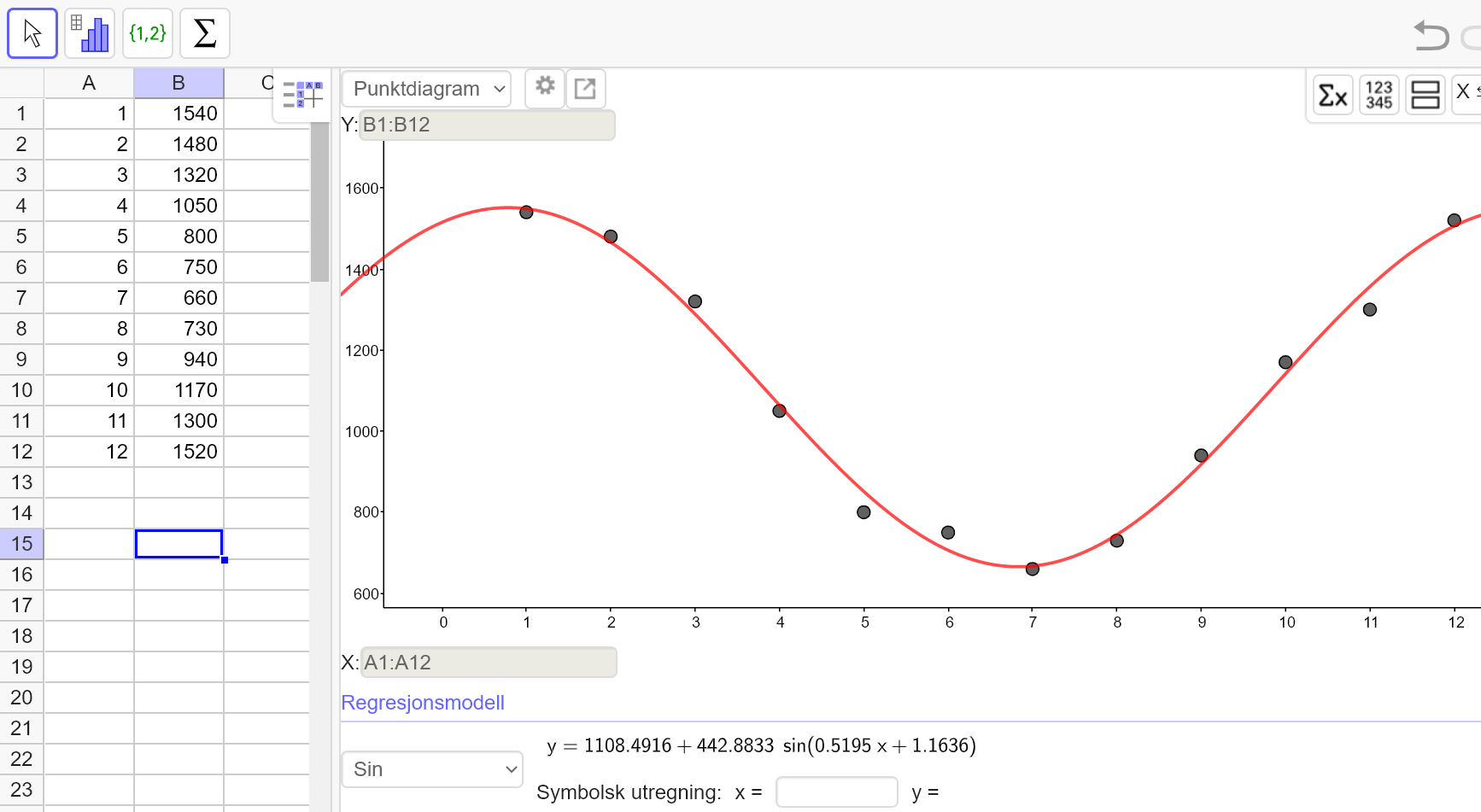
a)
Bruker Geogebra til å utføre en regresjonsanalyse.
En trigonometrisk funksjon som passer godt med informasjonen i tabellen er:
$f(x)=1108,5+442,8\cdot sin (0,52x+1,16)$
b)
Bruker Geogebra til å tegne grafen til $f$ og $f'$ for $t\in[0,12]$. Finner toppunktet til $f'$, punkt B, med kommandoen Ekstremalpunkt. x-verdien til punkt B er den samme som vendepunktet i den voksende delen av $f$.
Ifølge modellen økte forbruket raskest den 10. måneden, altså oktober.