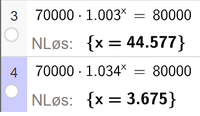S1 2022 Vår LK20 LØSNING

Oppgaven som pdf

Diskusjon av oppgaven på matteprat

Løsningsforslag laget av Farhan Omar

Løysing laga av Torodd F. Ottestad

DEL 1

Oppgave 1

$(2a)^{-1}\cdot (\frac{b}{2})^{-3}\cdot(a\cdot b)^3$

$=2^{-1}\cdot a^{-1}\cdot b^{-3}\cdot 2^3\cdot a^3 \cdot b^3$

$=2^{-1+3}\cdot a^{-1+3} \cdot b^{-3+3}$

$=2^2\cdot a^2 \cdot b^0$

$=4a^2$

Oppgave 2

$E(x)=0,2x+40+\frac{20\,000}{x}$

$E'(x)=0,2-\frac{20\,000}{x^2}$

$E'(100)=0,2-\frac{20\,000}{100^2} = 0,2-\frac{20\,000}{10\,000} = 0,2-2 =-1,8$

$E'(100)$ forteller oss at en dag det produseres 100 luer, ville produksjonskostnaden synke med 1,8 kroner per lue, dersom fabrikken skulle øke produksjonen med 1 lue.

Oppgave 3

$\lim\limits_{x \to 3} \frac{x-3}{x^2+x-12}$

$=\lim\limits_{x \to 3} \frac{x-3}{(x-3)(x+4)}$

$=\lim\limits_{x \to 3} \frac{1}{x+4}$

$=\frac{1}{7}$

Oppgave 4

$e^{2x}-e^x=2$

$(e^x)^2-e^x-2=0$

Setter $u=e^x$

$u^2-u-2=0$

$(u+1)(u-2)=0$

$u=-1 \vee u=2$

$e^x=-1 \vee e^x=2$

Forkaster det negative svaret fordi ln(-1) ikke er definert.

$ln(e^x)=ln(2)$

$x=ln(2)$

Oppgave 5

$lg(x+3)+lg\,x=lg\,a$

Setter inn x=7.

$lg(7+3)+lg\,7=lg\,a$

$lg\,10 + lg\,7=lg\,a$

$lg(10\cdot7)=lg\,a$

$lg\,70 = lg\,a$

$a=70$

Oppgave 6

a)

Eleven ønsker å finne ut hvor stor andel av en million kast med to terninger, som ender med at summen av de to terningene er 9 (i samme kast).

Linje 1: importerer "randint"-funksjonen fra "random"-biblioteket Linje 4: setter variabelen N til en million Linje 5: setter variabelen "gunstige" til null

Line 7: dette er en for-løkke, som går N ganger, altså en million ganger i dette tilfellet.

Linje 8-9 (inni for-løkka): to tilfeldige tall, a og b, genereres med "randint"-funksjonen. Tallene a og b er mellom 1 og 6 (tilsvarende 2 terninger).

Linje 10-11 (inni for-løkka): en if-setning sier at dersom summen av tallene a og b er lik 9, økes variabelen "gunstige" med 1.

Linje 13: her skrives andelen gunstige utfall ut, altså antall ganger summen av "terningene" ble 9, delt på antall forsøk (en million terningkast med to terninger).

b)

Sum 9 på to terninger er mulig å oppnå på 4 måter: 6+3, 5+4, 4+5, 3+6. Totalt er det 6*6=36 mulige utfall ved kast av to terninger.

Vi har at $P(sum\,9) = \frac{4}{36}=\frac{1}{9}$

DEL 2

Oppgave 1

a)

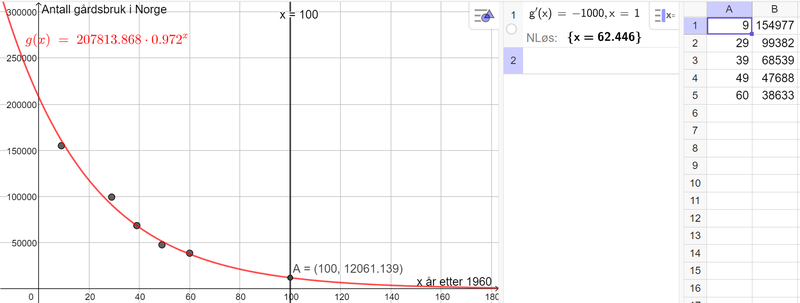
Velger å la x-verdiene være antall år etter 1960, og bruker regresjonsanalyse i Geogebra.

Velger en eksponentiell modell, da denne passer godt til dataene vi har. I tillegg er det usannsynlig at antall gårdsbruk i Norge blir null, så en eksponentiell modell hvor antall gårdsbruk fortsetter å avta uten å bli null, passer godt.

Modellen er $g(x)=207814\cdot 0,972^x$

b)

Skriver x=100 i Geogebra (tilsvarer 100 år etter 1960, altså 2060) og finner skjæringspunktet mellom x=100 og grafen til g. Se punkt A=(100,12061). Ifølge modellen min vil det være 12061 gårdsbruk i Norge i 2060.

c)

Bruker CAS i Geogebra og løser likningen $g'(x)=-1000$. CAS regner ut at $x=62,4$. Det vil si at ifølge modellen min, vil antall gårdsbruk i Norge avta med ca. 1000, ca. 62 år etter 1960, altså i år 2022.

Oppgave 2

a)

Vi må gå ut fra at:

- sannsynligheten for at en oppkjøring blir bestått, er en uavhengig hendelse (ulike oppkjøringer påvirker ikke hverandre)

- det er kun to utfall: bestått eller ikke bestått (dette kan vi trygt anta)

- det er en fast sannsynlighet for at en oppkjøring blir bestått (0,74)

b)

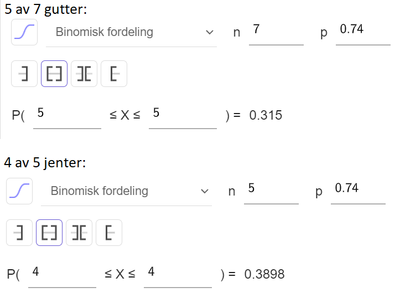
Bruker sannsynlighetskalkulatoren i Geogebra.

Sannsynligheten for at minst 8 av de 12 elevene består oppkjøringen er 0,821

c)

Bruker sannsynlighetskalkulatoren i Geogebra.

P(5 av 7 gutter OG 4 av 5 jenter) = 0,315*0,3898 = 0,123

Sannsynligheten for at akkurat 5 av guttene og akkurat 4 av jentene består oppkjøringen er 0,123

Oppgave 3

a)

Årlig vekstfaktor: $1,003^{12}=1,037$

Årlig rentesats er 3,7 %

b)

Bruker CAS i Geogebra.

Kan bruke månedlig eller årlig vekstfaktor. Det går ca. 44 måneder, eller 3 år og 8 måneder, før han har 80 000 kr på kontoen.

c)

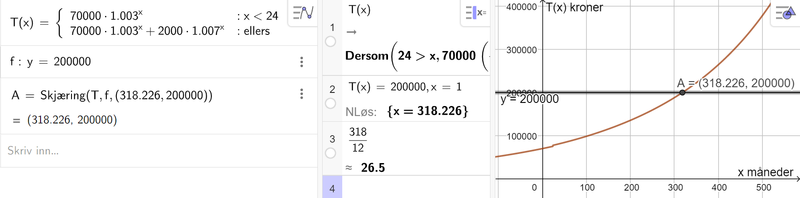
$ T(x) = \left\{\begin{array}{lr} 70000\cdot1,003^x & , & x <24 \\ 70000\cdot 1,003^x + 2000\cdot 1,007^x & , & x \geq 24 \end{array} \right.$

Funkjonen T(x) er ikke kontinuerlig for $x\in\mathbb{R}$. T(x) er en funksjon med delt forskrift. Grenseverdien når x går mot 24 (måneder) fra venstre, er ikke lik grenseverdien når x går mot 24 (måneder) fra høyre. Det betyr at funksjonen T er diskontinuerlig.

d)

Kan løse oppgaven grafisk og/eller i CAS. Her er begge deler vist.

Det tar ca. 318 måneder, eller 26,5 år, før T(x) blir større enn 200 000 kr.

Oppgave 4

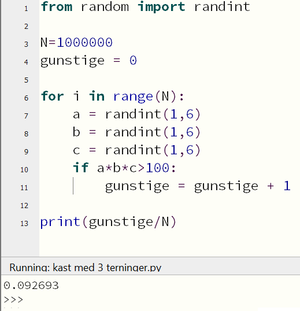
Her kan vi la oss inspirere av programmet i del 1, oppgave 6, med noen modifikasjoner.

Programmet simulerer en million kast med 3 terninger. Jeg kjører programmet flere ganger, og får hver gang en sannsynlighet for å vinne på rundt 0,092.

Oppgave 5

Bruker CAS i Geogebra.

Linje 1: definerer funksjonen til den rette linja som går gjennom punktene (0,2) og (2,0).

Linje 2: Definerer funksjonen for arealet av rektangelet. Jeg tenker at rektangelet består av to like deler. Arealet av delen til høyre for y-aksen, vil være bredden a ganget med høyden f(a). Jeg ganger dette med 2, for å få arealet av hele rektangelet.

Linje 3: Jeg setter den deriverte av T lik 0, for å finne den verdien av a som gir størst areal. (Jeg vet at ekstremalpunktet til T(a) er et toppunkt, fordi andregradsleddet er negativt).

Linje 4: den verdien av a som gir størst areal, er 1. Jeg beregner derfor arealet T(a) når a = 1.

Den største verdien T kan ha er 2.

Oppgave 6

Bruker CAS i Geogebra.

Det tar ca. 7,8 timer før temperaturen i kaffen er mindre enn 40 grader Celsius.

Oppgave 7

A er grafen til f, og D er grafen til f'. Der hvor grafen til f' har nullpunkter, har grafen til f ekstremalpunkter. Der hvor funksjonsverdien til f' er positiv, vokser grafen til f. Der hvor funksjonsverdien til f' er negativ, synker grafen til f. Der hvor grafen til f' har et bunnpunkt (f dobbeltderivert lik 0), har grafen til f et vendepunkt.

C er grafen til g, og B er grafen til g'. Der hvor grafen til g' har et nullpunkt, har grafen til g et ekstremalpunkt. Der hvor funksjonsverdien til g' er positiv, vokser grafen til g. Der hvor funksjonsverdien til g' er negativ, synker grafen til g.