Funksjonsdrøfting: Forskjell mellom sideversjoner
Ny side: Funksjonsutrykket f(x) <br> f(x) = 0 Løsningene av ligningen gir alle funksjonens nullpunkter (der grafen krysser x aksen). <br> Den deriverte f’(x) <br> f’(x) = 0 Løsningen av l... |
Ingen redigeringsforklaring |
||
| Linje 1: | Linje 1: | ||
===Funksjonsutrykket f(x)=== | |||
Funksjonsutrykket f(x) | |||
<br> | <br> | ||
f(x) = 0 Løsningene av ligningen gir alle funksjonens nullpunkter (der grafen krysser x aksen). | f(x) = 0 Løsningene av ligningen gir alle funksjonens nullpunkter (der grafen krysser x aksen). | ||
<br> | <br> | ||
Den deriverte f’(x) | ===Den deriverte f’(x)=== | ||
<br> | <br> | ||
f’(x) = 0 Løsningen av ligningen gir x verdiene for maksimums- eller minimumspunkter til f, også kalt ekstremalpunkter. Dersom f’(x) er positiv vokser f(x). Er f’(x) negativ avtar f(x). Grafen til f’(x) viser vekstforløpet til f(x). For å avgjøre om et ekstremalpunkt er et toppunkt eller et bunnpunkt lager man et fortegnsskjema. For å få med alle funksjonens ekstremalpunkter må man også sjekke punkter der funksjonen ikke er deriverbar, som knekkpunkter og endepunkter. | f’(x) = 0 Løsningen av ligningen gir x verdiene for maksimums- eller minimumspunkter til f, også kalt ekstremalpunkter. Dersom f’(x) er positiv vokser f(x). Er f’(x) negativ avtar f(x). Grafen til f’(x) viser vekstforløpet til f(x). For å avgjøre om et ekstremalpunkt er et toppunkt eller et bunnpunkt lager man et fortegnsskjema. For å få med alle funksjonens ekstremalpunkter må man også sjekke punkter der funksjonen ikke er deriverbar, som knekkpunkter og endepunkter. | ||
<br> | <br> | ||
Den dobbelderiverte f’’(x) | ===Den dobbelderiverte f’’(x) === | ||
<br> | <br> | ||
f’’(x) = 0 Løsningen av ligningen gir vendepunktet(ene) til f. Dersom den dobbelderiverte er en konstant har f ingen vendepunkter. Dersom den dobbelderiverte er negativ krummer grafen sin hule side nedover. Er den dobbelderiverte positiv vender grafen sin hule side oppover. | f’’(x) = 0 Løsningen av ligningen gir vendepunktet(ene) til f. Dersom den dobbelderiverte er en konstant har f ingen vendepunkter. Dersom den dobbelderiverte er negativ krummer grafen sin hule side nedover. Er den dobbelderiverte positiv vender grafen sin hule side oppover. | ||
| Linje 17: | Linje 16: | ||
[[Bilde:droefting.png]] | [[Bilde:droefting.png]] | ||
[[Category:derivasjon]] | |||
Sideversjonen fra 24. mar. 2009 kl. 08:10
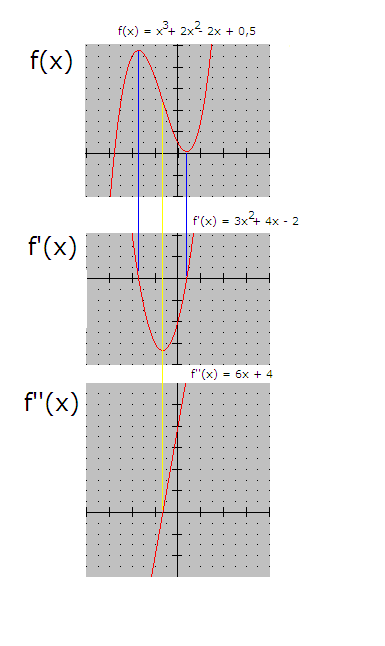
Funksjonsutrykket f(x)
f(x) = 0 Løsningene av ligningen gir alle funksjonens nullpunkter (der grafen krysser x aksen).
Den deriverte f’(x)
f’(x) = 0 Løsningen av ligningen gir x verdiene for maksimums- eller minimumspunkter til f, også kalt ekstremalpunkter. Dersom f’(x) er positiv vokser f(x). Er f’(x) negativ avtar f(x). Grafen til f’(x) viser vekstforløpet til f(x). For å avgjøre om et ekstremalpunkt er et toppunkt eller et bunnpunkt lager man et fortegnsskjema. For å få med alle funksjonens ekstremalpunkter må man også sjekke punkter der funksjonen ikke er deriverbar, som knekkpunkter og endepunkter.
Den dobbelderiverte f’’(x)
f’’(x) = 0 Løsningen av ligningen gir vendepunktet(ene) til f. Dersom den dobbelderiverte er en konstant har f ingen vendepunkter. Dersom den dobbelderiverte er negativ krummer grafen sin hule side nedover. Er den dobbelderiverte positiv vender grafen sin hule side oppover.
Eks. 1: