S1 2024 Vår LØSNING

Oppgaven som pdf

Diskusjon av oppgaven på matteprat

DEL 1

Oppgave 1

$f(x)=4x^2\cdot ln(3x)$

$f^{\prime }(x)=8x\cdot ln(3x)+4x^2\cdot \frac{1}{3x}\cdot 3$

$f^{\prime }(x)=8x\cdot ln(3x)+4x$

Oppgave 2

$(lnx{)}^2-lnx=6$

Setter $u=lnx$

$u^2-u-6=0$

$(u+2)(u-3)=0$

$u=-2\vee u=3$

$lnx=-2\vee lnx=3$

$x=e^{-2}\vee x=e^3$

$x=\frac{1}{e^2}\vee x=e^3$

Oppgave 3

$$f(x)=e^{-x+1},D_f=\mathbb{R}$$

$$\underset{x\to \mathrm{\infty }}{lim}{e}^{-x+1}=e^{-\mathrm{\infty }}=\frac{1}{e^{\mathrm{\infty }}}=0$$

$$\underset{x\to -\mathrm{\infty }}{lim}{e}^{-x+1}=e^{\mathrm{\infty }}=\mathrm{\infty }$$

Oppgave 4

a)

P(2 gule sokker) = $P(G)\cdot P(G|G)=\frac{6}{15}\cdot \frac{5}{14}=\frac{30}{15\cdot 14}=\frac{2}{14}=\frac{1}{7}$

b)

Det er 3*2*1 = 6 måter å trekke 3 sokker med ulik farge: GSH, GHS, HSG, HGS, SGH, SHG. Det er samme sannsynlighet for hver av disse.

P(3 ulike farger) = $6\cdot \frac{6\cdot 5\cdot 4}{15\cdot 14\cdot 13}=6\cdot \frac{2\cdot 4}{14\cdot 13}=\frac{24}{7\cdot 13}=\frac{24}{91}$

P(minst 2 sokker av samme farge) = 1 - P(3 ulike farger) = $1-\frac{24}{91}=\frac{67}{91}$

Oppgave 5

Vi endrer funksjons definisjonsområde til at 2 ikke er med i definisjonsmengden. :

$$f(x)=\{\begin{array}{l}x,0\le x<2\\ 5-x,2<x\le 5\end{array}$$

Vi har ivaretatt alle kravene:

$\bullet$ Verdimengden er uendret.

$\bullet$ Definisjonsmengden er så stor som mulig (uten å endre verdimengden)

$\bullet$ f er kontinuerlig. Vi sier at f er kontinuerlig hvis f er kontinuerlig for alle $a\in D_f$. Siden funksjonen f ikke er definert i punktet 2, så er f kontinuerlig i alle punkter i definisjonsmengden.

For nærmere forklaring, se s.129-131 i Aschehougs bok "Matematikk S1".

DEL 2

Oppgave 1

a)

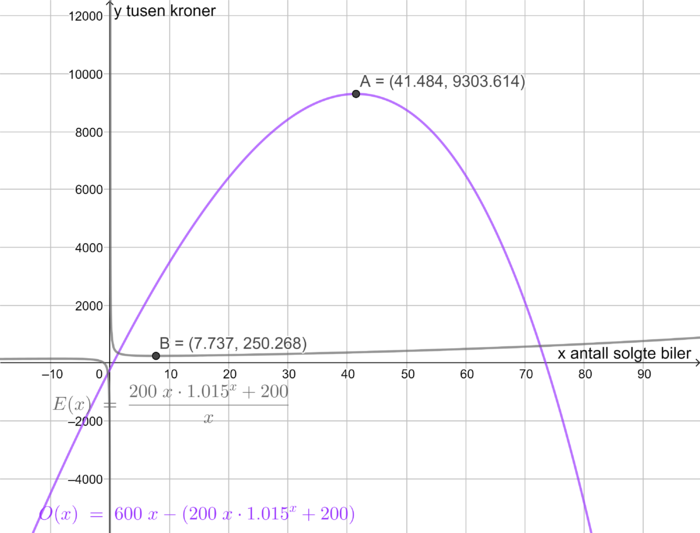
Tegner overskuddsfunksjonen O(x) i Geogebra, og bruker Ekstremalpunkt. Den produksjonsmengden som gir størst overskudd er ca. 41 biler, se punkt A.

b)

Tegner funksjonen E(x) for enhetskostnad. Produksjonsmengden som gir lavest mulig enhetskostnad er ca. 8 biler, se punkt B.

c)

De avtalte omtrent 784 234 kr per bil i denne kontrakten.