R2 2024 vår LØSNING

Oppgaven som pdf

Diskusjon av oppgaven på matteprat

Løsningsforslag Lektor Seland

DEL 1

Oppgave 1

$f(x)=-x^3+3x$

a)

${\int }_{-1}^{0}f(x)dx={\int }_{-1}^0(-x^3+3x)dx$

$=[-\frac{1}{4}{x}^4+\frac{3}{2}{x}^2{]}_{-1}^0$

$=0-(-\frac{1}{4}+\frac{3}{2})$

$=\frac{1}{4}-\frac{6}{4}$

$=-\frac{5}{4}$

b)

Finner nullpunktene til f:

$-x^3+3x=0$

$-x(x^2-3)=0$

$-x(x+\sqrt{3})(x-\sqrt{3})$

Nullpunkter: $x=-\sqrt{3},x=0,x=\sqrt{3}$

Vi har ingen nullpunkter i intervallene $[-1,0⟩$ og $⟨0,1]$

Beregner arealet av området avgrenset av grafen til f, x-aksen og linjene x=0 og x=1:

${\int }_0^{1}f(x)dx={\int }_0^1(-x^3+3x)dx$

$=[-\frac{1}{4}{x}^4+\frac{3}{2}{x}^2{]}_0^1$

$=(-\frac{1}{4}+\frac{3}{2})-0$

$=-\frac{1}{4}+\frac{6}{4}$

$=\frac{5}{4}$

Samlet areal er summen av arealene i intervallene $[-1,0]$ og $[0,1]$

$A=|-\frac{5}{4}|+\frac{5}{4}=\frac{10}{4}=\frac{5}{2}=2,5$

Arealet av området som er avgrenset av grafen til f, x-aksen og linjene x = −1 og x = 1 er 2,5.

Oppgave 2

Setter $u=sin(x)$. Da er $u^{\prime }=cos(x)$

$u^{\prime }=\frac{du}{dx}\Rightarrow dx=\frac{du}{u^{\prime }}$

$\int si{n}^3(x)\cdot cos(x)dx$

$=\int u^3\cdot u^{\prime }\frac{du}{u^{\prime }}$

$=\int u^{3}du$

$=\frac{1}{4}{u}^4+C$

$=\frac{1}{4}si{n}^4(x)+C$

Oppgave 3

a)

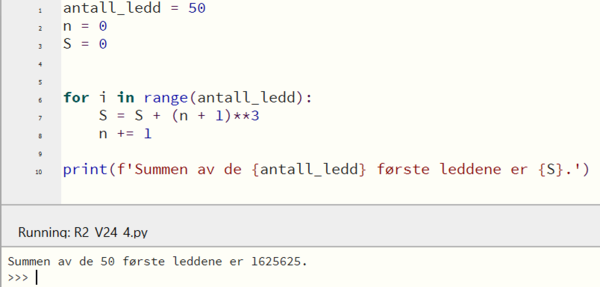
Eleven prøver å finne hvor mange ledd det trengs i en rekke før summen av rekken blir større enn 200. Hvert ledd er gitt ved $a_n=4n-2$, og første ledd har n=1.

b)

Vi har en aritmetisk rekke, fordi differansen mellom hvert ledd alltid er den samme (4 i dette tilfellet). Summen av en aritmetisk rekke er gitt ved $S=n\cdot \frac{a_1+a_n}{2}$

$n\cdot \frac{2+(4n-2)}{2}=200$

$\frac{4n^2}{2}=200$

$2n^2=200$

$n=\sqrt{100}$ (ingen negativ løsning fordi vi ser etter et positivt antall ledd)

$n=10$

Eleven får skrevet ut verdien 10, som vil si at det summen av de 10 første leddene i rekken er 200 eller mer.

Oppgave 4

a)

$\overrightarrow{AC}=[2-1,0-1,-1-0]=[1,-1,-1]$

$\overrightarrow{BC}=[2-4,0-1,-1-1]=[-2,-1,-2]$

$\overrightarrow{AC}\times \overrightarrow{BC}=[1,-1,-1]\times [-2,-1,-2]$

$=\left|\begin{array}{ccc}\overrightarrow{i}& \overrightarrow{j}& \overrightarrow{k}\\ 1& -1& -1\\ -2& -1& -2\end{array}\right|$

$=\overrightarrow{i}+4\overrightarrow{j}-3\overrightarrow{k}$

$=[1,4,-3]$

Arealet av paralellogrammet utspent av $\overrightarrow{AC}$ og $\overrightarrow{BC}$:

$|[1,4,-3]|=\sqrt{1^2+4^2+(-3{)}^2}=\sqrt{26}$

Arealet av trekant ABC:

$\frac{\sqrt{26}}{2}$

DEL 2

Oppgave 4

a)

$a_n=n^3$

$a_{n+1}=(n+1{)}^3$

Rekursiv formel for summen av rekken:

$S_{n+1}=S_n+a_{n+1}=S_n+(n+1{)}^3$

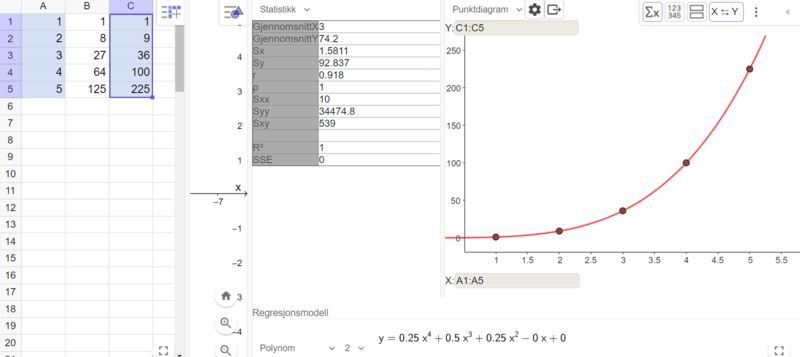
Eksplisitt formel for summen av rekken, finner vi ved regresjon i Geogebra:

$S_n=0,25n^4+0,5n^3+0,25n^2$

b)

c)

Vi skal bevise $S_n:1^3+2^3+3^3+...+n^3=0,25n^4+0,5n^3+0,25n^2$

Vi sjekker først om formelen stemmer for n=1 (se linje 2 i CAS). Formelen stemmer for n=1, siden $S_1=1^3=1$.

Vi antar nå at formelen stemmer for n = k, og sjekker om formelen stemmer for n = k + 1. Da vil $S_{k+1}=1^3+2^3+3^3+...+k^3+(k+1{)}^3=S_k+(k+1{)}^3$. Se linje 3 og 4 i CAS.

Vi har nå vist at dersom formelen stemmer for n=k , må den også stemme for n=k+1. Siden formelen stemmer for n=1, stemmer den for n=2, osv. $S_k\Rightarrow S_{k+1}$.