Integrasjon II

Det du leser her ligger utenfor pensum på vgs, men for interesserte elever kan det kanskje pirre nysgjerrigheten? Artikkelen er ikke ment å være en komplett lærebok, men en liten "teaser".

Forskjellen mellom dobbel og trippel integrasjon for volum

Både dobbel integrasjon og trippel integrasjon kan brukes til å beregne volum, men de anvendes i ulike situasjoner avhengig av hvordan volumet er beskrevet.

• Dobbel integrasjon

Brukes når volumet kan beskrives som området under en funksjon $z=f(x,y)$ over et gitt område i planet. Man må integrere over deler av ett av de tre akseplanene, xy, yz eller xz, samt plan som er paralelle med disse.

• Trippel integrasjon

Brukes når volumet må beskrives i hele rommet, dvs. når man jobber med en funksjon $f(x,y,z)$ innenfor et tredimensjonalt område.

Dobbel integrasjon brukes altså når høyden $z$ kan uttrykkes eksplisitt som en funksjon av $x$ og $y$, mens trippel integrasjon er nødvendig når volumet har en mer kompleks struktur i tre dimensjoner.

Dobbelintegrasjon: Grunnleggende prinsipper og anvendelser

Dobbelintegrasjon brukes for å beregne volum under en overflate, finne masse av tynne plater med variabel tetthet, og løse visse typer differensiallikninger.

Et dobbelintegral er av formen:

$${\int }_a^b{\int }_c^{d}f(x,y)dydx$$

Her integrerer vi først over $y$ -variabelen og deretter over $x$-variabelen. Vi integrerer alltid først det innerste integralet, så jobber vi oss utover (kan jo ha mer enn to integraler i hverandre).

Eksempel 1: Beregning av volum (av en kube)

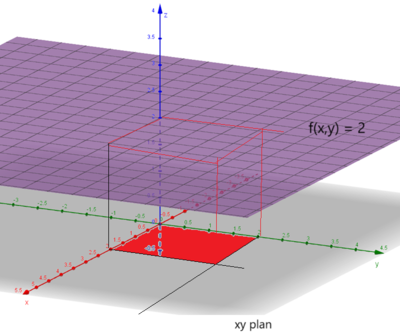
Vi ønsker å finne volumet av et område begrenset av xy- planet: $0\le x\le 2$ og $0\le y\le 2$ (Rødt område), og planet som er parallelt med xy planet og skjærer z- aksen i 2: $f(x,y)=2$.

$V=\int {\int }_{A}f(x,y)dydx={\int }_0^2{\int }_0^{2}2dydx={\int }_0^2[2y{]}_0^{2}dx={\int }_0^{2}4dx=[4x{]}_0^2=8$

Dette var jo som forventet. Vi integrerte over det røde området som er et 2x2 kvadrat (ikke la deg lure av perspektivet), multiplisert med høyden som er 2 gir jo det et volum på 8 enheter.

Eksempel 2: Beregning av volum under en overflate

Baugen på en seilbåt kan beskrives av funksjonen $f(x,y)=\frac{1}{2}{x}^2-\frac{1}{3}y$

Vi tenker at xy planet er havoverflaten og vi ønsker å beregne volumet av bauen, de 6 første fotene av båtens lengde.(Mindre båter oppgir oftest lengden i fot, ft.). Det volumet vi er på jakt etter ligger under xy planet og er avgrenset av $f(x,y)=\frac{1}{2}{x}^2-\frac{1}{3}y$.

Hva så med integrasjonsgrensene?

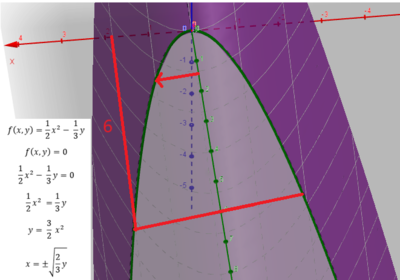
Vi har symmetri rund y aksen og integrerer fra 0 til f, og multipliserer med 2.

$$V=2{\int }_0^6{\int }_0^{(\frac{2}{3}y{)}^{\frac{1}{2}}}(\frac{1}{2}{x}^2+\frac{1}{3}y)dxdy$$

$$V=2{\int }_0^6[\frac{1}{6}{x}^3+\frac{1}{3}yx{]}_0^{(\frac{2}{3}y{)}^{\frac{1}{2}}}dy$$

$$V=2{\int }_0^6(\frac{1}{6}(\frac{2}{3}{)}^{\frac{3}{2}}{y}^{\frac{3}{2}}-\frac{1}{3}(\frac{2}{3}{)}^{\frac{1}{2}}{y}^{\frac{3}{2}})dy$$

$$V=2{\int }_0^6((\frac{1}{6}(\frac{2}{3}{)}^{\frac{3}{2}}-\frac{1}{3}(\frac{2}{3}{)}^{\frac{1}{2}})y^{\frac{3}{2}})dy$$

$$V=2[(\frac{1}{6}(\frac{2}{3}{)}^{\frac{3}{2}}-\frac{1}{3}(\frac{2}{3}{)}^{\frac{1}{2}})\cdot \frac{2}{5}\cdot y^{\frac{5}{2}}){]}_0^6$$

$$V=2(\frac{1}{6}(\frac{2}{3}{)}^{\frac{3}{2}}-\frac{1}{3}(\frac{2}{3}{)}^{\frac{1}{2}})\cdot \frac{2}{5}\cdot 6^{\frac{5}{2}})\approx -12,8$$

Man kan løse doble integraler i Geogebra, ved å løse de to integralene hver for seg

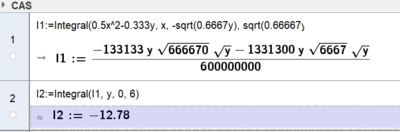
Integrasjonsrekkefølge

Å endre integrasjonsrekkefølgen i et dobbeltintegral kan være nyttig av flere grunner:

Forenkling av beregninger: Noen ganger er det lettere å evaluere integralet ved å bytte rekkefølge. For eksempel kan den indre integrasjonen bli enklere, eller det kan gjøre det mulig å bruke en kjent antiderivert.

Unngå vanskelige grenser: Når integrasjonsrekkefølgen endres, kan grensene for integralet ofte omskrives til en enklere form. Dette er spesielt nyttig hvis de opprinnelige grensene er kompliserte eller involverer vanskelige funksjoner.

Gjøre integralet løsbart: Noen ganger kan et dobbeltintegral være umulig eller svært vanskelig å løse i én rekkefølge, men mulig i en annen. Dette skjer ofte hvis integralet inneholder en funksjon som er vanskelig å integrere i én retning, men enkel i en annen.

Numerisk evaluering: I numeriske metoder kan det være mer effektivt å endre integrasjonsrekkefølgen for å redusere beregningskompleksiteten.

Teoretiske grunner: Noen ganger endres rekkefølgen for å illustrere en matematisk egenskap, for eksempel ved bruk av Fubinis teorem eller for å bevise likhet mellom forskjellige integraluttrykk.

Kort sagt, endring av integrasjonsrekkefølgen er et kraftig verktøy for å gjøre integraler enklere å håndtere, enten analytisk eller numerisk.

Eksempel på endring av integreringsrekkefølge for å forenkle beregninger

Vi vurderer det dobbeltintegralet:

$I={\int }_0^1{\int }_y^1{e}^{x^2}dxdy.$

1. Opprinnelig rekkefølge

Grensene sier at for en fast $y$, varierer $x$ fra $y$ til $1$. Problemet er at den indre integrasjonen

${\int }_y^1{e}^{x^2}dx$

har ingen elementær antiderivert, noe som gjør den vanskelig å løse direkte.

2. Endring av rekkefølge

Vi bytter integrasjonsrekkefølge ved å beskrive området på en annen måte:

• $x$ går fra $0$ til $1$.
• For en gitt $x$, varierer $y$ fra $0$ til $x$, fordi $y\le x$ i det opprinnelige integralet.

Dermed omskriver vi integralet som:

$I={\int }_0^1{\int }_0^x{e}^{x^2}dydx.$

Den indre integrasjonen er nå enkel:

${\int }_0^x{e}^{x^2}dy=e^{x^2}\cdot (x-0)=x{e}^{x^2}.$

Dermed reduseres integralet til:

$I={\int }_0^{1}x{e}^{x^2}dx.$

3. Løsning

Vi bruker substitusjon: Sett $u=x^2$, da er $du=2xdx$, eller $\frac{du}{2}=xdx$.

Grensene endres fra $x=0$ til $x=1$, som gir $u=0$ til $u=1$, så vi får:

$I={\int }_0^1{e}^u\frac{du}{2}=\frac{1}{2}{\int }_0^1{e}^{u}du.$

Dette løses enkelt:

$I=\frac{1}{2}{\left[e^u\right]}_0^1=\frac{1}{2}(e^1-e^0)=\frac{1}{2}(e-1).$

4. Konklusjon

Ved å bytte rekkefølge på integralet gikk vi fra et uløselig integral til et som enkelt kunne beregnes ved substitusjon. Dette viser hvorfor det kan være nyttig å endre integrasjonsrekkefølgen.

Trippelintegrasjon

En trippelintegral brukes til å beregne volum i rommet eller masse i et tredimensjonalt objekt. Generelt har vi:

$${\int }_a^b{\int }_c^d{\int }_e^{f}f(x,y,z)dzdydx$$

Her integrerer vi først over $z$, deretter $y$, og til slutt $x$.

Eksempel 4: Beregning av volum i en kube

Vi ønsker å finne volumet av en kube med sidelengde 1, altså området $0\le x\le 1$, $0\le y\le 1$, $0\le z\le 1$. Vi setter $f(x,y,z)=1$.

$V={\int }_0^1{\int }_0^1{\int }_0^{1}1dzdydx$

Integrerer først med hensyn til $z$:

${\int }_0^{1}1dz=z{|}_0^1=1$

Deretter med hensyn til $y$:

${\int }_0^{1}1dy=y{|}_0^1=1$

Til slutt med hensyn til $x$:

${\int }_0^{1}1dx=x{|}_0^1=1$

Så volumet er $1$ kubikkenhet.

Dobbelintegrasjon er et kraftig verktøy for å finne arealer, volum og masse i fysikk og matematikk. Den lar oss analysere hvordan en funksjon oppfører seg over et todimensjonalt område.

Eksempler på dobbel integrasjon

Eksempel 1: Volumet under en paraboloide

Finn volumet av området under paraboloiden $z=4-x^2-y^2$ over sirkelskiven $x^2+y^2\le 4$.

Løsning: Vi bruker polarkoordinater: $$V={\iint }_D(4-x^2-y^2)dA$$ I polarkoordinater ($x=r\cos \theta$, $y=r\sin \theta$): $$V={\int }_0^{2\pi }{\int }_0^2(4-r^2)rdrd\theta$$

Eksempel 2: Volum mellom to flater

Finn volumet mellom flatene $z=x^2+y^2$ og $z=2-x^2-y^2$ over området $x^2+y^2\le 1$.

Løsning: Volumet er gitt ved integralet: $$V={\iint }_D[(2-x^2-y^2)-(x^2+y^2)]dA$$ I polarkoordinater: $$V={\int }_0^{2\pi }{\int }_0^1(2-2r^2)rdrd\theta$$

Trippel integrasjon

Eksempel 3: Volum av en kule

Finn volumet av en kule med radius $R$, gitt ved $x^2+y^2+z^2\le R^2$.

Løsning: Bruk kulekoordinater ($x=r\sin \theta \cos \varphi$, $y=r\sin \theta \sin \varphi$, $z=r\cos \theta$): $$V={\int }_0^{2\pi }{\int }_0^{\pi }{\int }_0^R{r}^2\sin \theta drd\theta d\varphi$$

Eksempel 4: Volum av et tetraeder

Finn volumet av tetraederet med hjørner i $(0,0,0)$, $(a,0,0)$, $(0,b,0)$ og $(0,0,c)$.

Løsning: Integrasjonsgrenser bestemmes av planlikningen $\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1$, så volumet er: $$V={\int }_0^a{\int }_0^{b(1-x/a)}{\int }_0^{c(1-x/a-y/b)}dzdydx$$