Komplekse tall

\[Z =a + ib\]

• a kalles for realdelen og skrives ofte a = Re(Z)

• b kalles for imaginærdelen og skrives ofte b = Im(Z)

Mengden av alle komplekse tall kalles for $\mathbb{C}$. De reelle tallene er inkludert i $\mathbb{C}$.

$Z = a + ib$ er formen komplekse tall skrives på. a og b er reelle tall mens i er den imaginære enheten. <math>i^2</math> er størrelsen som tilfredsstiller $i^2= -1$.

\[ i^2 = -1 \] \[\sqrt{ -1} = i\].

Det betyr at andregradslikninger alltid har en løsning innenfor tallmengden $\mathbb{C}$.

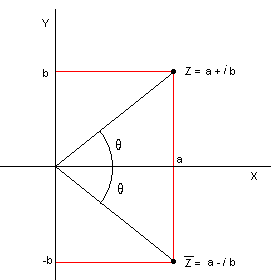
For å visualisere de komplekse tallene kan vi bruke XY planet. Vi setter a =X og b = Y. Det komplekse planet C ser da slik ut:

REGNEREGLER FOR KOMPLEKSE TALL

Addisjon

Summering av to komplekse tall gjøres ved å summere realdelen for seg og imaginærdelen for seg. Dersom vi skal summere <math>Z_1 = 1 + 2i \quad og \quad Z_2 = 2 + 2i</math> blir resultatet <math>Z_3 = 3 + 4i</math>

Generelt kan summen av det komplekse tallene \[ Z = a + ib \] og \[ W = c + id \] uttrykkes som \[ Z + W = (a + c) + i(b + d) \]

Vi kan oppfatte de komplekse tallene som vektorer i det komplekse plan. Regneoperasjonen over kan da fremstilles slik;

Eksempel

\[Z_1 = 1 + 2i \quad og \quad Z_2 = 2 + 2i \]

\[Z_3 = Z_1 + Z_2 = (1+2i) + (2+2i) = (1+2) + (2+2)i = 3+4i \]

Subtraksjon

Generelt kan differansen av det komplekse tallene \[ Z = a + ib \] og \[ W = c + id \] uttrykkes som \[ Z - W = (a - c) + i(b - d) \]

Den imaginære enheten i som potens av forskjellig grad

Den imaginære enheten i er definert som: <math> i = \sqrt{-1} </math> . Den har spesielle egenskaper når den opphøyes i ulike potenser, og det finnes et periodisk mønster:

Grunnleggende egenskaper

• \[ i^1 = i \]
• \[i^2 = -1 \]
• \[i^3 = i^2 \cdot i = (-1) \cdot i = -i \]
• \[i^4 = i^3 \cdot i = (-i) \cdot i = -i^2 = -(-1) = 1 \]

Periodisitet

Vi ser at etter fire potenser gjentar mønsteret seg: \[ i^5 = i^1 = i, \quad i^6 = i^2 = -1, \quad i^7 = i^3 = -i, \quad i^8 = i^4 = 1 \]

Dermed kan vi generelt si at:

Generelt:

\[ i^n = \begin{cases} i, & \text{hvis } n \equiv 1 \pmod{4} \\ -1, & \text{hvis } n \equiv 2 \pmod{4} \\ -i, & \text{hvis } n \equiv 3 \pmod{4} \\ 1, & \text{hvis } n \equiv 0 \pmod{4} \end{cases} \]

Eksempl:

• <math> i^{10} </math>: Siden <math> 10 \equiv 2 \pmod{4} </math>, har vi <math> i^{10} = -1 </math>.
• <math> i^{15} </math>: Siden <math> 15 \equiv 3 \pmod{4} </math>, har vi <math> i^{15} = -i </math>.
• <math> i^{20} </math>: Siden <math> 20 \equiv 0 \pmod{4} </math>, har vi <math> i^{20} = 1 </math>.

Dette mønsteret kan brukes til raskt å finne verdien av <math> i^n </math> for enhver eksponent n.

Multiplikasjon.

Multiplikasjon utføres på vanlig måte: \[ (a + bi)(c + di) = ac + adi + bci + bdi^2 = (ac - bd) + (ad + bc)i \]

Fordi

\[ bdi^2 = bd \cdot(-1) = -bd \]

Eksempel: Regn ut \((2 + 3i) \cdot (4 - i)\)

Løsning: \[ (2 + 3i)(4 - i) = 2\cdot4 + 2\cdot(-i) + 3i\cdot4 + 3i\cdot(-i) \] \[ = 8 - 2i + 12i - 3i^2 \] \[ = 8 + 10i - (-3) \] \[ = 11 + 10i \]

Komplekskonjugert

Den komplekskonjugerte til et komplekst tall er et annet komplekst tall som har samme reelle del, men den imaginære delen med motsatt fortegn.

Gitt et komplekst tall:

z = a + bi

hvor a og b er reelle tall og i er den imaginære enheten (i² = -1), så er den komplekskonjugerte:

z̅ = a - bi

Notasjon

Den komplekskonjugerte skrives ofte som:

• ȳ (med en strek over symbolet)
• conj(z)
• z*

Eksempler

1. z = 3 + 4i → z̅ = 3 - 4i
2. z = -2 - 7i → z̅ = -2 + 7i
3. z = 5 → z̅ = 5 (reelle tall er uendrede ved konjugering)
4. z = 0 + 6i → z̅ = 0 - 6i = -6i

Bruksområder

• Divisjon med komplekse tall: Når man skal dividere komplekse tall, brukes den komplekskonjugerte for å "rense" nevneren.

Eksempel: (1 + i)/(2 - 3i) → multipliser teller og nevner med den komplekskonjugerte av nevneren: (2 + 3i).

• Absoluttverdi/modul av et komplekst tall: |z|² = z * z̅
• Løsning av ligninger i kompleks analyse og elektriske kretser.
• Signalbehandling og Fourier-transformasjon: brukes til å analysere frekvenskomponenter og kompleksverdier i signaler.

Lengden av linjestykket <math>OZ_n</math> kan vi finne ved å bruke Pytagoras. Lengden er gitt ved <math>|Z_n| = \sqrt{a^2 + b^2}</math>. <math>|Z_n|</math> kalles absoluttverdien eller modulen av det komplekse tallet <math>Z_n</math>

Subtraksjon utføres ved å subtrahere realdelen for seg og imaginærdelen for seg, altså analogt til addisjon. Generelt har vi

Z - W = (a - c) + i(b - d)

Vi kan oppgi det komplekse tallet som et produkt av lengden <math>OZ_n</math> og vinkelen mellom X aksen og linjestykket <math>OZ_n</math>.

Fra figuren over ser vi at Z kan utrykkes som lengden av OZ og θ. Dersom vi kaller absoluttverdien av Z for r får vi :

Z = r(cos θ + isin θ). θ kalles argumentet til Z og skrives arg Z. Argumentet til Z er entydig bestemt i [0,2π >

punktet <math> \overline{Z}= a-bi</math> kalles det konjugerte komplekse tallet til Z.

en viktig egenskap er:

<math>Z \cdot \overline{Z} = a^2 + b^2 =|Z|^2</math>

Divisjon.

Vi multipliserer teller og nevner med det konjugerte komplekse tallet til nevneren. Da får vi et reelt tall i nevneren:

<math>\frac{a+bi}{c+di} = \frac{(a+bi)(c-di)}{(c+di)(c-di)} = \frac {ac-adi +bci -bdi^2}{c^2 -cdi + cdi -d^2i^2}= \frac {ac+bd -(ad-bc)i}{c^2 + d^2}</math>

Konjugering og modulus

Komplekse konjugatet av $z = a + bi$ er: \[ \overline{z} = a - bi \]

Modulus av <math>z</math> er: \[ |z| = \sqrt{a^2 + b^2} \]

Eksempel: \[ |3 + 4i| = \sqrt{3^2 + 4^2} = 5 \]

Divisjon

For å dele <math>z_1</math> med <math>z_2</math>, multipliserer vi med konjugatet av nevneren: <math>

�rac{z_1}{z_2} = �rac{(a + bi)}{(c + di)} 	imes �rac{(c - di)}{(c - di)}

</math> Eksempel: <math>

�rac{3 + 2i}{1 - i} = �rac{(3+2i)(1+i)}{(1-i)(1+i)} = �rac{1 + 5i}{2} = �rac{1}{2} + �rac{5}{2}i

</math>

.

Polarform

Ethvert komplekst tall kan skrives som: <math>

z = r(\cos 	heta + i \sin 	heta)

</math> Der: <math>

r = |z| = \sqrt{a^2 + b^2}, \quad 	heta = 	an^{-1} \left( �rac{b}{a} \right)

</math>

Eksempel: <math>

z = 1 + i \Rightarrow r = \sqrt{2}, \quad 	heta = �rac{\pi}{4}

</math>

Eulers formel og eksponentiell representasjon

Eulers formel: <math> e^{i heta} = \cos heta + i \sin heta </math>

Polarformen kan derfor skrives som: <math> z = r e^{i heta} </math>

De Moivres teorem og røtter

De Moivres teorem:

1. 1. 1. **De Moivres teorem**

De Moivres teorem er et viktig resultat i kompleks analyse som sier at for enhver kompleks tall \( z \) skrevet på polar form og for et heltall \( n \), gjelder følgende:

\[ (\cos \theta + i \sin \theta)^n = \cos(n\theta) + i \sin(n\theta) \]

Alternativt kan dette skrives med eksponentiell notasjon ved hjelp av Eulers formel \( e^{i\theta} = \cos\theta + i\sin\theta \):

\[ (e^{i\theta})^n = e^{in\theta} \]

Dette betyr at for et komplekst tall på polar form, \( z = r e^{i\theta} \), har vi:

\[ z^n = r^n e^{in\theta} = r^n (\cos(n\theta) + i\sin(n\theta)) \]

1. 1. 1. **Bruksområder**

1. **Beregning av potenser av komplekse tall**

  - Hvis du har et komplekst tall \( z = r(\cos\theta + i\sin\theta) \), kan du raskt finne \( z^n \) ved å opphøye modulus til \( n \) og multiplisere argumentet med \( n \).  

2. **Røtter av komplekse tall**

  - De Moivres teorem hjelper med å finne de \( n \)-te røttene av komplekse tall. En kompleks \( n \)-te rot av \( r e^{i\theta} \) er gitt ved:

    \[
    w_k = r^{1/n} e^{i(\theta + 2\pi k)/n}, \quad k = 0, 1, 2, ..., n-1
    \]

    Dette viser at et komplekst tall har \( n \) distinkte \( n \)-te røtter, jevnt fordelt langs en sirkel i det komplekse planet.

1. 1. 1. **Eksempel**

La oss si vi ønsker å beregne \( (1 + i)^4 \). Først skriver vi \( 1 + i \) på polar form:

\[ r = \sqrt{1^2 + 1^2} = \sqrt{2}, \quad \theta = \tan^{-1}(1/1) = \frac{\pi}{4} \]

Ved å bruke De Moivres teorem:

\[ (1 + i)^4 = (\sqrt{2})^4 \left(\cos\left(4 \times \frac{\pi}{4}\right) + i \sin\left(4 \times \frac{\pi}{4}\right)\right) \]

\[ = 4 (\cos \pi + i \sin \pi) = 4(-1 + 0i) = -4 \]

1. 1. 1. **Oppsummering**

De Moivres teorem gir en elegant metode for å beregne potenser og røtter av komplekse tall, noe som er spesielt nyttig i ingeniørfag, fysikk og signalbehandling.

<math> (\cos heta + i \sin heta)^n = \cos(n heta) + i\sin(n heta) </math>

Generell formel for <math>n</math>-te røtter:

<math> z_k = r^{1/n} e^{i( heta + 2\pi k)/n}, \quad k = 0, 1, ..., n-1 </math>

Eksempel: Kvadratroten av <math>i</math>:

<math> \sqrt{i} = e^{i\pi/4} = \pm \left(�rac{\sqrt{2}}{2} + i�rac{\sqrt{2}}{2} \right) </math>

Oppgaver med komplekse tall

Eksempel 1: Regn ut \((3 + 4i) + (5 - 2i)\)

Løsning: \[ (3 + 4i) + (5 - 2i) = 3 + 5 + (4i - 2i) = 8 + 2i \]

Eksempel Subtraksjon Regn ut \((7 + 6i) - (2 + 3i)\)

Løsning: \[ (7 + 6i) - (2 + 3i) = (7 - 2) + (6i - 3i) = 5 + 3i \]

Oppgave 4: Divisjon

Regn ut \(\frac{5 + 2i}{3 - i}\)

Løsning: Multipliser teller og nevner med den konjugerte av nevneren: \[ \frac{(5 + 2i)(3 + i)}{(3 - i)(3 + i)} \] Beregning: \[ 5\cdot3 + 5\cdot i + 2i\cdot3 + 2i\cdot i = 15 + 5i + 6i + 2i^2 \] \[ = 15 + 11i - 2 \] \[ = 13 + 11i \] Nevner: \[ (3 - i)(3 + i) = 9 - i^2 = 9 + 1 = 10 \] Endelig svar: \[ \frac{13 + 11i}{10} = 1.3 + 1.1i \]

Oppgave 5: Potenser

Regn ut \((1 + i)^4\)

Løsning: Bruk binomialteoremet eller direkte utregning: \[ (1 + i)^2 = 1 + 2i + i^2 = 1 + 2i - 1 = 2i \] \[ (2i)^2 = 4i^2 = -4 \]

Oppgave 6: Kvadratrot

Regn ut \(\sqrt{-9}\)

Løsning: \[ \sqrt{-9} = \sqrt{9} \cdot \sqrt{-1} = 3i \]

Oppgave 7: Eulers form

Skriv \(1 + i\) på polarform.

Løsning: \[

r = \sqrt{1^2 + 1^2} = \sqrt{2}, \theta = \tan^{-1}(1) = \frac{\pi}{4}

\] \[ 1 + i = \sqrt{2} e^{i\pi/4} \]

Oppgave 8: Eksponentiell form

Regn ut \(e^{i\pi/2}\)

Løsning: Ved Eulers formel: \[

e^{i\pi/2} = \cos(\pi/2) + i\sin(\pi/2) = i

\]

Oppgave 9: Kubikkrot

Finn en kubikkrot av \(8\).

Løsning: Vi løser \(z^3 = 8\): \[ 8 = 8e^{i0}, \text{ kubikkrot gir } 2e^{i0/3} = 2 \]

Oppgave 10: De Moivres teorem

Regn ut \((\cos \frac{\pi}{3} + i \sin \frac{\pi}{3})^5\)

Løsning: Bruk De Moivres teorem: \[

(\cos \frac{\pi}{3} + i \sin \frac{\pi}{3})^5 = \cos \frac{5\pi}{3} + i \sin \frac{5\pi}{3}

\] \[

= \cos(-\frac{\pi}{3}) + i \sin(-\frac{\pi}{3})

\] \[

= \frac{1}{2} - i \frac{\sqrt{3}}{2}

\]