1T 2012 vår LØSNING: Forskjell mellom sideversjoner
Fra Matematikk.net
Ingen redigeringsforklaring |
|||
| Linje 3: | Linje 3: | ||
== a) == | === a) === | ||
<p></p> | <p></p> | ||
1) <tex> 8+2 \cdot 3 - 3^2 - (10-12)^2 = 8 + 6 - 9 -4 =1</tex> | 1) <tex> 8+2 \cdot 3 - 3^2 - (10-12)^2 = 8 + 6 - 9 -4 =1</tex> | ||
| Linje 12: | Linje 12: | ||
== b) == | === b) === | ||
<p></p> | <p></p> | ||
<tex>5,5 \cdot 10^5 \cdot 6,0 \cdot 10^6 = 5,5 \cdot 6,0 \cdot 10^{11} =33,0 \cdot 10^{11} = 3,3 \cdot 10^{12} </tex><p></p> | <tex>5,5 \cdot 10^5 \cdot 6,0 \cdot 10^6 = 5,5 \cdot 6,0 \cdot 10^{11} =33,0 \cdot 10^{11} = 3,3 \cdot 10^{12} </tex><p></p> | ||
== c) == | === c) === | ||
<p></p> | <p></p> | ||
<tex>\left[{ x+2y =16 \\ 3x-y=6 }\right] \\ \left[{ x =16-2y \\ 3(16-2y)-y=6 }\right] \\ | <tex>\left[{ x+2y =16 \\ 3x-y=6 }\right] \\ \left[{ x =16-2y \\ 3(16-2y)-y=6 }\right] \\ | ||
| Linje 23: | Linje 23: | ||
<p></p> | <p></p> | ||
== d) == | === d) === | ||
<p></p> <tex>2x-3=6- \frac 14x</tex><p></p> | <p></p> <tex>2x-3=6- \frac 14x</tex><p></p> | ||
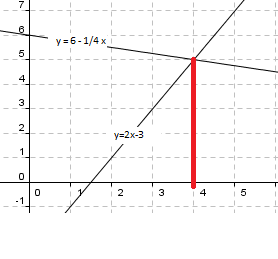
Grafisk løsning<p></p>[[Fil:1t-2012,1.png]] | Grafisk løsning<p></p>[[Fil:1t-2012,1.png]] | ||
Sideversjonen fra 31. mai 2012 kl. 05:44
Opgave 1
a)
1) <tex> 8+2 \cdot 3 - 3^2 - (10-12)^2 = 8 + 6 - 9 -4 =1</tex>
2)
<tex> \frac{9^{\frac 12} \cdot 3^{-3}}{(3^{-2})^3} = \frac{(3^2)^{\frac 12} \cdot 3^{-3}}{3^{-6}} = 3^{1-3+6} =3^4 = 81 </tex>
b)
<tex>5,5 \cdot 10^5 \cdot 6,0 \cdot 10^6 = 5,5 \cdot 6,0 \cdot 10^{11} =33,0 \cdot 10^{11} = 3,3 \cdot 10^{12} </tex>
c)
<tex>\left[{ x+2y =16 \\ 3x-y=6 }\right] \\ \left[{ x =16-2y \\ 3(16-2y)-y=6 }\right] \\ \left[{ x =16-2y \\ 48-6y-y=6 } \right] \\ \left[{ x =16-2y \\ y=7 } \right] \\ \left[{ x = 2 \\ y=7 } \right] </tex>
d)
<tex>2x-3=6- \frac 14x</tex>
Grafisk løsning
Man observerer at: x = 4
e)
<tex>-x^2-x+13 \geq 0</tex>
Faktoriserer (abc-formelen) og får:
<tex>-(x+4)(x-3) \geq 0</tex>
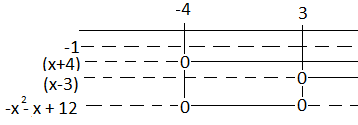
Fortegnsskjema:
<tex> x \in [-4,3]</tex>