Bevis for cosinussetningen

Man må vise at setningen gjelder både for spissvinklede og stompvinklede trekanter.

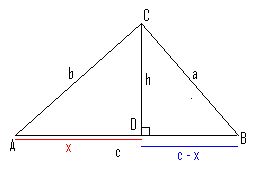
Spissvinklede:

Bruker pytagoras på trekanten ADC:

$x^2+h^2=b^2\Rightarrow h^2=b^2-x^2$

Bruker pytagoras på trekanten DBC:

$h^2+(c-x{)}^2=a^2$

Kombinerer de to utrykkene ved å sette inn for h i andre:

<math> b^2 - x^2 + c^2 - 2cx + x^2 =a^2< /math> < math>a^2 = b^2 + c^2 -2cx< /math>

Finner cosA:

$cosA=\frac{x}{b}\Rightarrow x=b\cdot cosA$

og får:

$a^2=b^2+c^2-2bccosA$

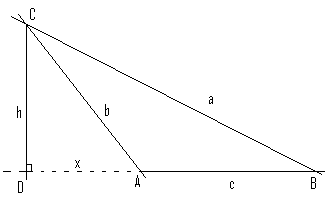
Stompvinklede:

Bruker pytagoras på trekanten DBC:

$$\begin{gathered} a^2=h^2+(c+x{)}^2 \\ {a}^2=h^2+c^2+2cx+x^2 \end{gathered}$$

Bruker pytagoras på trekanten DAC:

$b^2=x^2+h^2\Rightarrow h^2=b^2-x^2$

Kombinere resultatene og får:

$$\begin{gathered} a^2=b^2-x^2+c^2+2cx+x^2 \\ {a}^2=b^2+c^2+2cx \end{gathered}$$

Fra enhetssirkelen har man at cosA = -cos(180-A). Da får man:

$cos(180-A)=-cosA=\frac{x}{b}\Rightarrow x=-bcosA$ som gir:

$a^2=b^2+c^2-2bccosA$

---