R2 2011 høst LØSNING: Forskjell mellom sideversjoner
| Linje 65: | Linje 65: | ||
= Del 2 = | = Del 2 = | ||
== Oppgave 2 == | |||
=== a) === | |||
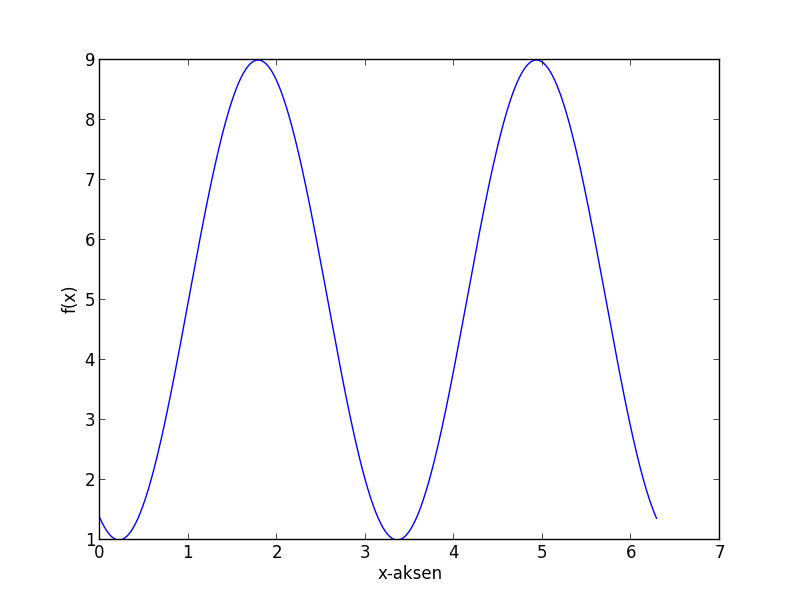
[[Bilde:Funksjon1.png]] | |||
Sideversjonen fra 24. apr. 2013 kl. 23:29
Del 1
Oppgave 1
a)
1) Produktregelen gir at $f(x)=xe^x\Rightarrow f'(x) = e^x+xe^x = (1+x)e^x$.
2) Kjerneregelen gir at $g(x)=2\sin 2x \Rightarrow g'(x) = 4\cos 2x$.
3) Kjerneregelen gir at $h(x)=2\sin^2 x \Rightarrow h'(x) = 4\sin x \cos x$
b)
1) Delvis integrasjon gir at $\int x\cos x \, dx = x\sin x - \int \sin x\, dx = x\sin x +\cos x + C$ med integrasjonskonstant $C$.
2) $\int \frac{4}{x^2-4}\, dx = \int \frac{1}{x-2}-\frac{1}{x+2} \, dx = \ln |x-2|-\ln |x+2|+C$
3) Delvis integrasjon gir at $\int \sin x \cos^3 x\,dx = -\cos^4 x - 3\int \sin x \cos^3 x \,dx $. Samler vi integralene får vi at $\int \sin x \cos^3 x\,dx = -\frac14 \cos^4 x + C$
c)
\begin{align*} S_1& =1 & \\ S_2& = S_1+3 &=&4 \\ S_3 &= S_2+5 &=& 9 \\ S_4 & = S_3 + 7&=&16 \\ & \vdots \\ S_n &= \frac{n(2n-1+1)}{2}&=&n^2 \end{align*}
d)
\begin{align*} S_1 &= 1 \\ S_2 &= 2^3 \\ S_3 &= 3^3 \\ S_4 &= 4^3 \\ &\vdots \\ S_{100} & = 100^3 \end{align*}
e)
1) Amplituden er $\frac{5-1}{2}=2$. Perioden er avstanden mellom to påfølgende bunnpunkt, omtrent $2\pi$. Likevektslinja er $y=3$.
2) Sammenlignet mellom uttrykket for $f(x)$ er $a=2$ og $d=3$. Setter vi $x=0$ må vi ha at $2\sin \varphi + 3 = 4.6$, som gir at $\varphi \approx 0.93$. Siden perioden er $2\pi$ må vi ha at $f(x)=f(x+2\pi)$ for alle $x$, så $c=1$. Funksjonen blir altså $f(x)=2\sin (x+0.93)+3$.
f)
Diff.ligningen er separabel så $\int_2^{y(t)} \frac{dy}{3y+5}=\int_0^t dt$. Altså er $ \ln (3y+5)-\ln 11 = 3t$. Vi får at $3y+5=11e^{3t}$, så løsningen på initialverdiproblemet blir $y(t)=\frac{11}{3}e^{3t}-\frac53$. Setter vi inn dette i den opprinnelige ligningen ser vi at løsningen stemmer.
g)
1) $\vec{AB}=[1,1,2]$ og $\vec{AC}=[6,3,4]$, og $\vec{AC}\times \vec{AC} = [-2,8,-3]$.
2) $[-2,8,-3]\cdot [1,1,2] = -2+8-6=0$ og $[-2,8,-3]\cdot [6,3,4]=-12+24-12 = 0$, så vektorene står normal på hverandre.