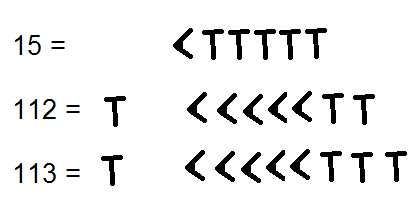2P 2012 høst ny LØSNING

Oppgave 1

4, 5, 6, 8, 10, 10, 12, 12, 12, 15, 18, 20

Median: Gjennomsnitt av tall nr. 6 og 7 : 11

Typetall: den størrelsen som opptrer flest ganger 12

Gjennomsnitt: $\frac{4+5+6+8+10+10+12+12+12+15+18+20}{12}=11$

Variasjonsbredde: 20 - 4 = 16

Oppgave 2

a) Seks år fram i tid: V(6) = $100.000\cdot 0,{85}^t=100.000\cdot 0,{85}^6$

b) For seks år siden: V(6) =$\frac{100.000}{0,{85}^t}=100.000\cdot 0,{85}^{-t}=100.000\cdot 0,{85}^{-6}$

Oppgave 3

$0,0003\cdot 0,00000015=3,0\cdot {10}^{-3}\cdot 1,5\cdot {10}^{-7}=4,5\cdot {10}^{-11}$

Oppgave 4

$\frac{(a^3{)}^{-2}\cdot a^5}{a^{-3}{\cdot }^0}=a^{-6+5-(-3)+0}=a^2$

Oppgave 5

a) $(2^3{)}^2\cdot 2^0=2^6=64$

b) $(\frac{1}{3^{-2}}{)}^2=\frac{1}{3^{-4}}=3^4=81$

Oppgave 6

$$\begin{gathered} {10}_{10}={101}_3={11}_9 \\ {100}_{10}={10201}_3={121}_9 \\ {200}_{10}={21102}_3={942}_9 \end{gathered}$$

Oppgave 7

Median. Vi sier at medianeleven er elev nr 5, altså den nest siste i interval nr. to. Får da $50+\frac{4}{5}\cdot 50\approx 90$kr

Gjennomsnitte: antar at elevene fordeler seg jevnt i intervallene: $\frac{1\cdot 25+5\cdot 75+1\cdot 125+3\cdot 175}{10}\approx 105$kr

Oppgave 8

Oppgave 9

a)

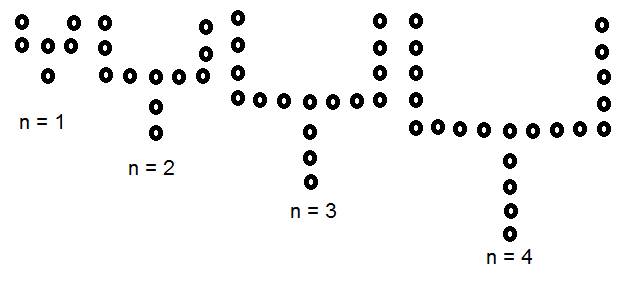
Ved opptelling ser man at figur <Math>f_5= 26</Math> og <Math>f_6= 31</Math>

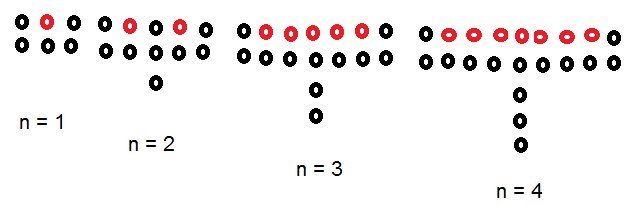
b)

Flytter noen av perlene slik at man danner et rektangel med høyde to perler og bredde (2n+1) perle. Resten av perler som ikke får plass i rektangelet blir n-1. Man får: Antall = (2n+1)2 + (n-1) = 5n + 1.

<Math>f_{36} = 5 \cdot 36 + 1 = 181</Math>

c)

5n +1 = 1000 gir n = 199

Oppgave 1

a)

Pris per kg epler: <Math>\frac{(290-210)kr}{(7-3)kg}= \frac{80kr}{4kg} = 20kr/kg</Math>

Pris for korg: <Math>210kr - 3 \cdot 20kr = 210kr - 60 kr = 150kr</Math>

b)

P = 20x + 150

c)

P = 320

320 = 20x + 150

20x = 170

x = 8,5

Hun kjøpe en korg med 8,5 kilogram epler i.

Oppgave 2

a)

<Math>2\cdot60^2 + 30 \cdot 60^1 + 11 \cdot 60^0 = \ 7200 + 1800 + 11 = 9011</Math>

b)

<Math>\sqrt{113^2 - 112^2} = 15</Math>

Oppgave 3

a)

b)

c)

Varians er et mål på spredning. Når den blir mindre er spredningen i verdiene mindre. Det er naturlig at det er tettere fra 20- 40, da det vil være mange som ligger i gruppen like bak de aller beste.

Oppgave 5

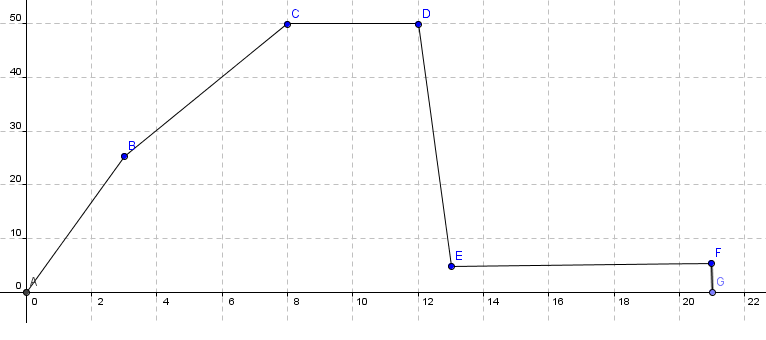
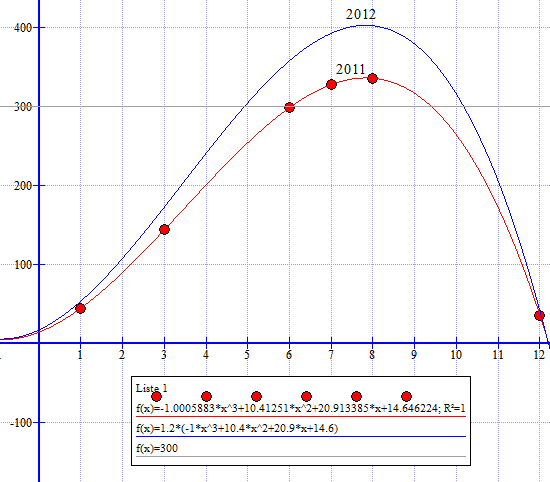
a) Se figur. x- aksen viser årets tolv måneder og y- aksen antall kilogram pølser solgt.

b) Se figur. Modellen er gitt ved <Math>f(x)=-x^3+10,4x^2+20,9x+14,6</Math>

c) En økning på 20% i 2012 tilsvarer å multiplisere modellen i b med 1,2. Man får da den blå kurven. Man ser at pølsesalget ligger over 300kg i perioden mai til oktober.

Oppgave 7

a)

$1+2^2+3^2+..+n^2$

Formelen er riktig fordi dersom høyden av stabelen er n bokser vil grunnflaten i pyramiden være n ganger n. Laget nummer to vil ha grunnflane (n-1) ganger (n-1) osv.

b)

$$\begin{gathered} 1+2^2+3^2+4^2+5^2+6^2=1+4+9+16+25+36=91 \\ {P}_n=\frac{n(n+1)(2n+1)}{n}\Rightarrow P_6=\frac{6(6+1)(2\cdot 6+1)}{6}=7\cdot 13=91 \end{gathered}$$

c)

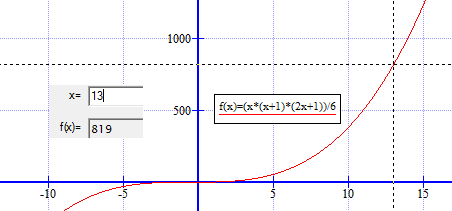
Oppgaven kan løses grafisk ved hjelp av et graf-tegneprogram, her Graph.

Man ser at med tusen bokser får man 13 høyder og bruker 119 bokser. Vi har da 181 bokser igjen. (mangler bare 15 bokser på å kunne lage en høyde til).