1T 2016 vår LØSNING

Diskusjon av denne oppgaven

Mer diskusjon av denne oppgaven

Løsning av denne oppgaven laget av mattepratbruker LektorH

DEL EN

Oppgave 1

$\frac{1,8\cdot {10}^{12}}{0,0005}=\frac{18\cdot {10}^{11}}{5\cdot {10}^{-4}}=3,6\cdot {10}^{15}$

Oppgave 2

$$\begin{gathered} (1)4^{-1}=\frac{1}{4}=0,25=F \\ (2)4\cdot (\frac{1}{4}{)}^0=4\cdot 1=4=L \\ (3)lg0,001=lg{10}^{-3}=-3=B \\ (4)5^{\frac{1}{2}}=\sqrt{5}=I \\ (5)tan{45}^{\circ }=1=G \\ (6)\sqrt[3]{27}=\sqrt[3]{3\cdot 3\cdot 3}=3=K \end{gathered}$$

Oppgave 3

$\left[\begin{array}{r}{x}^2+y^2=2x+3\\ -x+y=1\end{array}\right]$

$\left[\begin{array}{r}{x}^2+y^2=2x+3\\ y=x+1\end{array}\right]$

Setter likning 2 inn i likning en og får:

$$\begin{gathered} x^2+(x+1{)}^2=2x+3 \\ {x}^2+(x^2+2x+1)-2x-3=0 \\ 2x^2-2=0 \\ 2(x+1)(x-1)=0 \\ x=-1\vee x=1 \end{gathered}$$

Setter inn disse x verdiene i den enkleste likningen (likning to) for å finne tilhørende y verdier.

x = -1: y = x + 1 = -1 + 1 = 0

x = 1: y = x + 1 = 1 + 1 = 2

Løsning ( - 1, 0) og (1, 2).

Oppgave 4

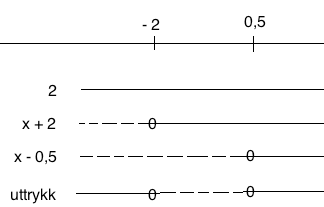
$$\begin{gathered} 2x^2+3x>2 \\ 2x^2+3x-2>0 \\ 2(x+2)(x-\frac{1}{2})>0 \end{gathered}$$

Fortegnsskjema:

$x\in <\leftarrow ,-2>\cup <\frac{1}{2},\to >$

Oppgave 5

a)

$(\sqrt{6}-\sqrt{3})\cdot (\sqrt{6}+\sqrt{3})=6-3=3$

(Tredje kvadratsetning.)

b)

$$\begin{gathered} \sqrt{45}+\sqrt{20}-\sqrt{10}-\sqrt{10}\cdot \sqrt{8}= \\ 3\sqrt{5}+2\sqrt{5}-\sqrt{80}= \\ 5\sqrt{5}-4\sqrt{5}= \\ \sqrt{5} \end{gathered}$$

Oppgave 6

$\frac{x^2+10x+25}{2x^2-50}=\frac{(x+5)(x+5)}{2(x+5)(x-5)}=\frac{x+5}{2(x-5)}$

Oppgave 7

$$\begin{gathered} 2lgx+8=2-lgx \\ 2lgx+lgx=2-8 \\ 3lgx=-6 \\ lgx=-2 \\ {10}^{lgx}={10}^{-2} \\ x={10}^{-2}=0,01 \end{gathered}$$

Oppgave 8

$$\begin{gathered} \frac{x}{4x+8}+\frac{1}{12}-\frac{4x+5}{6x+12}= \\ \frac{x}{2\cdot 2(x+2)}+\frac{1}{2\cdot 2\cdot 3}-\frac{4x+5}{2\cdot 3(x+2)}= \\ \frac{3x}{12(x+2)}+\frac{(x-2)}{12(x-2)}-\frac{2(4x+5)}{12(x-2)}= \\ \frac{3x+x+2-8x-10}{12(x+2)}= \\ \frac{-4(x+2)}{12(x+2)}=-\frac{1}{3} \end{gathered}$$

Oppgave 9

a)

P(3 blå) = $\frac{6}{10}\cdot \frac{5}{9}\cdot \frac{4}{8}=\frac{1}{6}$

b)

Dersom han ikke tar minst en rosa tar han bare blå. Den sannsynligheten kjenner vi fra a. Sannsynligheten for minst en rosa blir da:

P( minst en rosa) = 1 - P( 3 blå) = $\frac{5}{6}$

c)

Den rosa ballongen kan trekkes på tre måter, første, andre eller tredje gang:

P( en rosa og to blå) = $3\cdot \frac{4}{10}\cdot \frac{6}{9}\cdot \frac{5}{8}=3\cdot \frac{1}{6}=\frac{1}{2}$, altså 50%.

Oppgave 10

Vi observerer at graf A er den eneste som har et minimum for en negativ x verdi. 2x + 6 = 0 gir løsning for x = - 3, altså er

h(x) funksjonen til graf A.

Graf B har ingen nullpunkter : $b^2-4ac<0$

Vi observerer at $x^2-2x+9=0$ ikke har noen løsning, altså er

f(x) funksjonen til graf B.

g(x) er da funksjonen til C.

Oppgave 11

a)

$$\begin{gathered} f´(x)=3x^2-10x+3 \\ f´(2)=3\cdot 4-10\cdot 2+3=-5 \end{gathered}$$

b)

$$\begin{gathered} f(1)=1-5+3+4=3 \\ f(3)=27-45+9+4=-5 \end{gathered}$$

$\frac{\mathrm{\Delta }y}{\mathrm{\Delta }x}=\frac{-5-3}{3-1}=-4$

Oppgave 12

a)

BC = 10

Høyde i grå trekant: $$\begin{gathered} h^2=100-25 \\ h=\sqrt{75}=5\sqrt{3} \end{gathered}$$

Areal: $A=\frac{Gh}{2}=\frac{10\cdot 5\sqrt{3}}{2}=25\sqrt{3}$

b)

Areal av grønn og blå trekant:

$$\begin{gathered} A=\frac{6\cdot \sqrt{6^2-3^2}}{2}+\frac{8\cdot \sqrt{8^2-4^2}}{2}=3\sqrt{27}+4\sqrt{48}= \\ 3\sqrt{9\cdot 3}+4\sqrt{16\cdot 3}=9\sqrt{3}+16\sqrt{3}=25\sqrt{3} \end{gathered}$$

Altså samme svar som i a.

Oppgave 13

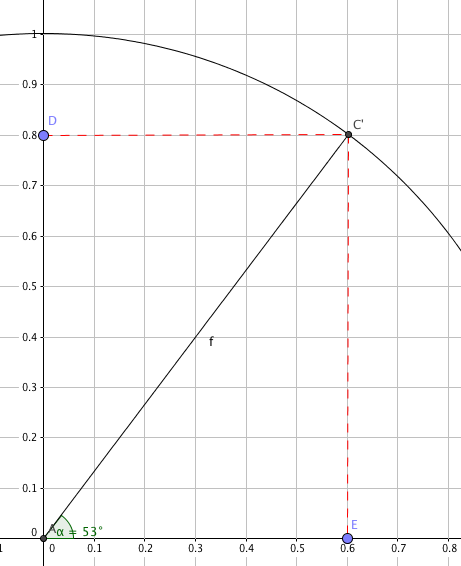
Vi leser av figuren:

$$\begin{gathered} cos{53}^{\circ }\approx 0,6 \\ sin{53}^{\circ }\approx 0,8 \end{gathered}$$

Tangens:

$tan{53}^{\circ }\approx \frac{8}{6}\approx 1,33$

Oppgave 14

a)

Funksjonen har ekstremalpunkter når den deriverte er null. For x = 0 og x = 4 er det tilfelle. x = 0 er et toppunkt fordi den deriverte skifter fra positiv til negativ verdi, og x = 4 er et bunnpunkt fordi den deriverte skifter fra negativ til positiv verdi.

b)

Likningen for en rett linje er y = ax + b

I punktet (2,-3) er den deriverte lik -2. Det gir y= -2x + b

Setter så punktet (2, -3) inn for x og y for å finne b: $-3=-2\cdot 2+b$ som gir b=1.

Likningen blir da:

y = -2x + 1

Oppgave 1

a)

Definerer g(x)=f(x) siden jeg gav den feil navn i Geogebra:

b)

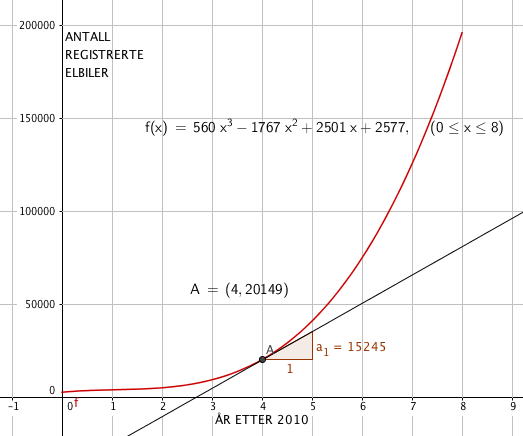
f(4)= 20149, Fra figuren i a. Det betyr at i 2014 var det ca 20150 registrerte elbiler.

f´(4) = 15245 betyr at økningen i registrerte elbiler i 2014 var ca. 15245.

Oppgave 2

a)

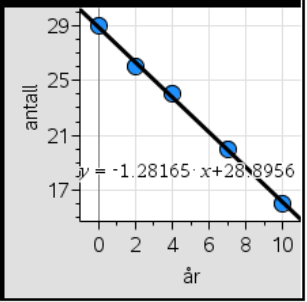
En brukbar modell er f(x)= - 1,3x + 31,5

b)

Modeller tar utgangspunkt i at et gitt antall personer, det samme hvert år, slutter å røyke. I følge modellen vil det derfor ikke være røykere i 2025. Dette er lite trolig. Konklusjonen er at modellen ikke kan brukes i utviklingen mot 2025. En eksponentiell modell ville trolig være bedre.

Oppgave 3

a)

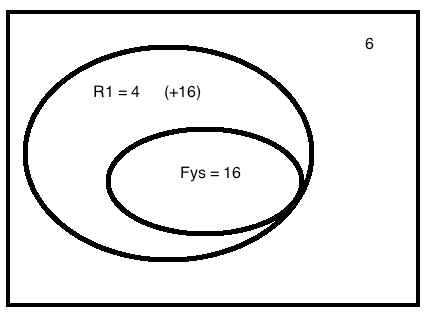
	R1	ikke R1	Total
Fysikk	16	0	16
Ikke Fysikk	4	6	10
Total	20	6	26

b)

Det er fire elever som har R1 og ikke fysikk:

$P(R1\cap \overline{fysikk})=\frac{4}{26}=\frac{2}{13}$

c)

Alle elever som har valgt fysikk har også valg R1. Sannsynligheten er 1.

Oppgave 4

a)

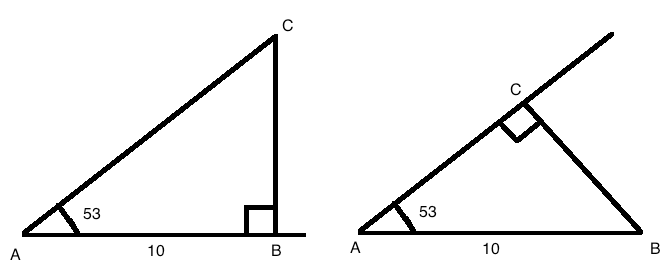
Den rette vinkelen kan ligge i B, eller den kan ligge i C.

b)

BC dersom vinkel B er 90 grader: $$\begin{gathered} tan53=\frac{BC}{10} \\ BC=10\cdot tan53=13,3\approx 13 \end{gathered}$$

BC dersom vinkel C er 90 grader: $$\begin{gathered} sin53=\frac{BC}{10} \\ BC=10\cdot sin53\approx 8 \end{gathered}$$

Oppgave 5

$$\begin{gathered} f(x)=x^3+b{x}^2+cx+d \\ f´(x)=3x^2+2bx+c \end{gathered}$$

Nullpunkt for x=4 gir oss likningen: $4^3+16b+4c+d=0$

Minimumspunkt i (3,-5) gir oss to likninger; f(3)= -5 og f´(3) =0:

$$\begin{gathered} 3^3+b{3}^2+3c+d=-5 \\ 3\cdot 3^2+6b+c=0 \end{gathered}$$

Da har vi tre likninger med tre ukjente, bruker cas i Geogebra og får:

$$\begin{gathered} b=-5,c=3,d=4 \\ f(x)=x^3-5x^2+3x+4 \end{gathered}$$

Oppgave 6

Areal av begge kvadrater: $A=x^2+y^2$

Omkrets av begge: $4x+4y=16$ som gir $x=4-y$

Innsatt i areal:

$$\begin{gathered} A(y)=(4-y{)}^2+y^2=2y^2-8y+16 \\ A´(y)=4y-8 \\ A´(y)=0\Rightarrow y=2 \end{gathered}$$

Det betyr, fra omkretslikningen, at x også er lik 2.

Arealet av kvadratene blir minst når x = y = 2.

Oppgave 7

Firkanten ABCD består av to trekanter der arealet implisitt er gitt.

Bruker først CAS i Geogebra til å finne AD, ved hjelp av cosinussetningen:

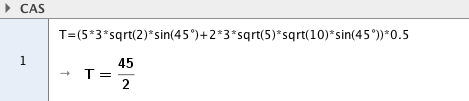
Ser bort fra den negative verdien. Bruker så arealsetningen på hver av trekanten og får:

Arealet av firkanten er $\frac{45}{2}$.