R1 2016 høst LØSNING

Løsning laget av mattepratbruker DennisChristensen

Diskusjon av og delvis løsning på denne oppgaven

Oppgave 1

a)

$$\begin{gathered} f(x)=2x^2-5x-6 \\ {f}^{\prime }(x)=4x-5 \end{gathered}$$

b)

$$\begin{gathered} g(x)=xlnx \\ {g}^{\prime }(x)=lnx+x\cdot \frac{1}{x}=lnx+1 \end{gathered}$$

c)

$$\begin{gathered} h(x)=\frac{e^{2x}}{x-3} \\ {h}^{\prime }(x)=\frac{2e^{2x}(x-3)-e^{2x}}{(x-3{)}^2}=\frac{(2x+7)e^{2x}}{(x-3{)}^2} \end{gathered}$$

Oppgave 2

a)

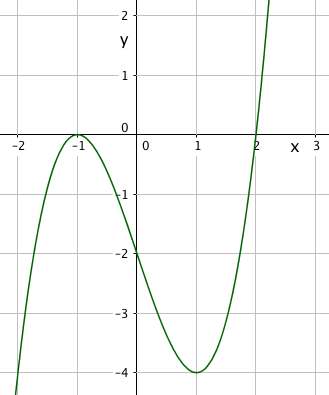
$$\begin{gathered} f(x)=0 \\ (x+1{)}^2(x-2) \\ x=-1\vee x=2 \end{gathered}$$

Nullpunkter: (-1, 0) og (2, 0)

b)

$$\begin{gathered} f^{\prime }(x)=0 \\ {f}^{\prime }(x)=2(x+1)(x-2)+ \end{gathered}$$

c)

Oppgave 3

a)

$$\begin{gathered} \frac{2x+10}{x^2-25}+\frac{x}{x+5}-\frac{4}{2x-10}= \\ \frac{2x+10}{(x+5)(x-5)}+\frac{x}{x+5}-\frac{4}{2(x-5)}= \\ \frac{4x+20+2x(x-5)-4(x+5)}{2(x+5)(x-5)}= \\ \frac{2x(x-5)}{2(x+5)(x-5)}= \\ \frac{x}{x+5} \end{gathered}$$

b)

$$\begin{gathered} \frac{2x+10}{x^2-25}+\frac{x}{x+5}=\frac{4}{2x-10} \\ 2(2x+10)+2x(x-5)=4(x+5) \\ 4x+20+2x^2-10x=4x+202x^2-10x=0 \\ x=0\vee 2x-10=0 \\ x=0\vee x=5 \end{gathered}$$

Må forkaste x = 5, da det gir null i nevner.

L={ 0 }

En mere elegant og tidsbesparende løsning er å løse svaret fra a lik null:

$\frac{x}{x+5}=0$

som gir x=0 direkte.

Oppgave 4

a)

$$\begin{gathered} 2^{3x-2}-13=3 \\ {2}^{3x-2}=2^4 \\ 3x-2=4 \\ 3x=6 \\ x=3 \end{gathered}$$

b)

$$\begin{gathered} (lgx{)}^2+lgx-2=0 \\ u=lgx \\ {u}^2+u-2=0 \\ ABC-formel \\ u=-2\vee u=1 \\ lgx=-2\vee lgx=1 \\ x=0,01\vee x=10 \end{gathered}$$

Oppgave 7

a)

$\mathrm{△}PCB$ er likebeint, derfor er $\mathrm{\angle }PCB=v$

$\mathrm{\angle }PCE$ er 90 grader fordi toppunktet ligger på pereferien og den spenner over 180 grader av sirkelsektoren.

$\mathrm{\angle }ABC$ er også 90 grader, derfor må $\mathrm{\angle }ACE=v.$

$\mathrm{\angle }A$ er felles i begge tekantene og $\mathrm{\angle }ACE=\mathrm{\angle }PCB=v$, derfor er trekantene formlike.

b)

$$\begin{gathered} AB=c,EB=a \\ AE=AB-EB=c-a \\ BP=a,AB=c \\ AP=AB+BP=c+a \end{gathered}$$

c)

Forholdet mellom sammsvarende sider i formlike trekanter er likt.

$$\begin{gathered} \frac{AP}{AC}=\frac{AC}{AE} \\ \frac{c+a}{b}=\frac{b}{c-a} \end{gathered}$$

d)

$$\begin{gathered} \frac{c+a}{b}=\frac{b}{c-a} \\ (c+a)=\frac{b^2}{c-a} \\ (c+a)(c-a)=b^2 \\ {c}^2-ab+ab-a^2=b^2 \\ {a}^2+b^2=c^2 \end{gathered}$$

Oppgave 8

(ii) er grafen til funksjonen. Den har minimumspunkt for x=0 og vender sin hule side opp hele tiden, dvs. ingen vendepunkter.

(i) er grafen til f'(x). Den er null oiorogo når f(x) har et minimum. (iii) er grafen til den dobbeltderiverte.