2P 2017 vår LØSNING

Løsning bidratt av Lektor Ørjan Augedal, Fana privat gymnas

Diskusjon av denne oppgaven

Oppgave 1

0,0,0,0,0,1,1,1,1,1,1,2,2,3,3,4

Variasjonsbredde: 4 -0 =4 ( største minus minste)

Typetall: 1 (den det er mest av)

Median 1 ( den i midten når materialet er organisert stigende)

Gjennomsnitt; Sum søsken delt påantall elever: $\frac{20}{16}=\frac{5}{4}=1,25$

Oppgave 2

$\frac{25}{125}=\frac{1}{5}=20$

20% tok bussen den dagen.

Oppgave 3

$$\begin{gathered} 5^0\cdot 2^3\cdot 8^{-2}\cdot (4^{-1}{)}^{-3} \\ =1\cdot 8\cdot \frac{1}{64}\cdot 4^3 \\ =8 \end{gathered}$$

Oppgave 4

I 10 liter vann, som er det samme som 100 dL vann er det ca. $3,0\cdot {10}^{25}$

For å finne antall molekyler i 1,5 dL, deler vi på 100 og ganger med 1,5:

$3,0\cdot {10}^{25}\cdot \frac{1,5}{100}=4,5\cdot {10}^{23}$

Oppgave 5

a)

Dersom noe vokser periodisk med en fast størrelse har man en lineær sammenheng:

$f(x)=80000x+1200000$

b)

Dersom noe vokser periodisk med en fast prosent er veksten eksponentiell. Vekstfaktoren her er 1,08:

$g(x)=1200000\cdot 1,{08}^x$

c)

B er rettlinjet og KAN beskrive f.

A later til å være eksponentiell og KAN beskrive g.

Både A og C vokser, men ved eksponentiell positiv vekst vil den momentane veksten øke med tiden. Det er tillfelle i A. I graf C avtar den.

Oppgave 7

b)

Vi setter figurnummer lik n.

Figur en har en mere enn det dobbelte av figurnummeret: 1 pluss 2 ganger 1.

Figur 2: 1pluss 2 ganger 2.

Figur 5: 1 pluss 2 ganger 5.

Figur n: 2n+1.

c)

Omkretsen er hele tiden to mere enn figurnummeret. Altså n+2.

d)

Finner antall pinner i omkretsen ved å dele på 2,5.

104 : 2,5 =42 pinner

Fra oppgave c ser man at det er snakk om figur nr. 40. Fra oppgave b finner man antall pinner totalt til å være 2n+1 = 81 pinner.

Oppgave 1

a)

b)

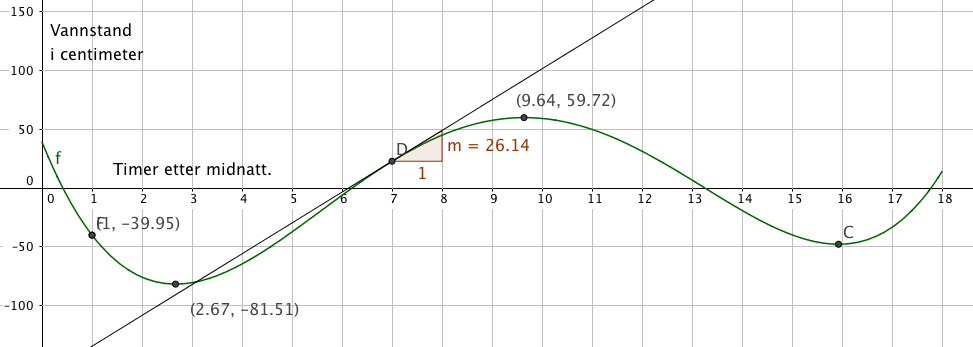
Vi ser ar f(1) er ca. - 40 cm (markert) og at f(12) er ca. 31 cm (ikke markert), fra fuguren i a.

c)

Fra Figuren i a ser man at den største forskjellen er 59,72+ 81,51 = 141,23 cm. Altså ca. 141 cm i fieskjell.

Oppgave 5

a)

Vi vet at søylehøyde er frekvens delt på klassebredde. Søylehøyden leser vi av i figuren. Vi har tre søyler og får:

$$