Løsning del 2 utrinn Vår 18

a)

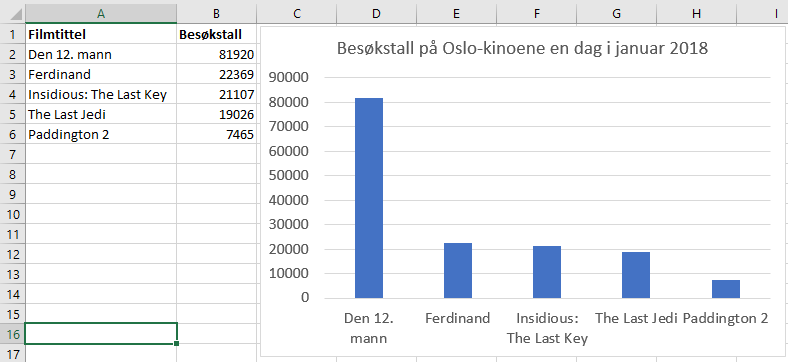
Brukte Excel til å lage et stolpediagram. Et sektordiagram ville også passet.

b)

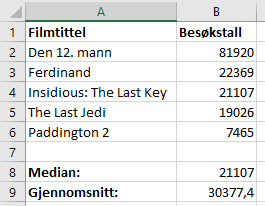
Bruker Excel til å finne median og gjennomsnitt:

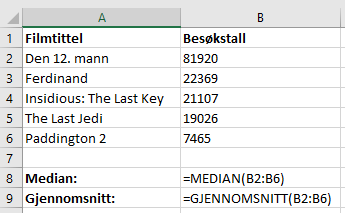
Med formler:

Medianen er 21107 besøkende. Gjennomsnittet er 30377,4 besøkende.

c)

Det var mange flere besøkende på filmen "Den 12. mann" enn på de andre filmene. Dette besøkstallet drar derfor opp gjennomsnittet. De fire andre filmene hadde ganske like besøkstall, så medianen er derfor mye lavere enn gjennomsnittet.

a)

Det er 4 km fra roklubben til øya. Dette ser man på y-aksen.

b)

Hele turen tok 100 minutter, det vil si 1 timer og 40 minutter (siden 1 time = 60 minutter). Dette ser man på x-aksen.

Klokken var 10.30 da de startet turen og turen varte i 1 time og 40 minutter, så klokken var 12.10 da de som tilbake til roklubben.

c)

Avstanden fra øya til roklubben er 4 km (se oppgave a).

Tiden de brukte fra øya til rokluben er 100 min - 60 min = 40 min. Dette ser man på x-aksen.

Gjør om 40 minutter til timer: $\frac{40min}{60min/t}=\frac{2}{3}t$

Gjennomsnittsfarten $v$ er strekning delt på tid.

$v=\frac{4km}{\frac{2}{3}t}=6km/t$

Gjennomsnittsfarten til Eva og Peter fra øya til roklubben er 6 km/t.

a)

Sum til fullpris er $899+298=1197$ kroner

20% av 1197 er: $\frac{20\cdot 1197}{100}=239,40$ kroner.

Trekker det fra fullpris og får 1197 kr. - 239,40 kr = 957,60 kroner.

Han må betale kr 958 etter rabatten.

Dersom man får 20% rabatt betaler man 80% av prisen. Det er det samme som å gange 0,8 med den fulle prisen:

Rabbatert pris: $0,8(899kr+298kr)=957,60$

b)

$P(X=2)=0,90\cdot 0,90=0,81$

Sannsynligheten for at Adam scorer på to straffekast etter hverandre er 0,81, det vil si 81%.

c)

Formel for volum av en kule er: $V=\frac{4}{3}\pi r^3$

Formel for omkrets av en sirkel er: $O=2\pi r$. Dermed er $r=\frac{O}{2\pi }$.

Radius til basketballen er: $r=\frac{74,5cm}{2\pi }=11,86cm$

Volumet av basketballen er: $V=\frac{4}{3}\pi (11,86cm{)}^3=6987,8c{m}^3\approx 7000c{m}^3=7L$

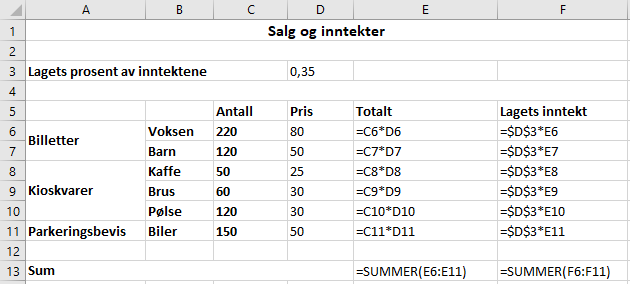
Oppgave 4

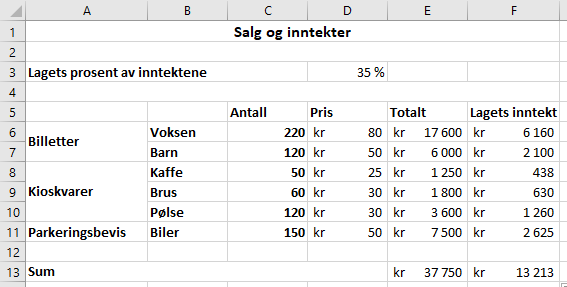
Bruker Excel.

Med formler:

a)

b)

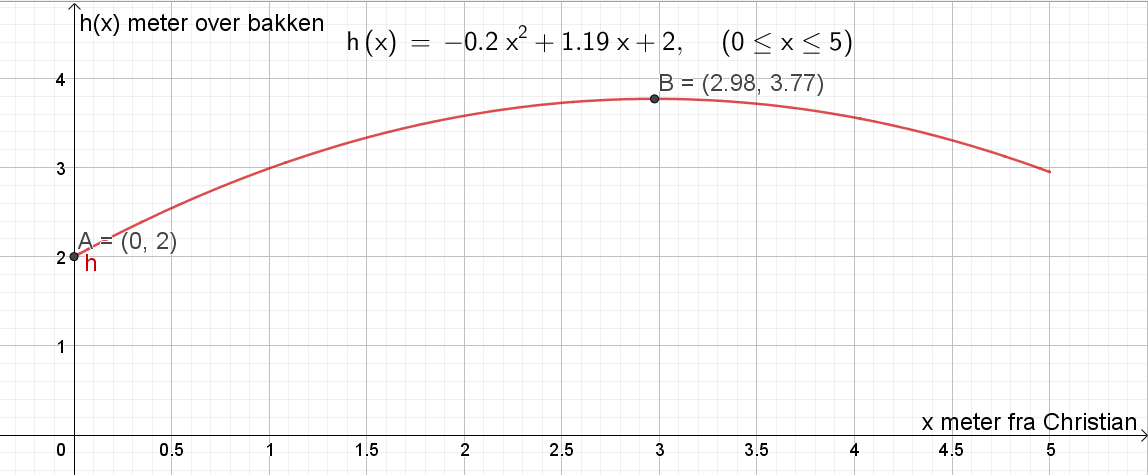
Basketballen er 2 meter over bakken idet den forlater hånden til Christian. Se punkt A på figuren i oppgave a). Kommando: Skjæring mellom to objekt mellom grafen til $h$ og y-aksen.

c)

Basketballen er 3,77 meter over bakken i det høyeste punktet. Se punkt B på figuren i oppgave a). Kommando: Ekstremalpunkt[h].

a)

Det er 60 sekunder i ett minutt.

$\frac{60s}{15s}=4$.

15 sekunder går altså opp 4 ganger i 60 sekunder.

Daniella har derfor $20\cdot 4=80$ pulsslag i løpet av 1 minutt.

b)

$$\begin{gathered} M=211-0,64\cdot A \\ M=211-0,64\cdot 25=195 \end{gathered}$$

Makspulsen til Monica er 195 slag i minuttet.

c)

$$\begin{gathered} M=211-0,64\cdot A \\ 0,64\cdot A=211-M \\ A=\frac{211-M}{0,64} \end{gathered}$$

Det er det samme som $A=\frac{M-211}{-0,64}$. Skulle du regne deg frem til det svaret, er det også riktig.

a)

b)

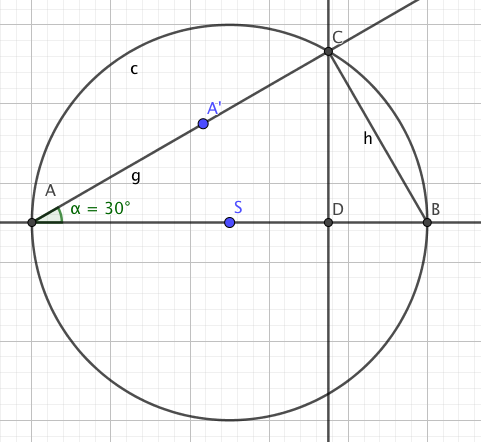
Begge trekantene har en vinkel på 90 grader i D. Vinkel ACD er 60, fordi vinkel A er 30 grader. Siden vinkel ACB er 90 og ACD 60 grader må vinkel DCB være 30 grader.

Trekantene er derfor formlike.

c)

For å finne CD kan vi gå veien om arealet av trekanten.

Vet at CB = 5 cm og at $AC=\sqrt{100-25}=8,66$

Arealet av trekanten ABC blir da $A=\frac{5\cdot 8,66}{2}=21,65c{m}^2$

CD er høyden i ABC, der grunnlinjen er 10cm: $A=\frac{gh}{2}\Rightarrow h=\frac{2A}{g}\Rightarrow CD=\frac{2\cdot 21,65}{10}=4,3$

CD er 4,3 cm.

Alternativt kan man bruke formlikhet. Vi vet at trekant ABC er forlik med trekant BCD. Siden alle sider i BCD er halvparten av sidene i ABC, blir CD halvparten av AC (som er tilsvarende side i trekant ABC), altså 8,66 cm : 2 = 4,3 cm.

a)

Vi observerer at det er tre sirkelsektorer av ${240}^{\circ }$ og tre av ${120}^{\circ }$, alle med radius 1,5 cm. Det gir tre sirkler med radius 1,5 cm. Omkretsen av disse er:

$O=3\cdot 2\pi \cdot 1,5cm=9\pi$ cm.

b)

Vi vet at avstanden SB er 3 cm og avstanden SD er 1,5 cm. Finner DB ved Pytagoras og ganger svaret med seks fordi DB er halvparten av en side i en likesidet trekant.

$$\begin{gathered} (DB{)}^2=3^2-1,5^2 \\ DB=2,6 \\ {O}_{ABC}=6\cdot 2,6=15,6cm \end{gathered}$$

a)

Vi observerer at summen av første og siste tall er den samme som summen av andre og nest siste osv. Vi ser også at antall tall er partall.

For n= 1000 blir det 500 par av sum 1001 som gir $S_{1000}=500\cdot 1001=500500$

b)

Fra a ser man om man deler n på 2 og ganger med (1+n) så får vi summen.

$S_n=\frac{n}{2}(1+n)$