1P 2018 vår LØSNING

Diskusjon av oppgaven på matteprat

Oppgaven som pdf

Løsningsforslag laget av LektorNilsen

DEL EN

a)

4,2% - 5,6 % = -1,4%

De gikk tilbake med 1,4 prosentpoeng.

b)

De hadde 5,6 prosentpoeng. Endringen var på - 1,4 prosentpoeng.

Tilbakegang i prosent: $-\frac{1,4\cdot 100}{5,6}=-25$

Tilbakegangen var på 25%.

Oppgave 2

Vi ser at melk er begrensningen. Vi har mel nok til tre ganger original oppskrift, men bare melk nok til 2,5 ganger original oppskrift. Vi kan derfor lage 12 ganger 2,5 som er 30 boller. (Vi hadde mel nok til 36).

Oppgave 3

Forholdet mellom indeks og pris er det samme dersom prisen følger indeksen. Vi kaller prisen i 2017 for x:

$$\begin{gathered} \frac{x}{120}=\frac{1000}{80} \\ 80x=120000 \\ \frac{80x}{80}=\frac{120000}{80} \\ x=1500 \end{gathered}$$

Prisen i 2017 var 1500 kroner.

Oppgave 4

Målestokken er lengde av modell delt på lengde i virkelighet:

$\frac{9cm}{45km}=\frac{9cm}{45000m}=\frac{9cm}{4500000cm}=\frac{1}{500000}$

Finner først samme benevning i teller og nevner. Deler så teller og nevner på 9 fordi målestokk alltid oppgies som 1: "noe", i dett tilfellet 1: 500 000.

a)

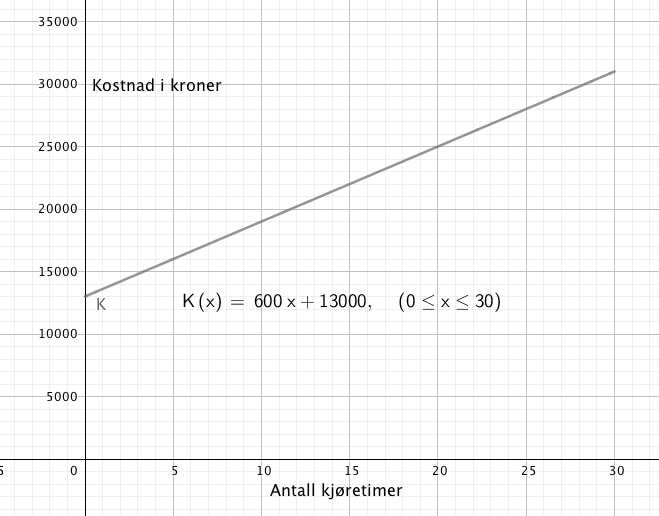
Prisen på en kjøretime er 600 kroner, men behovet for kjøretimer kan variere. Kostnadsfunksjonen blir derfor:

K(x) = 600x + 13000

x er antall kjøretimer.

b)

Grafen viser kostnaden ved å ta sertifikat når antall kjøretimer varierer mellom null og tretti.

c)

De er ikke proporsjonale på grunn av den faste utgiften på 13000 kroner.

Oppgave 6

Vi vet at prisen nå er 8000 kroner, og at den har sunket i verdi med 12% i 4 år. Vi får følgende uttrykk:

$$\begin{gathered} Nypris\cdot 0,{88}^4=8000 \\ Nypris=\frac{8000}{0,{88}^4} \end{gathered}$$

Altså er alternativ 3 riktig.

Oppgave 7

Det er totalt 36 (6x6) mulige utfall.

Det er seks muligheter (utfall) for like øyner. Sannsynligheten for like øyner blir da P(like) = $\frac{6}{36}=\frac{1}{6}$

Sum 5 eller mindre på to terninger: (1+1), (1+2), (1+ 3), (1+4), (2+1), (2+2), (2 +3), (3+1), (3+2), (4+1). Det er 10 mulige utfall for sum fem eller mindre:

$P(5ellermindre)=\frac{10}{36}=\frac{5}{18}$

Det er altså størst sannsynlighet for å få sum mindre eller lik fem.

Oppgave 8

$$\begin{gathered} O=2\pi r=d\pi \\ d=\frac{o}{\pi }=\frac{66}{\pi } \end{gathered}$$

Siden pi er større enn 3 ( 3,14) blir d mindre enn 22, så ja, mynten går ned i flasken.

a)

Høyden av en lampeskjermside:

Pytagoras

$$\begin{gathered} h^2={13}^2-5^2 \\ {h}^2=169-25 \\ {h}^2=144 \\ h=12 \end{gathered}$$

Høyden er 12 cm, arealet blir da:

$12cm\cdot 10cm+5cm\cdot 12cm=120c{m}^2+60c{m}^2=180c{m}^2$

b)

Areal av alle fire sider pluss 10% ekstra:

$180c{m}^2\cdot 4\cdot 1,1=792c{m}^2$

DEL TO

a)

b)

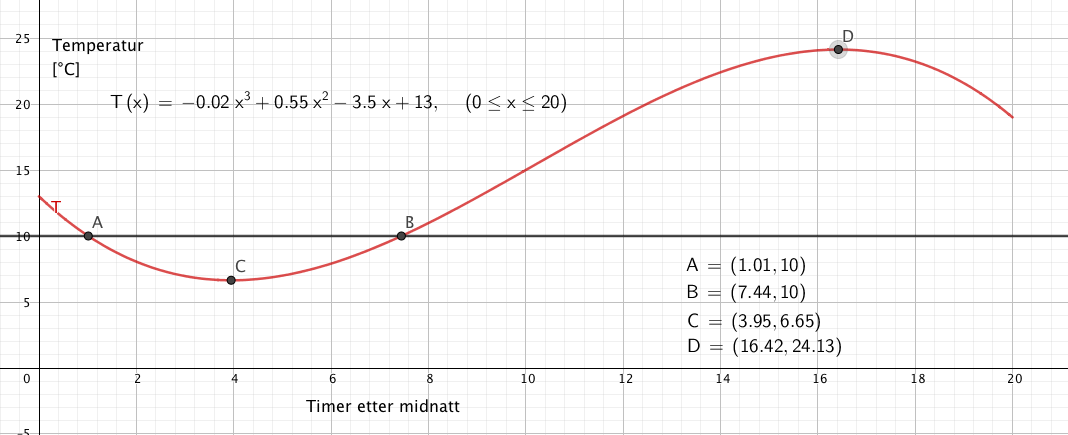
Fra figuren i a ser man at temperaturen er 10 grader ca kl 01 på natta og litt før halv åtte på morgenen.

c)

Vi finner ekstremalpunkter (topp og bunn) og trekker laveste temperatur fra høyeste, da ser vi at temperaturforskjellen er ca 17,5 grader.

a)

Hun tjener brutto: $210kr\cdot 162,5=34125kr$

Pensjonsavgift, 2%: $34125kr\cdot 0,02=682,5kr$

Skattbar inntekt: $34125kr-682,5kr=33442,5kr$

Skatt $33442,5kr\cdot 0,32=10701,60kr$

Netto inntekt: $33442,5kr-10701,60=22740,90kr$

b)

Feriepengegrunnlag:

$$\begin{gathered} 0,12\cdot x=47736kr \\ x=\frac{47736kr}{0,12}=397800kr \end{gathered}$$

a)

b)

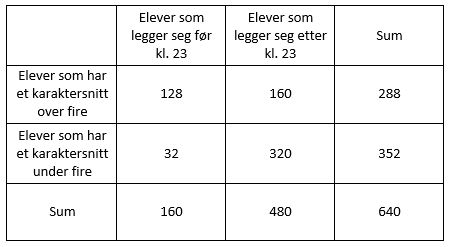
P(karaktersnitt over 4) $=\frac{288}{640}=0,45$

Sannsynligheten for at en tilfeldig valgt elev har et karaktersnitt over fire er 0,45, altså 45%.

c)

P(elev som har karaktersnitt over 4 legger seg før kl.23) $=\frac{128}{288}\approx 0,444$

Sannsynligheten for at en elev som har et karaktersnitt over fire, også legger seg før kl.23 er ca. 0,444, altså 44,4%.

a)

$△ABC\sim △FGC$

Fordi $\mathrm{\angle }$ C er felles i begge trekantene, og $\mathrm{\angle }A=\mathrm{\angle }F$. Da er vinkel B lik vinkel G og trekantene er formlike.

$△ABC\sim △BDE$

Fordi $\mathrm{\angle }A=\mathrm{\angle }E$ og vi har toppvinkler i B ( $\mathrm{\angle }DBE=\mathrm{\angle }CBA$). Da er vinkel C og D like, og trekantene er formlike.

b)

Forholdet mellom trekantene ABC og BDE er : $\frac{AB}{BE}=\frac{80}{20}=4$.

AC er er da lik 4DE, altså: $AC=4\cdot 32m=128m$

FC = AC - AF = 108m.

FG: $$\begin{gathered} \frac{128}{108}=\frac{80}{FG} \\ FG=\frac{80\cdot 108}{128}=67,5 \end{gathered}$$

FG er 67,5 meter.

c)

Arealet av ABGF er arealet av trekanten ABC minus arealet av trekanten FGC:

$A=\frac{128m\cdot 80m}{2}-\frac{108m\cdot 67,5m}{2}=5120m^2-3645m^2=1475m^2$

Volumet blir:

$V=A\cdot h=1475m^2\cdot 0,15m=221,25m^3$

Han trenger 221,25 kubikk meter til jobben.

Oppgave 5

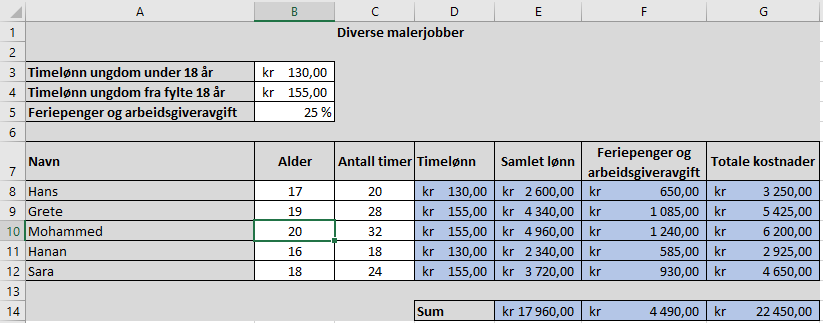
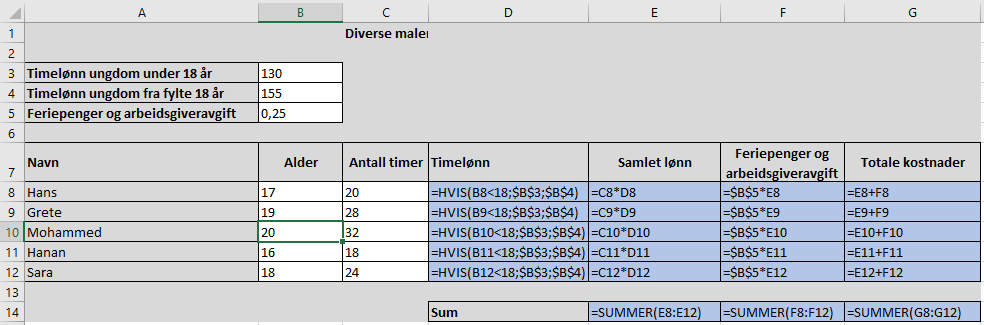
Bruker Excel. Uten formler:

Med formler:

a)

Alternativ 3 er det eneste som kun er knyttet opp mot mengde moreller plukket. ( I 2 har han også fastlønn).

Pris på kurven uten MVA er:

$$\begin{gathered} x\cdot 1,15=69 \\ x=60 \end{gathered}$$

L = lønn og x = kurver plukket. Lønnen blir da:

$L=0,12\cdot 60x=7,20x$

b)

$$\begin{gathered} 80+3x>135 \\ 3x>55 \\ x>18,33 \end{gathered}$$

Han må plukke mere enn 18 kurver per time for at alternativ 2 skal gi høyere lønn.

c)

$$\begin{gathered} L=7,20x \\ 1000=7,20x \\ x=\frac{1000}{7,20} \\ x=138,89 \end{gathered}$$

Han må plukke 139 kurver.

a)

Volum av en sylinder er gitt ved

$V=\pi \cdot r^2\cdot h$

Volum av den minste pizzaren, med radius 10 cm:

$V=\pi \cdot (10cm{)}^2\cdot 1,25cm\approx 393c{m}^3$

b)

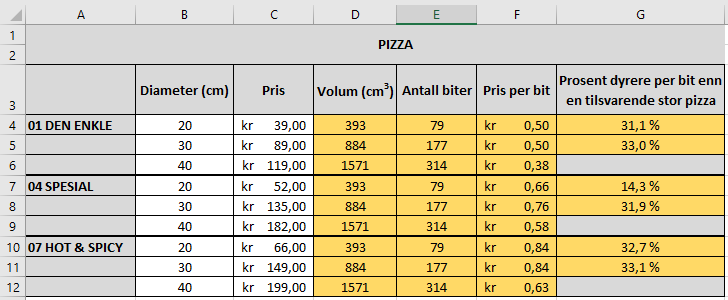
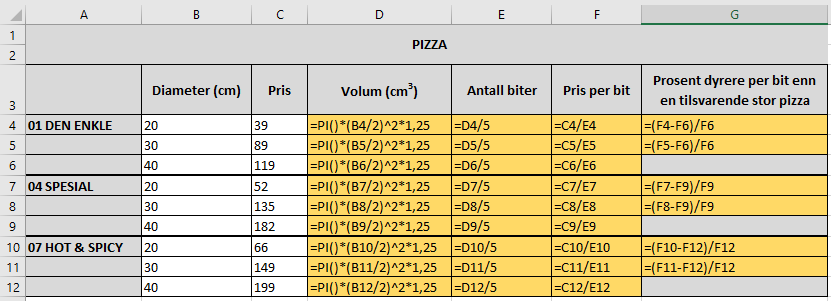
Bruker Excel. Uten formler:

Med formler: