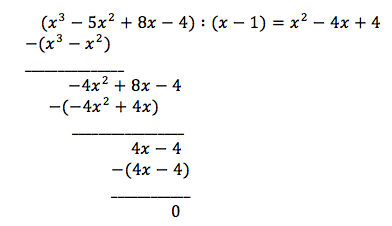S2 2018 høst LØSNING

Diskusjon av oppgaven på matteprat

DEL 1

Oppgave 1

a)

$$\begin{gathered} f(x)=e^{2x} \\ {f}^{\prime }(x)=2e^{2x} \end{gathered}$$

b)

$$\begin{gathered} g(x)=\frac{x^4-1}{x^2} \\ {g}^{\prime }(x)=\frac{4x^3\cdot x^2-(x^4-1)\cdot 2x}{(x^2{)}^2} \\ =\frac{4x^5-2x^5+2x}{x^4} \\ =\frac{2x^5+2x}{x^4} \\ =\frac{2x^4+2}{x^3} \end{gathered}$$

c)

$$\begin{gathered} h(x)=x^3\cdot lnx \\ {h}^{\prime }(x)=3x^2\cdot lnx+x^3\cdot \frac{1}{x} \\ =3x^2\cdot lnx+x^2 \end{gathered}$$

Oppgave 2

Dersom $-1<k<1$ i en geometrisk tallfølge $a_n=a_1{k}^{n-1}$ sier vi at den konvergerer.

I slike tilfeller er $\underset{n\to \mathrm{\infty }}{lim}{S}_n=\underset{n\to \mathrm{\infty }}{lim}\sum _{i=1}^n{a}_i=\frac{a_1}{1-k}$

a)

Vi har rekken $a_n=54\cdot {\frac{1}{3}}^{n-1}$. I denne rekka er $k=\frac{1}{3}$. Det vil si at rekken konvergerer. Summen er gitt ved:

$\underset{n\to \mathrm{\infty }}{lim}{S}_n=\frac{54}{1-\frac{1}{3}}=\frac{54}{\frac{2}{3}}=\frac{54\cdot 3}{2}=81$

b)

Vi har rekken $a_n=4\cdot (-2{)}^{n-1}$. I denne rekka er $k=-2$. Det vil si at rekken ikke konvergerer.

Oppgave 3

a)

x runder løpt	1	2	3	4	n
f(x) kroner tjent per runde	10	15	20	25	$F_n$
utregning for å finne formel	5*2	5*3	5*4	5*5	$5\ast (n+1)=5n+5$

Inntekten per runde $F_n$ er gitt ved $F_n=5n+5$, der x er antall runder løpt og $n>0$. Setter $F_n=100$

$$\begin{gathered} 5n+5=100 \\ n+1=20 \\ n=19 \end{gathered}$$

Lise må løpe 19 runder for å tjene 100 kroner på den siste runden.

b)

$$\begin{gathered} S=\sum _{n=1}^{25}5n+5 \\ =\frac{(5\cdot 1+5)+(5\cdot 25+5)}{2}\cdot 25 \\ =\frac{10+130}{2}\cdot 25 \\ =70\cdot 25=1750 \end{gathered}$$

Bedriften må gi totalt 1750 kroner dersom Lise løper 25 runder.

Oppgave 4

a)

Funksjonen f er delelig på (x-1), derfor er (x-1) en faktor i f(x).