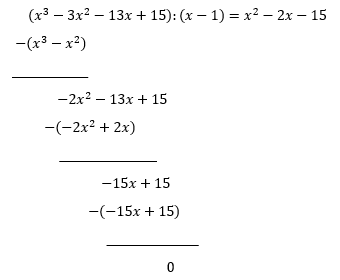S2 2018 vår LØSNING
Diskusjon av denne oppgaven på matteprat
Løsning laget av mattepratbruker Tommy O.
DEL 1
Oppgave 1
a)
$f(x)=2x^3-4x+1 \\ f'(x) = 6x^2 - 4$
b)
$g(x)=\frac{x}{e^x}$
$g'(x)= \frac{1 \cdot e^x - x \cdot e^x}{(e^x)^2} = \frac{e^x (1-x)}{(e^x)(e^x)} = \frac{1-x}{e^x} $
c)
$h(x)=ln(x^2+4x) \\ g(u)=ln(u), \quad u=x^2+4x \\ h'(x)=g'(u)\cdot u'(x)=\frac{1}{u} \cdot u' =\frac{2x+4}{x^2+4x}$
Oppgave 2
$ I \quad \, 5x+y+2z=0 \\ II \,\,\,\, 2x+3y+z=3 \\ III \, 3x+2y-z=-3$
Legger sammen likning II og III.
$2x+3x + 3y + 2y + z-z = 3 -3 \\ 5x+5y=0 \\ x+y=0 \\ x=-y$
Setter inn $x=-y$ i likning I.
$5\cdot (-y)+y+2z=0 \\ -4y+2z=0 \\ 2z=4y \\ z=2y$
Setter inn $z=2y$ og $x=-y$ i likning II.
$2\cdot (-y)+3y+2y=3 \\ 3y=3 \\ y=1$
$x=-y=-1$
$z=2y=2\cdot 1=2$
Løsning: $x=-1,\,y=1,\,z=2$
Oppgave 3
a)
$P(x)=x^3-3x^2-13x+15$
$P(1)=1^3-3\cdot 1^2-13\cdot 1+15= 1-3-13+15=0$
x=1 er et nullpunkt, så P(x) er delelig med (x-1).
b)
Utfører polynomdivisjon for å faktorisere P(x)
Resten faktoriseres: $x^2-2x-15=(x^2-5x+3x+(-5)\cdot 3)=(x-5)(x+3)$. Bruk andregradsformelen ved behov.
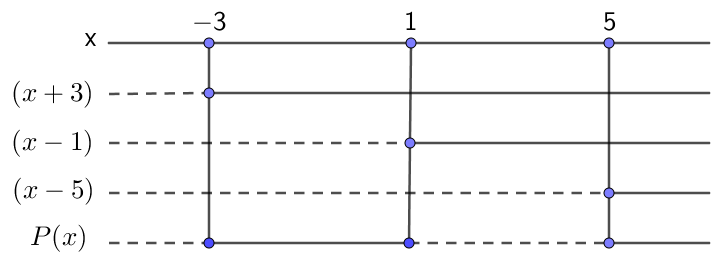
Vi har $P(x)=(x-5)(x-1)(x+3)$. Bruker fortegnsskjema for å løse ulikheten.
$P(x)>0$ når $-3<x<1$ og $x>5$.
Løsningen kan også skrives som $x \in \langle -3,\,1 \rangle$ og $x \in \langle 5,\, \rightarrow \rangle$
Oppgave 4
a)
Differansen, d, mellom to ledd i en aritmetisk rekke er konstant. Finner d:
$a_4=a_1+d+d+d \\ 14=2+3d \\ 3d=12 \\ d=4$
| n | 1 | 2 | 3 | 4 | n |
| $a_n$ | 2 | 6 | 10 | 14 | |
| Formel | $2+4\cdot 0$ | $2+4\cdot 1$ | $2+4\cdot 2$ | $2+4\cdot 3$ | $2+4\cdot (n-1)=4n-2$ |
$a_n=4n-2$
b)
Summen av en aritmetisk rekke er gitt ved:
$S_n=\frac{a_1+a_n}{2} \cdot n$
Finner $a_{100}$:
$a_{100}=4\cdot 100-2=398$
Regner ut summen av de 100 første leddene i vår rekke:
$S_{100}=\frac{2+398}{2} \cdot 100 = 200 \cdot 100 = 20000$
Oppgave 5
a)
Dersom $-1<k<1$ i en geometrisk tallfølge $a_n=a_1k^{n-1}$ sier vi at den konvergerer. I slike tilfeller er $S_n=\frac{a_1}{1-k}$ når n går mot uendelig.
Her har vi $a_n=3\cdot (\frac{1}{4})^{n-1}$. Siden $-1<k<1$, så konvergerer rekken.
Regner ut summen av rekken når n går mot uendelig:
$S_n=\frac{3}{1-(\frac{1}{4})} = \frac{3}{\frac{3}{4}} = \frac{3\cdot 4}{3} = 4$
b)
$0,242424...=0,24+0,0024+0,000024+...=\frac{24}{100}+ \frac{24}{100^2}+\frac{24}{100^3}+...$
Dette er en geometrisk rekke hvor
$a_n=\frac{24}{100}\cdot (\frac{1}{100})^{n-1}$
Siden $-1<k<1$, konvergerer rekken. Summen av denne rekken når n går mot uendelig er:
$S_n=\frac{\frac{24}{100}}{1-\frac{1}{100}}=\frac{\frac{24}{100}}{\frac{99}{100}}=\frac{24}{99}$
Det betyr at $0,242424...$ kan skrives som $\frac{24}{99}$
Oppgave 6
a)
$f(x)=\frac{6}{1+e^{-x}}$
Bruker kvotientregelen for derivasjon.
$f'(x)=\frac{0 \cdot (1+e^{-x})-6 \cdot (-e^{-x})}{(1+e^{-x})^2} = \frac{6e^{-x}}{1+2e^{-x}+e^{-2x}}$
Alle potenser av $e$ er positive (og større enn 0). Både telleren og nevneren til $f'(x)$ er altså positive. En brøk med positiv teller og nevner har alltid positiv verdi. Altså er $f'(x)>0$ for alle verdier av x. Det vil si at $f(x)$ er strengt voksende.
b)
Finner grenseverdien av f(x) når x går mot uendelig:
$lim_{x \rightarrow \infty} e^{-x}=0$
Det vil si at når x går mot uendelig, går $e^{-x}$ mot null. Følgelig har vi at:
$lim_{x \rightarrow \infty} \frac{6}{1+e^{-x}}=\frac{6}{1+0}=6$
Finner grenseverdien av f(x) når x går mot minus uendelig:
$lim_{x \rightarrow - \infty} e^{-x}=e^{\infty}=\infty$
Det vil si at når x går mot minus uendelig, går $e^{-x}$ mot uendelig. Følgelig har vi at:
$lim_{x \rightarrow - \infty} \frac{6}{1+e^{-x}}=\frac{6}{\infty}=0$
Altså er $0<f(x)<6$.
c)
Bruker kvotientregelen for derivasjon.
$f ' '(x) = \frac{(-6e^{-x})(e^{-2x}+2e^{-x}+1)-(6e^{-x})(-2e^{-2x}-2e^{-x})}{(e^{-2x}+2e^{-x}+1)^2} \\ = \frac{-6e^{-3x}-12e^{-2x}-6e^{-x}+12e^{-3x}+12e^{-2x}}{(e^{-2x}+2e^{-x}+1)^2} \\ = \frac{6e^{-3x}-6e^{-x}}{(e^{-2x}+2e^{-x}+1)^2}$
Brøken kan forkortes videre, men vi behøver ikke det. Vi skal finne x-verdien hvor $f ' '(x)=0$, og trenger bare å se på telleren videre. Nevneren er et kvadrat av et uttrykk som alltid er større enn 0. Nevneren er derfor alltid større enn 0.
Vi har $f ' '(x)=0$ når $6e^{-3x}-6e^{-x}=0$.
$6e^{-3x}=6e^{-x} \\ e^{-3x}=e^{-x} \\ -3x=-x \\ x=0$
$f(x)$ har et vendepunkt i x=0. Finner y-verdien:
$f(0)=\frac{6}{1+e^{-0}}=\frac{6}{1+1}=3$
$f(x)$ har et vendepunkt i $(0,3)$.
d)
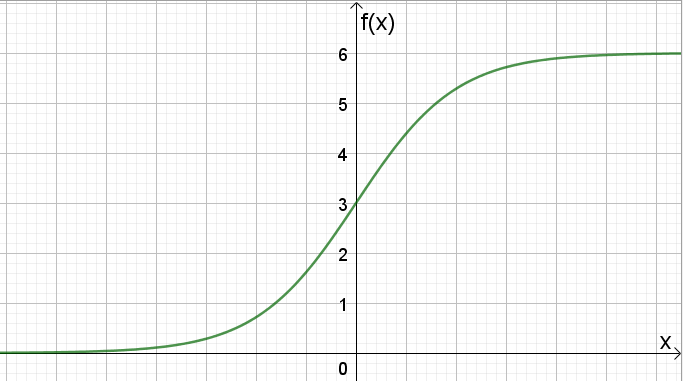
Vi vet at $0<f(x)<6$ og at vi har et vendepunkt i $(0,3)$. Vi vet også at dette er en logistisk funksjon, som er S-formet. Vi vet ikke så mye om x-aksen, men kunne eventuelt regne ut noen av punktene. Skisse av funksjonen:
Oppgave 7
a)
X er binomisk fordelt fordi:
- Vi har 10 delforsøk
- Det er to utfall i delforsøkene: $R$ eller $\overline{R}$ (rød kule eller ikke rød kule).
- $P(R)=\frac{6}{10}=\frac{3}{5}$. Det er lik sannsynlighet i alle delforsøkene, siden kulene legges tilbake etter hvert trekk.
- Delforsøkene er uavhengige av hverandre. Fargen på kulen du trekker i ett delforsøk, påvirker ikke fargen på kulen du trekker i neste delforsøk.
b)
$E(X)=n\cdot P(R)=10\cdot \frac{6}{10}=6$
$Var(X)=n\cdot P(R)\cdot (1-P(R))=10\cdot \frac{6}{10} \cdot \frac{4}{10}=\frac{24}{10}=2,4$
Oppgave 8
a)
$x=1,10 \Rightarrow z=\frac{x-\mu}{\sigma}=\frac{1,10-1}{0,05}=\frac{0,10}{0,05}=\frac{10}{5}=2$
$x=0,90 \Rightarrow z= \frac{0,90-1}{0,05}=\frac{-0,10}{0,05}=\frac{-10}{5}=-2$
$P(0,90 \leq X \leq 1,10)=P(-2 \leq Z \leq 2)=P(Z \leq 2)-P(Z \leq -2) = P(Z \leq 2)-(1-P(Z \leq 2)) \\ 0,97725-(1-0,97725) = 0,97725-0,02275=0,95450$
Sannsynligheten for at et tilfeldig valgt rugbrød veier mellom 0,90 kg og 1,10 kg er 95,45%.
b)
$\mu_S=n\cdot \mu_x=100\cdot 1,00\,kg=100\,kg$
$\sigma_S=\sqrt{n} \cdot \sigma_x=\sqrt{100}\cdot 0,05\,kg=10\cdot 0,05\,kg=0,5\,kg$
$S=100,5 \Rightarrow z=\frac{100,5-100}{0,5}=\frac{0,5}{0,5}=1$
$S=99,5 \Rightarrow z=\frac{99,5-100}{0,5}=\frac{-0,5}{0,5}=-1$
$P(99,5 \leq S \leq 100,5)=P(-1 \leq Z \leq 1)=P(Z \leq 1)- (1-P(Z\leq 1)) \\=0,84134-(1-0,84134)=0,84134-0,15866=0,68268$
Sannsynligheten for at veksten av rugbrødene på en tilfeldig pall er mellom 99,5 kg og 100,5 kg er ca. 68,3%.
Oppgave 9
$g(x)=-5 \cdot f(x)+3$
$g'(x)=-5\cdot f'(x)$. Det vil si at dersom $f'(x)=0$, så er $g'(x)=0$. $f(x)$ og $g(x)$ har derfor samme ekstremalpunkter. Derimot vil grafen til g synke når grafen til f stiger og omvendt, fordi $g'(x)$ alltid har motsatt fortegn som $f'(x)$.
Et toppunkt for $f$ er $(2,3)$. Det gir oss: $\\ g(2)=-5\cdot f(2)+3=-5\cdot 3+3=-15+3=-12$
Et bunnpunkt for $f$ er $(3,-4)$. Det gir oss: $\\ g(3)=-5\cdot f(3)+3= -5\cdot (-4)+3=20+3=23$
$g(x)$ har et bunnpunkt i $(2,-12)$ og et toppunkt i $(3,23)$.
DEL 2
Oppgave 1
a)
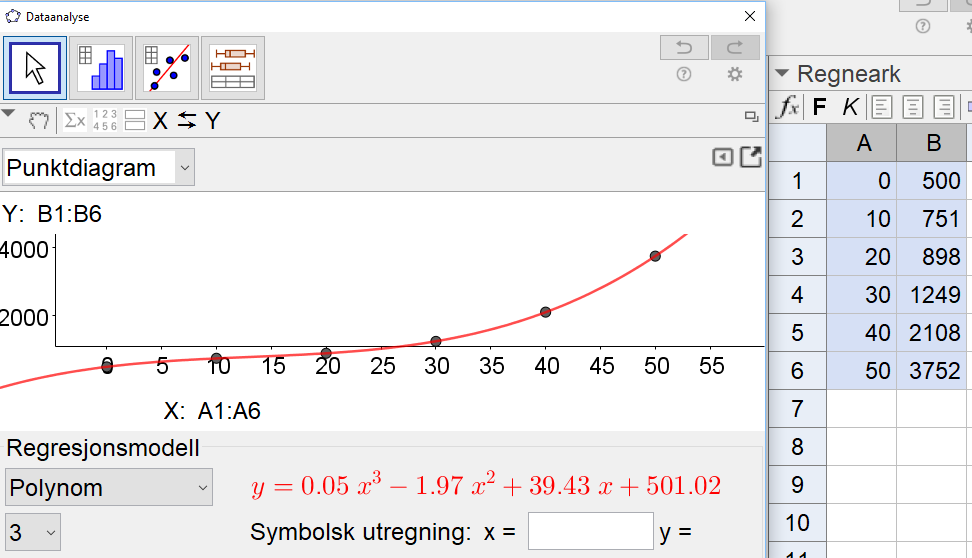
Bruker Geogebra til å utføre en regresjonsanalyse på punktene i tabellen. Velger polynomfunksjon av 3. grad som modell for kostnadene, h(x). Se skjermbildet under.
Jeg har funnet en modell for kostnaden, $h(x)=0,05x^3-1.97x^2+39,43x+501,02$
Inntekten er 80 kroner per enhet, og kan uttrykkes som $I(x)=80x$.
For å finne en modell for overskuddet, O(x), bruker jeg CAS i Geogebra, og regner ut O(x)=I(x)-h(x). Se skjermbildet under.
Jeg har dermed vist at funksjonen $O(x)=-0,05x^2+2,0x^2+41x-501$ (noe avrundet) er en god modell for det daglig overskuddet til bedriften ved produksjon av x enheter.
b)
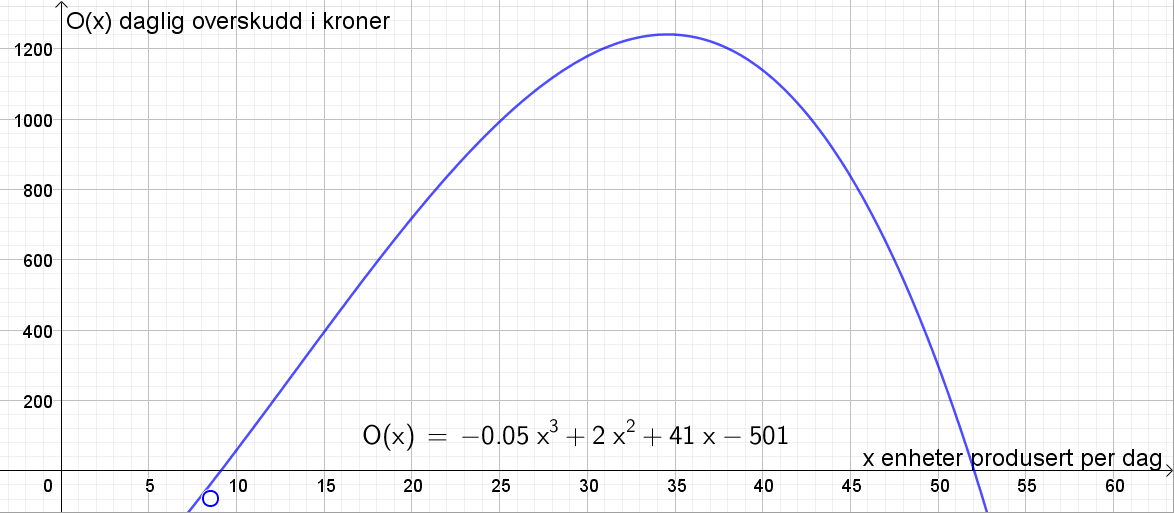
Tegner grafen til O i Geogebra.
c)
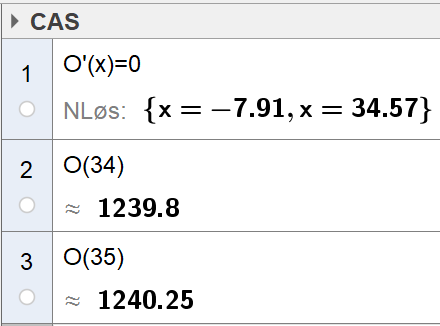
Når grensekostnaden er lik grenseinntekten, har vi det største overskuddet. Bruker CAS til å finne den daglige produksjonsmengden som gir størst overskudd (og altså grensekostnad lik grenseinntekt):
Ser av CAS (og grafen tegnet i b) at det er størst overskudd når x=34,57. Det er kun mulig å produsere et heltall antall varer. Sjekker derfor om det er 34 eller 35 antall varer produsert som gir det største overskuddet. Det viser seg at en daglig produksjon på 35 varer gir størst daglig overskudd.